Периметр и площадь – две основные характеристики геометрических фигур, которые имеют важное значение в различных задачах. Так, например, зная периметр прямоугольника, можно вычислить его площадь, а имея площадь треугольника, можно найти его периметр. Как же правильно найти периметр и площадь? В этой статье мы рассмотрим простые советы и примеры, которые помогут вам разобраться в этой теме.
Периметр – это сумма всех сторон фигуры. Чтобы найти периметр, необходимо просто просуммировать длины всех сторон. Например, для прямоугольника с длиной сторон a и b периметр будет равен P = 2a + 2b. Для квадрата со стороной a периметр вычисляется по формуле P = 4a.
Площадь – это количество плоскости, занимаемой фигурой. Найти площадь можно разными способами, в зависимости от фигуры. Например, площадь прямоугольника вычисляется как произведение длины и ширины, то есть S = a * b. Для квадрата площадь равна S = a * a.
В данной статье мы рассмотрели основные принципы вычисления периметра и площади различных геометрических фигур. Эти знания помогут вам в решении задач и повысят вашу математическую грамотность. Помните, что практика – лучший способ закрепить полученные знания, поэтому не забывайте решать задачи и примеры на нахождение периметра и площади.
Рассматриваемая задача

В этом разделе мы рассмотрим конкретную задачу, которая поможет нам лучше понять, как найти периметр и площадь фигур.
Представим, что у нас есть прямоугольник со сторонами 4 см и 6 см. Наша задача заключается в том, чтобы найти его периметр и площадь.
Периметр прямоугольника можно найти, сложив длины его всех сторон. В данном случае, у нас есть две стороны, каждая длиной 4 см, и две стороны, каждая длиной 6 см. Следовательно, периметр равен (4 + 4 + 6 + 6) = 20 см.
Площадь прямоугольника можно найти, умножив длину одной из его сторон на длину другой стороны. В данном случае, площадь равна (4 * 6) = 24 см².
Итак, периметр прямоугольника составляет 20 см, а его площадь равна 24 см².
В следующих разделах мы рассмотрим другие задачи и способы нахождения периметра и площади.
Постановка задачи и ее значимость

При решении задач по нахождению периметра и площади важно четко сформулировать постановку задачи. Постановка задачи должна содержать всю необходимую информацию о геометрической фигуре, для которой нужно найти периметр и площадь, а также об условиях, которые требуется выполнить при их нахождении.
Правильная постановка задачи позволяет точно определить, какие величины необходимо найти, какие формулы использовать и какие данные нужно вводить.
Задачи на нахождение периметра и площади имеют практическую значимость и применяются в различных областях деятельности. Например, в строительстве или проектировании, зная периметр и площадь земельного участка, можно рассчитать необходимое количество строительных материалов или определить стоимость строительных работ. В жизни также часто возникают ситуации, когда необходимо найти площадь или периметр фигуры, например, при покупке ковра или живой изгороди.
Умение решать задачи на нахождение периметра и площади является важным элементом математической грамотности и развивает логическое мышление. Овладение этими навыками поможет в дальнейшем успешно справляться с более сложными задачами и применять математические знания на практике.
Первый шаг: определение периметра
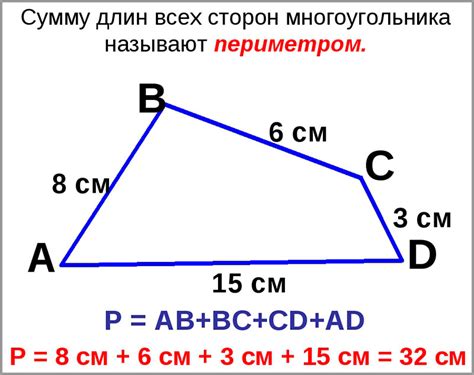
Для простых геометрических фигур, таких как прямоугольник или квадрат, периметр может быть рассчитан как удвоенная сумма всех сторон. Например, для прямоугольника со сторонами a и b, периметр будет равен 2(a + b).
Если у нас нет информации о сторонах фигуры, мы можем использовать координаты точек, чтобы определить периметр. Для этого нужно измерить расстояния между точками и сложить их. Например, для треугольника с вершинами A, B, C, периметр будет равен AB + BC + CA.
Важно помнить, что периметр измеряется в одних и тех же единицах длины, таких как сантиметры или метры.
Второй шаг: расчет площади

Для разных фигур существуют различные формулы расчета площади. Например, для квадрата площадь вычисляется как произведение длины стороны на саму себя. Для прямоугольника площадь равна произведению длины и ширины. Для треугольника формула более сложная, она зависит от известного нам ранее периметра и высоты. Для круга площадь вычисляется с помощью формулы, связывающей радиус и число Пи.
Для каждой фигуры необходимо знать соответствующие формулы и величины, которые мы вводим в них. Еще важно правильно провести измерения и записать их данные. В результате полученную площадь можно записать в нужной единице измерения, например в квадратных метрах или квадратных сантиметрах.
- Для квадрата: Площадь = сторона × сторона
- Для прямоугольника: Площадь = длина × ширина
- Для треугольника: Площадь = (основание × высота) / 2
- Для круга: Площадь = Пи × радиус²
Расчет площади фигуры можно проводить вручную, если известны все необходимые значения. Однако, в большинстве случаев можно воспользоваться калькулятором или формулами в специализированном программном обеспечении.
Зная площадь фигуры, мы получаем информацию о ее размере и площади покрытия. Эта величина может быть полезной при планировании различных задач, таких как укладка плитки, расстановка мебели или высадка растений. Площадь фигуры является важным параметром при анализе формы и размера объектов в геометрии, строительстве и других областях.
Простые советы для решения задачи

При решении задач на нахождение периметра и площади следует учитывать несколько важных моментов:
- Внимательно прочтите условие задачи и понимайте, что от вас требуется. Постройте схему или чертеж, если это поможет вам лучше понять поставленную задачу.
- Определите, какие значения известны в задаче и какие нужно найти. Обозначьте их символами или переменными. Это поможет вам лучше структурировать решение задачи.
- Используйте соответствующие формулы для нахождения периметра и площади. Для прямоугольника, например, периметр вычисляется по формуле:
P = 2(a + b), гдеaиb- длины сторон. - Правильно подставьте значения в формулы и выполните необходимые математические операции. Обратите внимание на единицы измерения, которые следует использовать в ответе.
- Проверьте полученный результат и убедитесь, что он логичен. Иногда бывает полезно провести дополнительные вычисления или сравнить ответ с другими известными значениями.
Следуя этим простым советам, вы сможете успешно решать задачи на нахождение периметра и площади, даже если у вас не очень сильное математическое образование.
Примеры задач с решениями

Вот несколько примеров задач, в которых нужно найти периметр и площадь:
Пример 1: Найдите периметр и площадь прямоугольника, если его стороны равны 5 и 8. Решение: Периметр прямоугольника равен удвоенной сумме его сторон: P = 2(5 + 8) = 26. Площадь прямоугольника равна произведению его сторон: S = 5 * 8 = 40. |
Пример 2: Найдите периметр и площадь квадрата, если его сторона равна 6. Решение: Периметр квадрата равен учетверенной длине его стороны: P = 4 * 6 = 24. Площадь квадрата равна квадрату длины его стороны: S = 6 * 6 = 36. |
Пример 3: Найдите периметр и площадь треугольника, если его стороны равны 3, 5 и 7. Решение: Периметр треугольника равен сумме его сторон: P = 3 + 5 + 7 = 15. Чтобы найти площадь треугольника, можно использовать формулу Герона: S = sqrt(p * (p - a) * (p - b) * (p - c)), где p - полупериметр треугольника, a, b, c - его стороны. В данном случае p = (3 + 5 + 7) / 2 = 7. Подставляя значения в формулу, получаем: S = sqrt(7 * (7 - 3) * (7 - 5) * (7 - 7)) = sqrt(7 * 4 * 2 * 0) = 0. |
Это лишь несколько примеров, но основные принципы решения задач на нахождение периметра и площади остаются неизменными. Решая подобные задачи, помните, что периметр - это сумма длин всех сторон фигуры, а площадь - это количество площадных единиц, занимаемых фигурой на плоскости.