Ромб - это особый вид четырехугольника, у которого все стороны равны. Принципиальной особенностью ромба является равенство их диагоналей, пересекающихся под прямым углом.
Для того чтобы найти периметр ромба, необходимо знать значение его одной стороны. Однако в данном случае нам даны две диагонали, их длины равны 10 и 12. Как же вычислить периметр ромба?
Для начала, находим длину стороны. Для этого воспользуемся формулой: сторона = √((диагональ1)2 + (диагональ2)2) / 2. В нашем случае: сторона = √((10)2 + (12)2) / 2. Вычисляем: сторона = √(100 + 144) / 2 = √244 / 2 ≈ 7.84.
Периметр ромба с диагоналями 10 и 12 - как найти известные значения длин диагоналей?
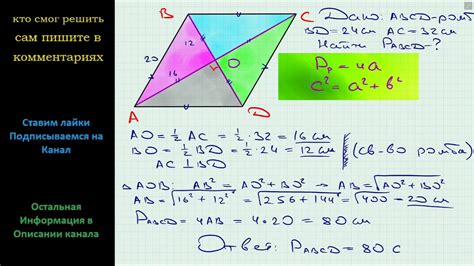
Для вычисления периметра ромба с диагоналями известной длины, необходимо знать значения длин обеих диагоналей. В данном случае, длины диагоналей равны 10 и 12.
Периметр ромба вычисляется по формуле:
P = 4a
где P - периметр ромба, a - длина стороны ромба.
Для ромба с диагоналями известной длины, длины стороны можно найти с помощью формулы:
a = \sqrt{\frac{d_1^2 + d_2^2}{4}}
где d_1 и d_2 - длины диагоналей ромба.
В нашем случае, длины диагоналей равны 10 и 12, поэтому вычисляем длину стороны:
a = \sqrt{\frac{10^2 + 12^2}{4}} = \sqrt{\frac{100 + 144}{4}} = \sqrt{\frac{244}{4}} = \sqrt{61}
Теперь, используя значение длины стороны ромба, вычисляем периметр:
P = 4 \cdot \sqrt{61} = 4 \cdot 7.81 \approx 31.24
Таким образом, периметр ромба с диагоналями 10 и 12 равен примерно 31.24.
Изучение основных свойств ромба
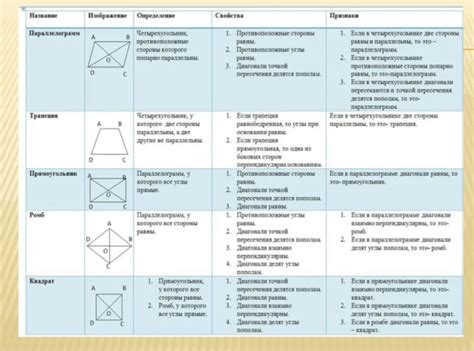
| Стороны: | Все стороны ромба равны друг другу. |
| Углы: | Все углы ромба равны между собой и составляют 90 градусов. |
| Диагонали: | Диагонали ромба перпендикулярны друг другу и делят его на четыре равные части. |
| Периметр: | Периметр ромба можно найти, складывая длины его четырех сторон. |
| Площадь: | Площадь ромба можно найти, используя формулу: площадь = (длина диагонали 1 * длина диагонали 2) / 2. |
Пользуясь данными основными свойствами ромба, мы можем рассчитать его периметр. Например, если заданы длины диагоналей ромба (10 и 12), мы можем использовать формулу для нахождения периметра, зная что каждая сторона ромба равна:
сторона = (длина диагонали 1 * длина диагонали 2) / (2 * √(длина диагонали 12 + длина диагонали 22))
После того, как мы найдем длину стороны ромба, просто умножим ее на 4, чтобы найти периметр.
Основная формула для расчета периметра ромба
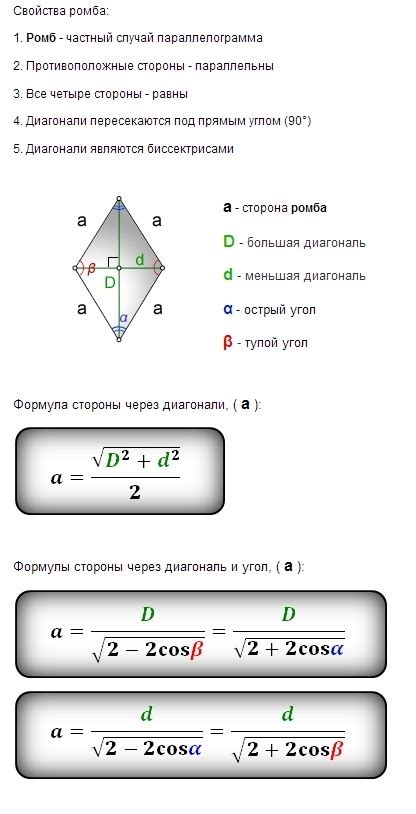
Периметр ромба может быть вычислен с использованием основной формулы, основанной на значениях его диагоналей:
Периметр ромба = 4 * a
где a - длина стороны ромба.
Так как ромб имеет все стороны равными, можно найти значение длины стороны ромба, зная его диагонали. Для этого нужно использовать следующую формулу:
a = sqrt((d1/2)^2 + (d2/2)^2)
где d1 и d2 - длины диагоналей ромба.
Известные значения длин диагоналей
Известные значения длин диагоналей ромба позволяют вычислить его периметр и другие характеристики.
В данном случае, даны длины двух диагоналей: 10 и 12. Используя эти значения, мы можем найти периметр ромба.
Расчет сторон ромба на основе известных диагоналей
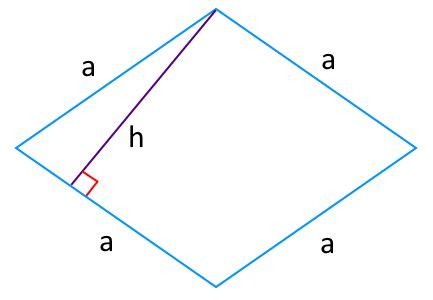
Для расчета сторон ромба на основе известных диагоналей можно использовать следующую формулу:
Сторона ромба равна половине произведения диагоналей, деленной на половину периметра.
Для заданного ромба с диагоналями 10 и 12, мы можем вычислить сторону следующим образом:
1. Найдите половину произведения диагоналей: (10 * 12) / 2 = 60.
2. Вычислите половину периметра ромба. Ромб имеет четыре одинаковые стороны, поэтому периметр можно найти как 4 * сторона. В данном случае, сторона = 60 / 4 = 15.
Таким образом, сторона ромба с диагоналями 10 и 12 равна 15.
Сложение длин сторон для нахождения периметра

В данном случае, у нас известны диагонали ромба, которые равны 10 и 12. Для нахождения периметра нам нужно найти длины его сторон по формуле:
Длина стороны = Диагональ / √2
Сначала найдем длины сторон по формуле:
Длина первой стороны = 10 / √2 = 7.07
Длина второй стороны = 12 / √2 = 8.49
Теперь, когда мы нашли длины всех сторон ромба, мы можем сложить их для нахождения периметра:
Периметр ромба = Длина первой стороны + Длина второй стороны + Длина первой стороны + Длина второй стороны = 7.07 + 8.49 + 7.07 + 8.49 = 31.12
Таким образом, периметр ромба с диагоналями 10 и 12 равен 31.12.
Пример расчета периметра ромба с диагоналями 10 и 12

Для расчета периметра ромба необходимо знать длины его сторон. Однако, при наличии информации о длинах диагоналей можно применить формулу, которая позволяет найти периметр ромба. В данном примере рассмотрим ромб, диагонали которого имеют длины 10 и 12.
Для начала, необходимо определить длины сторон ромба, используя длины диагоналей и свойство этой фигуры:
В ромбе диагонали являются взаимоперпендикулярными и делят его на 4 равных треугольника. Таким образом, каждая диагональ является высотой для одного из треугольников.
Для расчета длин сторон можно воспользоваться теоремой Пифагора. Пусть диагональ с длиной 10 является основанием треугольника, а другая диагональ с длиной 12 - высотой. Тогда:
| Длина основания (a): | 5 |
| Длина высоты (h): | 12 |
Рассчитаем длины оставшихся сторон ромба, зная длину основания и высоту:
| Длина стороны (b): | sqrt(a^2 + h^2) = sqrt(5^2 + 12^2) = sqrt(25 + 144) = sqrt(169) = 13 |
Таким образом, все стороны ромба имеют длину 13. Для расчета периметра ромба просто нужно сложить все его стороны:
| Периметр ромба: | 4 * b = 4 * 13 = 52 |
Таким образом, периметр ромба с диагоналями 10 и 12 составляет 52.