Круг - одна из наиболее известных и распространенных геометрических фигур. Изучение круга начинается с вычисления его площади, так как это одно из важных свойств этой фигуры. Площадь круга определяется по формуле, которая позволяет найти точное значение этой величины.
Формула для вычисления площади круга основана на радиусе, который является одним из ключевых параметров фигуры. Радиус - это расстояние от центра круга до любой точки на его окружности. Для вычисления площади круга необходимо знать значение радиуса.
Формула для вычисления площади круга выглядит следующим образом: S = π * r^2, где S - это площадь круга, π (пи) - это математическая константа, примерно равная 3.14159, а r - радиус круга. Чтобы найти площадь круга, нужно возведенить радиус в квадрат и умножить результат на π.
Площадь круга может быть выражена в квадратных единицах, таких как квадратные сантиметры или квадратные метры. Вычисление площади круга помогает определить, сколько пространства занимает эта фигура и может быть полезно в различных задачах, связанных с геометрией и изучением пространственных объектов.
Формула нахождения площади круга

Площадь круга можно вычислить с помощью простой формулы:
| S = | π * r2 |
где:
- S - площадь круга;
- π - математическая константа Pi, примерное значение равно 3.14159;
- r - радиус круга.
Обратите внимание, что радиус круга - это расстояние от центра круга до его любой точки на окружности.
Для использования данной формулы необходимо знать значение радиуса круга. Если радиус неизвестен, его можно определить, измерив расстояние от центра круга до любой точки на окружности с помощью линейки или другого подходящего инструмента.
Круг и его особенности
Для расчета площади круга используется математическая формула:
S = πr2
где S - площадь круга, π - математическая константа, приближенное значение которой равно 3,14, а r - радиус круга.
Зная значение радиуса, можно легко вычислить площадь круга по данной формуле. Это особенно полезно при проектировании и решении различных задач в области геометрии и физики.
Важно отметить, что площадь круга всегда положительна и измеряется в квадратных единицах длины, таких как квадратные сантиметры или квадратные метры.
Также следует обратить внимание, что круг имеет множество других характеристик, таких как диаметр, окружность и дуга, которые можно изучить более подробно.
Формула для вычисления площади круга
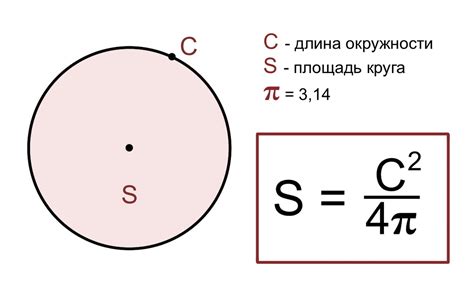
Формула для вычисления площади круга выглядит так:
- Шаг 1: Возьмите значение радиуса круга, обозначенное как "r".
- Шаг 2: Возведите значение радиуса в квадрат, умножив его на само себя. Полученное значение обозначается как "r²".
- Шаг 3: Умножьте значение "r²" на число "π" (пи), которое примерно равно 3,14159. Результат будет площадью круга.
Или можно использовать следующую формулу:
- Площадь круга = π * r²
Где "π" - это математическая константа, которую можно принять равной 3,14159 или округлить до 3,14.
Таким образом, чтобы найти площадь круга, необходимо знать его радиус и подставить значение в формулу. Полученный результат будет площадью круга в квадратных единицах.
Простое руководство по использованию формулы

Чтобы найти площадь круга, необходимо использовать следующую формулу:
Площадь круга = пи (π) * радиус * радиус.
1. Узнайте значение радиуса круга. Радиус - это расстояние от центра круга до любой точки на его окружности.
2. Возьмите значение радиуса и умножьте его само на себя - это означает возвести радиус в квадрат.
3. Возьмите число пи (π) - это математическая константа, приближенное значение которой равно 3,14159.
4. Умножьте число пи на квадрат радиуса, чтобы найти площадь круга.
Например, если радиус круга равен 4, то площадь круга будет:
Площадь = 3,14159 * 4 * 4 = 50,26544.
Итак, площадь круга с радиусом 4 равна примерно 50,27 квадратных единиц.
Теперь, используя эту формулу, вы сможете легко и быстро рассчитать площадь круга для любого заданного радиуса.