Квадрат - это геометрическая фигура, у которой все стороны имеют одинаковую длину и все углы прямые. Площадь квадрата можно найти, зная его периметр. Расчет площади - это важный элемент геометрии, который помогает нам определить площадь любой фигуры, в том числе и квадрата.
Определить площадь квадрата по периметру можно с помощью простой формулы. Для этого необходимо знать только значение периметра. Периметр квадрата равен сумме всех четырех его сторон, поэтому можно использовать следующую формулу: S = (P / 4)2, где S - это площадь квадрата, P - это периметр квадрата. Таким образом, зная значение периметра квадрата, мы можем легко найти его площадь.
Существует также несколько способов определения площади квадрата по периметру без использования формулы. Например, можно разделить квадрат на четыре треугольника, каждый из которых имеет сторону квадрата в качестве основания. Затем площади всех четырех треугольников можно сложить, и полученную сумму умножить на 2. Таким образом, мы также получим площадь квадрата. Это менее формулы, но эффективный способ определения площади квадрата по периметру.
Квадрат: определение и свойства
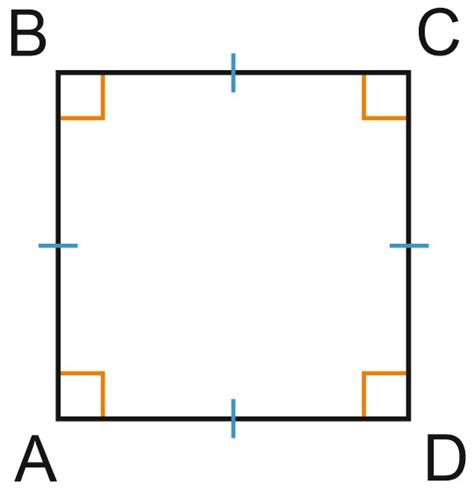
Основные свойства квадрата:
- Равные стороны: Все стороны квадрата имеют одинаковую длину.
- Прямые углы: Все углы квадрата равны 90 градусам.
- Диагонали: Диагонали квадрата являются радиусами его вписанной окружности. Диагонали также равны по длине и перпендикулярны друг к другу.
- Периметр: Периметр квадрата можно найти, умножив длину одной его стороны на 4.
- Площадь: Площадь квадрата можно найти, возведя в квадрат длину его стороны.
Квадрат - одна из основных геометрических фигур, которая обладает множеством уникальных свойств и широко используется в математике и строительстве.
Расчет площади квадрата по периметру
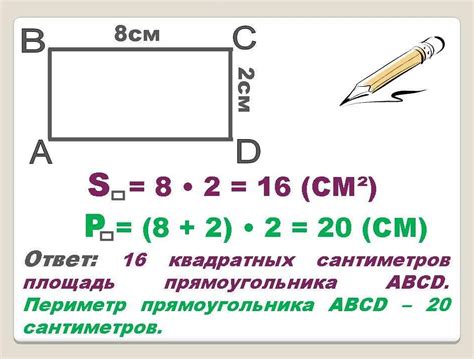
Первый способ использует простую формулу: площадь квадрата равна квадрату длины его стороны. Если известен периметр (P) квадрата, то можно найти длину его стороны (a) по формуле: a = P / 4. После этого можно найти площадь квадрата по формуле: S = a^2.
Второй способ основан на использовании высоты квадрата. Высота - это отрезок, проведенный между противоположными вершинами квадрата и перпендикулярный его сторонам. По известной высоте (h) можно найти площадь квадрата по формуле: S = h^2. Чтобы найти высоту квадрата, можно воспользоваться формулой: h = √(P^2 / 16).
Третий способ основан на использовании диагонали квадрата. Диагональ - это отрезок, соединяющий противоположные вершины квадрата. По известной диагонали (d) можно найти площадь квадрата по формуле: S = (d^2) / 2.
Используя эти способы, можно эффективно вычислить площадь квадрата по заданному периметру и потренироваться в решении геометрических задач.