Равнобедренный треугольник – это треугольник, у которого две стороны равны между собой, а третья сторона – основание – отличается от них. Высота равнобедренного треугольника – это перпендикуляр, опущенный из вершины на основание.
Чтобы найти площадь равнобедренного треугольника по высоте, необходимо знать длину основания и высоту. Формула для нахождения площади равнобедренного треугольника по высоте есть: S = (a * h) / 2, где S – площадь, a – длина основания, h – высота.
Чтобы взять удобный и понятный пример, представим равнобедренный треугольник со сторонами 5 см, 5 см и основанием 8 см. Чтобы найти высоту, нужно воспользоваться формулой h = sqrt(b^2 - (a/2)^2), где b – длина основания, a – длина равных сторон.
Что такое равнобедренный треугольник и высота треугольника?
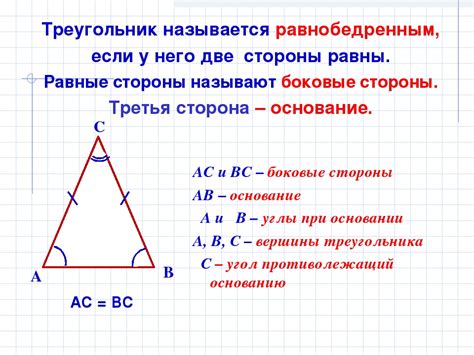
Высота треугольника - это отрезок, проведенный из вершины треугольника к прямой, содержащей противоположное основание. Она перпендикулярна основанию и образует прямой угол с основанием.
Для равнобедренного треугольника, проведенная из вершины к основанию высота делит треугольник на два прямоугольных треугольника, каждый из которых является половиной треугольника. Основание равнобедренного треугольника служит другим двум сторонам для поддержки, и их длины называются боковыми сторонами.
Равнобедренный треугольник может быть полным или развернутым. В полном равнобедренном треугольнике высота будет равна биссектрисе, разделяющей основание пополам и перпендикулярной ему, а основание будет являться отрезком между двумя точками пересечения основания и высоты. В развернутом равнобедренном треугольнике высота будет лежать вне треугольника и перпендикулярна основанию.
| Равнобедренный треугольник | Высота треугольника |
|---|---|
| A | B |
| /|\ | | |
| / | \ | | |
| / | \ | | |
| / |h \ | | |
| /_________\ | C |
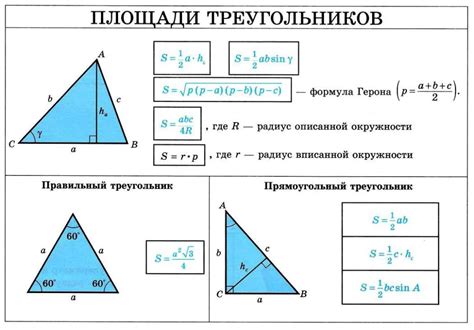
Понятие площади треугольника

Для равнобедренного треугольника площадь можно вычислить по формуле: S = (a*b)/2, где a - длина основания, b - длина высоты, опущенной на основание треугольника. Так как оба бедра равны, то основание можно считать любой стороной равнобедренного треугольника.
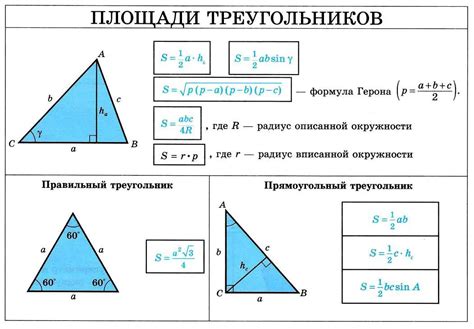
Существует также другая формула для нахождения площади треугольника - формула Герона. Она применима для треугольников любого вида, не только равнобедренных. Формула Герона выглядит следующим образом: S = √(p*(p-a)*(p-b)*(p-c)), где p - полупериметр треугольника, a, b, c - длины сторон треугольника.
Зная определение площади треугольника и умея применять соответствующие формулы, можно легко рассчитать площадь равнобедренного треугольника по его высоте.
Как вычислить площадь произвольного треугольника?
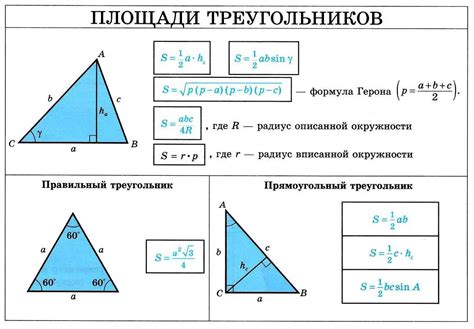
Площадь произвольного треугольника можно вычислить, зная длины всех его сторон или имея значения двух сторон и угла между ними. Вот два метода для вычисления площади:
1. Вычисление площади по длинам сторон
Если известны длины всех трех сторон треугольника (a, b и c), площадь можно вычислить по формуле Герона:
S = √(p(p - a)(p - b)(p - c))
где p - полупериметр треугольника, равный полусумме всех его сторон (p = (a + b + c) / 2).
2. Вычисление площади по двум сторонам и углу
Если известны длины двух сторон треугольника (a и b) и угол между ними (θ), площадь можно вычислить по формуле:
S = 0.5 * a * b * sin(θ)
Используя один из этих методов, вы можете легко вычислить площадь произвольного треугольника.
Формула для вычисления площади равнобедренного треугольника
Площадь равнобедренного треугольника можно вычислить, зная высоту, опущенную из вершины до основания, используя следующую формулу:
S = ½ * a * h |
Где:
S - площадь треугольника.
a - длина основания треугольника.
h - высота треугольника (расстояние от вершины до основания, опущенное перпендикулярно основанию).
Стало быть, чтобы найти площадь равнобедренного треугольника, необходимо умножить половину длины основания на высоту, проходящую из вершины до основания.
Обратите внимание, что помимо основания и высоты есть и другие методы вычисления площади равнобедренного треугольника, например, с использованием формулы Герона, если известны длины всех сторон треугольника.
Как найти высоту равнобедренного треугольника?
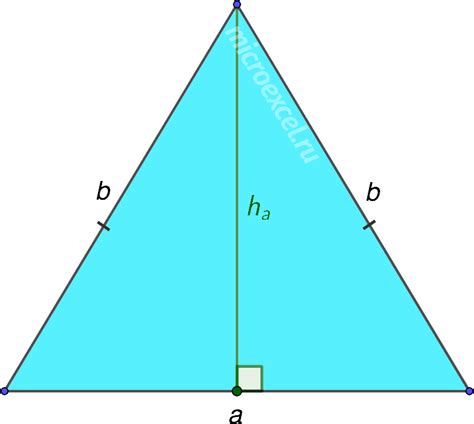
1. Зная основание и боковую сторону треугольника, можно вычислить высоту с помощью следующей формулы:
h = √(a2 - (b/2)2),
где h – высота, a – основание, b – боковая сторона.
2. Другой способ найти высоту равнобедренного треугольника – использовать свойство равнобедренности. Опустим высоту на основание треугольника – она разделит основание на две равные части и будет являться медианой. Зная медиану и основание, можно применить теорему Пифагора:
h = √(a2 - (b/2)2),
где h – высота, a – основание, b – боковая сторона.
Оба способа позволяют найти высоту равнобедренного треугольника, и выбор метода зависит от доступных данных. Используйте их в соответствии с условиями задачи.
Геометрическая конструкция для нахождения высоты треугольника
Для построения высоты равнобедренного треугольника выполните следующие шаги:
- Возьмите равнобедренный треугольник с вершиной В и основанием АС.
- Проведите биссектрису угла В треугольника ВАС.
- Пусть D - точка пересечения биссектрисы с основанием АС.
- Проведите прямую, проходящую через точку D и перпендикулярную основанию АС.
- Отрезок, соединяющий вершину В с точкой пересечения прямой с основанием АС - это высота треугольника.
После нахождения высоты равнобедренного треугольника можно использовать ее для вычисления площади треугольника. Для этого нужно умножить длину высоты на половину длины основания. То есть формула для нахождения площади равнобедренного треугольника будет выглядеть следующим образом: S = (1/2) * h * AC, где S - площадь треугольника, h - длина высоты, AC - длина основания треугольника.
Геометрическая конструкция для нахождения высоты равнобедренного треугольника позволяет легко решить задачу и получить необходимую информацию для нахождения площади треугольника. Этот метод является простым и эффективным, и может быть использован в школьной и профессиональной геометрии.
Формула для вычисления высоты треугольника
Существует несколько способов вычисления высоты треугольника:
| Метод | Формула |
|---|---|
| 1. С использованием площади треугольника | Высота (h) = (2 * Площадь треугольника) / Основание |
| 2. С использованием длины сторон треугольника | Высота (h) = (2 * Сторона) / Боковая сторона |
| 3. С использованием теоремы Пифагора | Высота (h) = √(Сторона^2 - (Основание/2)^2) |
Следуя одному из указанных методов, можно легко вычислить высоту равнобедренного треугольника и использовать ее для дальнейших необходимых расчетов, включая вычисление площади треугольника.
Как найти площадь равнобедренного треугольника по известной высоте?
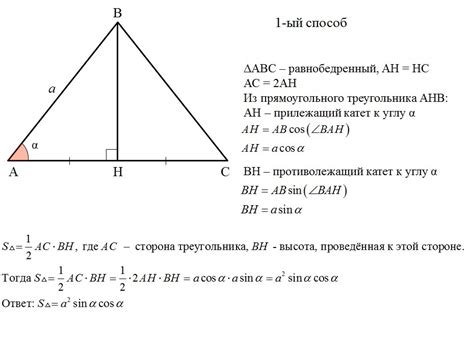
Площадь равнобедренного треугольника можно найти, используя известную высоту и одну из сторон треугольника. Для этого нужно следовать следующему алгоритму:
Шаг 1: Измерьте длину одного основания равнобедренного треугольника. Обозначим ее как "b".
Шаг 2: Измерьте длину высоты треугольника, которая опущена из вершины на основание. Обозначим ее как "h".
Шаг 3: Используя формулу для площади треугольника S = (b * h) / 2, вычислите площадь равнобедренного треугольника.
Пример:
Пусть основание треугольника равно 10 см, а высота равна 8 см.
Используя формулу S = (10 * 8) / 2, получаем:
S = 40 см²
Таким образом, площадь равнобедренного треугольника составляет 40 квадратных сантиметров.