Ромб – это четырехугольник, у которого все стороны равны между собой. Это особенная фигура, которая имеет свои уникальные свойства, в том числе и формулу для нахождения площади. На первый взгляд, может показаться, что нахождение площади ромба сложно, но на самом деле это довольно простая задача, особенно если ты учишься восьмом классе.
Формула для нахождения площади ромба опирается на его особенность – если провести диагональ ромба, то она разделит его на два равных прямоугольных треугольника. Зная длины диагоналей ромба, можно найти высоту, которая соединяет две противоположные вершины, и умножить ее на длину одной из диагоналей. После этого результат нужно умножить на два, так как площадь ромба состоит из двух таких треугольников.
Таким образом, формула для нахождения площади ромба выглядит следующим образом: S = d1 * h, где S – площадь ромба, d1 – длина одной из диагоналей, h – высота ромба. Обрати внимание, что формула для нахождения площади ромба не требует знания длин сторон, а только длин диагоналей, что делает задачу более простой.
Что такое ромб в геометрии
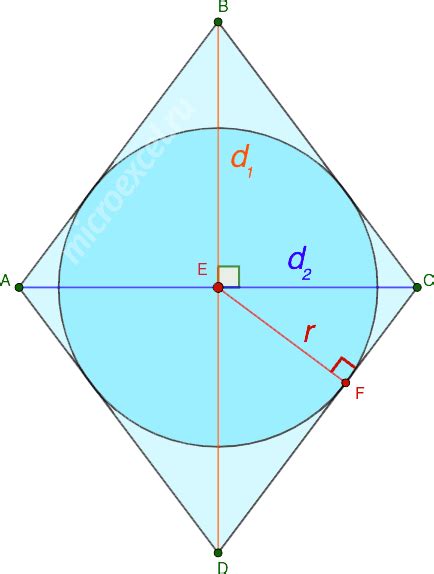
Ромб обладает несколькими характеристиками, которые делают его особенным:
- Все стороны ромба равны друг другу. Это значит, что если измерить любую сторону, то ее длина будет одинакова для всех сторон.
- Противоположные углы ромба равны друг другу. Все углы в ромбе равны 90 градусам, поэтому пара противоположных углов также будет равна.
- Диагонали ромба перпендикулярны друг другу. Диагонали - это отрезки, соединяющие две противоположные вершины ромба. Они пересекаются в точке, которая делит каждую диагональ пополам.
- Диагонали ромба делят его на четыре равных треугольника. Это означает, что площадь каждого из этих треугольников будет одинакова.
Площадь ромба можно найти, зная длины его диагоналей, используя специальную формулу. Ромб также имеет периметр, который можно найти, сложив длины всех его сторон.
Определение ромба и его свойства
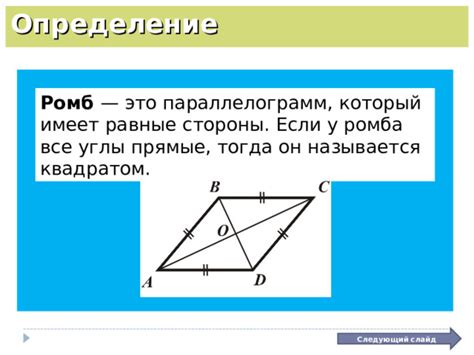
Основные свойства ромба:
- У ромба все стороны равны.
- У ромба все углы равны.
- Диагонали ромба перпендикулярны друг другу и делят его на 4 равных треугольника.
- Длины диагоналей ромба могут быть вычислены по формуле: d1 = a * sqrt(2), d2 = b * sqrt(2), где d1 и d2 - длины диагоналей, a и b - длины сторон ромба.
- Площадь ромба можно вычислить по формуле: S = (d1 * d2) / 2, где S - площадь ромба, d1 и d2 - длины диагоналей.
Формула для расчета площади ромба
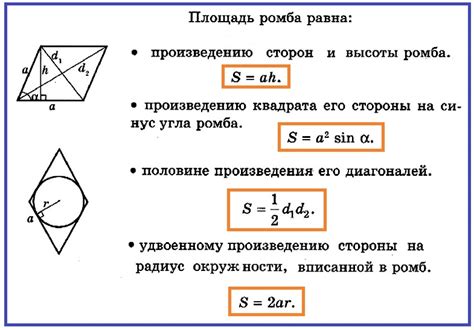
Площадь ромба можно вычислить, зная длину одной из его диагоналей и высоту, опущенную на эту диагональ.
Формула для расчета площади ромба:
- Найдите длину одной из диагоналей ромба.
- Умножьте длину диагонали на высоту, опущенную на эту диагональ.
- Разделите полученное произведение на 2.
Таким образом, формула для расчета площади ромба выглядит следующим образом:
Площадь = (Длина диагонали × Высота) / 2
Где длина диагонали и высота измеряются в одних и тех же единицах измерения.
Используя эту формулу, вы сможете легко вычислить площадь ромба с помощью известных значений длины диагонали и высоты.
Как найти длины диагоналей ромба

Длины диагоналей ромба можно найти, используя различные методы и формулы. Один из таких методов основан на свойствах ромба и его сторон.
Если известна длина одной стороны ромба, можно найти длину его диагоналей. Для этого можно воспользоваться следующей формулой:
Длина большей диагонали: D = a * √2
Длина меньшей диагонали: d = a * √2
Где a - длина одной стороны ромба.
Если не известна длина стороны ромба, но известны длины его диагоналей, можно воспользоваться формулой:
Длина стороны ромба: a = D / √2
Где D - длина большей диагонали ромба.
Также существует другой метод для нахождения длин диагоналей ромба, основанный на формуле Пифагора:
Длина большей диагонали: D = 2 * √(a2 + b2)
Длина меньшей диагонали: d = 2 * √(a2 + b2)
Где a и b - длины сторон ромба.
Теперь вы знаете различные методы для нахождения длин диагоналей ромба. Используйте их в зависимости от доступной информации.
Рассмотрение примера расчета площади ромба в 8 классе
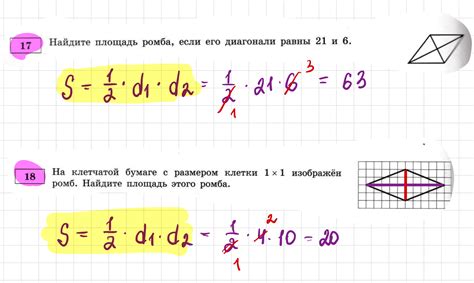
Давайте рассмотрим пример, чтобы лучше понять, как найти площадь ромба в 8 классе геометрии. Предположим, у нас есть ромб с диагоналями, равными 8 см и 6 см. Мы хотим найти его площадь.
1. В первую очередь, нужно вспомнить формулу для расчета площади ромба. Площадь ромба равна половине произведения диагоналей: S = (d1 * d2) / 2, где d1 и d2 - длины диагоналей.
2. В нашем случае, длина первой диагонали (d1) равна 8 см, а длина второй диагонали (d2) равна 6 см.
3. Подставим значения в формулу: S = (8 * 6) / 2 = 48 / 2 = 24 см².
4. Итак, площадь ромба равна 24 квадратных сантиметра.
Таким образом, мы рассмотрели пример расчета площади ромба с заданными диагоналями. Этот пример позволяет нам понять, как применить соответствующую формулу и получить ответ на задачу. Важно помнить, что формула для расчета площади ромба может быть использована в других задачах с ромбами.
Как вывести ответ в окончательной форме
Чтобы вывести ответ в окончательной форме, нужно убедиться, что все необходимые данные были правильно подставлены в формулу для нахождения площади ромба. Затем следует выполнить несложные математические операции и округлить полученное значение до нужного числа знаков после запятой.
Например, если говорится о нахождении площади ромба с диагоналями 10 см и 6 см, мы можем использовать формулу: площадь = (диагональ1 * диагональ2) / 2.
Подставив значения диагоналей в формулу, мы получим: площадь = (10 * 6) / 2 = 30 см².
Ответ можно представить в окончательной форме, указав единицы измерения и округлив до нужного числа знаков после запятой. В данном примере ответ будет выглядеть так: площадь ромба равна 30 см².