Трапеция - одна из самых распространенных геометрических фигур, которую мы встречаем в повседневной жизни. Но что делать, если нам неизвестна высота трапеции, а нужно найти ее площадь?
В этой статье мы рассмотрим несколько способов, как вычислить площадь трапеции без информации о высоте. Понимая принципы работы с данной фигурой, вы сможете самостоятельно решать подобные задачи без проблем!
Основной прием, который помогает найти площадь трапеции без использования высоты, основан на разбиении фигуры на несколько более простых элементов. Зная основания и боковые стороны трапеции, мы можем вычислить площади этих элементов и затем сложить их вместе.
Правила для расчета площади трапеции без высоты

1. Задайте значения оснований трапеции.
Первым шагом в расчете площади трапеции без высоты необходимо задать значения оснований. Основание трапеции - это боковые стороны, которые не являются параллельными. Обозначим их значения как "a" и "b" соответственно.
2. Измерьте длину боковой стороны трапеции.
Далее необходимо измерить длину боковой стороны трапеции, которая является перпендикулярной основаниям и устанавливается между ними. Обозначим значение этой стороны как "c".
3. Используйте формулу для вычисления площади.
Для расчета площади трапеции без высоты можно использовать формулу:
S = (a + b) * c / 2
4. Подставьте значения и рассчитайте площадь.
Подставьте значения оснований "a" и "b" и длину боковой стороны "c" в формулу и выполните необходимые вычисления. Полученное значение будет показателем площади трапеции без высоты.
5. Укажите единицы измерения площади.
Не забудьте указать единицы измерения площади в результате расчета. Результат может быть выражен в квадратных единицах, таких как квадратные метры или квадратные сантиметры.
Следуя этим правилам, вы сможете легко рассчитать площадь трапеции без высоты.
Выбор значения боковой стороны
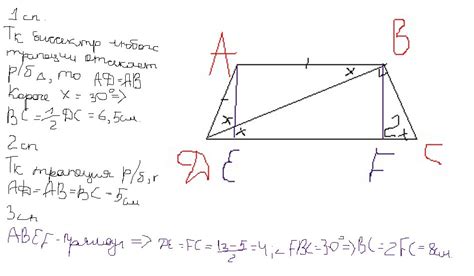
Если известны длины обеих боковых сторон трапеции, то для вычисления площади можно использовать любую из них. Это может быть полезно в случаях, когда требуется найти минимальную или максимальную площадь трапеции при заданных условиях.
Если известно лишь одно из значений боковых сторон, то для вычисления площади необходимо знать другие параметры, например, угол между боковыми сторонами или длину основания трапеции. В таком случае выбор значения боковой стороны будет зависеть от доступных данных и требований задачи.
При выборе значения боковой стороны следует учитывать, что длина основания трапеции должна быть больше нуля, а угол между боковыми сторонами должен быть острый, то есть меньше 90 градусов. В противном случае трапеция не будет существовать, и ее площадь будет равна нулю.
Нахождение длины оснований
1. Использование измерительных инструментов: Возьмите линейку или мерную ленту и измерьте длину каждого из оснований трапеции. Убедитесь, что вы измеряете правильно параллельные отрезки, а не диагонали или длины боковых сторон.
2. Использование известных данных: Если вам известны другие параметры трапеции, вы можете использовать их для нахождения длины оснований. Например, если известна площадь и высота трапеции, можно воспользоваться формулой для нахождения оснований:
- Площадь трапеции:
S = ((a + b) * h) / 2 - Где
aиb- длины оснований, аh- высота трапеции. - Решая данную формулу относительно одного из оснований, можно найти его значение.
3. Использование геометрических свойств: Если у вас есть информация о других углах и сторонах трапеции, можно воспользоваться геометрическими свойствами трапеции для нахождения длины оснований. Например, если трапеция является прямоугольной, то длины оснований равны длинам ее параллельных сторон.
Какой бы метод вы ни выбрали, важно обратить внимание на точность измерений и правильность вычислений, чтобы получить точные значения длин оснований трапеции.
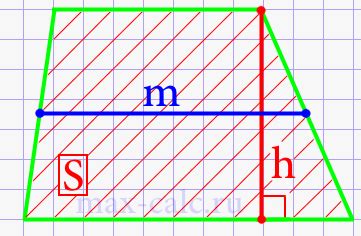
Рассчет средней линии

Средняя линия (m) = (a + b) / 2;
где a и b - длины боковых сторон трапеции.
Таким образом, для нахождения средней линии трапеции нужно сложить длины ее боковых сторон и разделить полученную сумму на 2.
Зная среднюю линию трапеции, вы сможете использовать ее для рассчета площади. Для этого достаточно знать длину средней линии (m), а также высоту (h) и формулу для площади трапеции без высоты:
Площадь трапеции без высоты (S) = m * h
Таким образом, с помощью знания средней линии и высоты, вы сможете рассчитать площадь трапеции без высоты, что может быть полезно в ряде задач и применений.
Использование формулы Герона

Формула Герона позволяет находить площадь трапеции без использования высоты. Для этого необходимо знать длины оснований и длину боковой стороны.
Применим формулу Герона для нахождения площади трапеции:
| Формула: | $S = \sqrt{(p - a)(p - b)(p - c)(p - d)}$, |
| где: | $p$ - полупериметр трапеции, |
| $a, b$ - длины оснований трапеции, | |
| $c$ - длина боковой стороны. |
Для вычисления полупериметра трапеции используется следующая формула:
| Формула: | $p = \frac{a + b + c + d}{2}$, |
| где: | $d$ - длина второй боковой стороны. |
После нахождения полупериметра трапеции, подставляем значения в формулу Герона и получаем площадь трапеции без использования высоты.
Важно помнить, что данная формула применима только для трапеций, у которых длины оснований и длина боковой стороны известны и соответствуют условиям трапеции.
Способы нахождения угла

При вычислении площади трапеции без высоты требуется знать значения всех углов фигуры. Углы трапеции могут быть найдены с помощью разных способов.
Один из способов - использование теоремы о сумме углов в многоугольнике. Согласно этой теореме, сумма всех внутренних углов в многоугольнике равна (n-2) × 180 градусов, где n - количество сторон многоугольника. Таким образом, для трапеции сумма внутренних углов будет равна (4-2) × 180 градусов, то есть 360 градусов. Используя эту информацию, углы трапеции могут быть найдены путем вычитания из 360 градусов известных углов.
Другой способ нахождения углов трапеции - использование свойств параллельных прямых и углов. Согласно свойствам трапеции, основания трапеции параллельны, а дополнительные углы (углы на противоположных концах оснований) равны. Найденные углы могут быть использованы для определения значений других углов.
Вычисление углов трапеции может также быть осуществлено с использованием геометрических построений и теорем. Этот метод может потребовать больше времени и тщательного анализа фигуры, но может также предложить более точные результаты.
Применение формулы синуса

Если у трапеции известны ее основания a и b, а также угол α между основаниями, то площадь трапеции можно найти, используя формулу синуса:
S = ((a + b) / 2) * h
где S - площадь трапеции, a и b - длины оснований, а h - высота, которую можно найти с помощью формулы:
h = (b - a) * sin(α)
Эти формулы основаны на том факте, что высота трапеции является перпендикуляром к основаниям и делит ее на два прямоугольных треугольника. Угол α можно найти, используя тригонометрические функции.
Таким образом, зная основания трапеции и угол между ними, можно применить формулы синуса для нахождения площади трапеции без необходимости знать ее высоту.
Примечание: формулы и подходы к нахождению площади трапеции могут различаться в зависимости от известной информации о фигуре.
Измерение длины параллельных сторон

Для вычисления площади трапеции без высоты необходимо знать длины ее параллельных сторон. Измерение длины этих сторон может быть произведено с использованием различных инструментов и методов. Вот несколько советов и приемов, которые помогут вам измерить длину параллельных сторон трапеции.
1. Линейка или метр
Самый простой и распространенный способ измерения длины сторон трапеции - использование обычной линейки или метра. Разместите линейку или метр параллельно каждой стороне и прочитайте измерение. Убедитесь, что инструмент применяется непосредственно к стороне без искажений или изгибов.
2. Лазерный измеритель
Для более точного измерения длины параллельных сторон трапеции можно использовать лазерный измеритель. Это электронное устройство излучает лазерный луч, который отражается от объекта и позволяет определить его расстояние. Наведите лазерный измеритель на каждую сторону трапеции и считайте отраженное расстояние на дисплее.
3. Планшет и специальные программы
Современные технологии предлагают также использовать специальные программы на планшете или смартфоне для измерения длин сторон трапеции. Установите подходящую программу, следуйте инструкциям и используйте планшет как виртуальную линейку или лазерный измеритель.
Важно помнить, что для получения точного результата необходимо измерять стороны трапеции с наибольшей точностью и повторять измерения несколько раз для проверки. Для более сложных и необычных форм трапеции вам может потребоваться применять более сложные методы измерения, такие как использование геометрической теории.
Методы нахождения угла наклона

1. Использование тригонометрии
Один из простых способов найти угол наклона - использовать тригонометрические функции. Для этого нужно знать длину оснований и высоты трапеции, а также угол между основаниями. С помощью формулы тангенса можно найти угол наклона.
2. Использование известных углов
Если известны другие углы трапеции, можно использовать их для определения угла наклона. Например, если заданы угол при основании и угол при боковой стороне, то сумма этих углов равна 180 градусов. Путем вычитания из 180 градусов известных углов можно найти угол наклона.
3. Использование геометрических свойств
Еще один способ определить угол наклона - использовать геометрические свойства трапеции. Например, угол наклона равен углу, образованному упором оснований на боковые стороны. Зная длины оснований и высоту, можно вычислить угол наклона с использованием геометрических формул и теорем.
4. Использование таблицы углов трапеции
В случае, когда имеются конкретные значения углов трапеции, можно обратиться к таблице углов, где собраны значения углов для разных длин оснований и высоты. Найдя значения углов в таблице, можно определить угол наклона.
| Длина основания | Высота | Угол наклона |
|---|---|---|
| 5 | 4 | 30° |
| 8 | 6 | 45° |
| 10 | 7 | 50° |
Используя один из этих методов, можно найти угол наклона трапеции и продолжить вычисление площади без необходимости знания высоты.
Развитие навыков геометрических построений

Чтобы развить навыки геометрических построений, следует сначала освоить базовые методы и приемы:
- Построение отрезка – самый простой способ начать знакомство с геометрическими построениями. Для этого нужно взять две точки и нарисовать прямую, проходящую через них.
- Построение перпендикуляра – перпендикулярные линии имеют особое значение в геометрии. Научитесь строить их, используя направляющие или циркуль и линейку.
- Построение параллельных линий – параллельные линии также играют важную роль в геометрии. Изучите различные методы и приемы для их построения.
- Построение треугольника – треугольники - одни из основных геометрических фигур. Изучите разные способы построения правильных и неправильных треугольников.
После освоения базовых методов, можно приступить к более сложным построениям, таким как круги, трапеции, параллелограммы и другие фигуры. Важно помнить, что каждое построение требует точности и внимания к деталям. Регулярные тренировки помогут вам развить навыки геометрических построений и стать опытным геометром.
Проверка полученного результата

После вычисления площади трапеции без высоты, рекомендуется провести проверку полученного результата. Для этого можно воспользоваться одним из следующих методов:
- Использовать формулу площади трапеции, которая включает в себя высоту. Если известна высота трапеции, можно просто подставить ее значение в формулу и сравнить полученный результат с предыдущим. Если значения совпадают, то вероятно результат вычислений без высоты верен.
- Сравнить результат с другими методами расчета площади трапеции без высоты. Если есть альтернативные способы вычисления, можно использовать их, чтобы убедиться в правильности полученного результата.
- Провести дополнительные измерения и вычисления, если это возможно. Например, если у вас есть доступ к реальной физической модели трапеции, можно измерить ее площадь с помощью специальных инструментов и сравнить с результатом вычислений без высоты.
Важно помнить, что результаты вычислений могут быть приближенными и иметь определенную погрешность, особенно при использовании методов, которые не учитывают высоту трапеции. Поэтому рекомендуется использовать разные методы проверки и сравнить результаты для более точного результата.