Одним из способов нахождения площади треугольника является использование известной высоты и одной стороны треугольника. Этот метод позволяет быстро и точно определить площадь треугольника без необходимости измерять все его стороны.
Формула для нахождения площади треугольника с известной высотой и стороной выглядит следующим образом:
S = (a * h) / 2,
где S - площадь треугольника, a - одна из сторон треугольника, h - высота треугольника, опущенная на эту сторону.
Приведем пример, чтобы лучше понять, как применять эту формулу на практике:
Пусть у нас есть треугольник с известной стороной a = 8 и высотой h = 6. Используя формулу для нахождения площади, мы можем рассчитать:
S = (8 * 6) / 2 = 48 / 2 = 24.
Таким образом, площадь треугольника равна 24 квадратных единиц. Этот метод позволяет быстро и эффективно рассчитать площадь треугольника с известной высотой и стороной без необходимости проводить сложные измерения и вычисления.
Что такое площадь треугольника?
Площадь треугольника зависит от его основания и высоты. Для треугольника с известной высотой и стороной можно использовать специальную формулу для расчета площади. Формула выглядит следующим образом:
Площадь = (Основание * Высота) / 2
В этой формуле Основание представляет собой длину одной из сторон треугольника, а Высота - перпендикуляр, опущенный из вершины противолежащего угла на основание.
Найдя значения основания и высоты треугольника, можно подставить их в формулу и вычислить площадь треугольника. Например, если основание треугольника равно 5 см, а высота равна 4 см, то площадь треугольника будет:
Площадь = (5 см * 4 см) / 2 = 10 см²
Итак, площадь треугольника - это важное понятие в геометрии, которое позволяет измерить его плоскую поверхность. Для треугольника с известной высотой и стороной можно использовать специальную формулу для расчета площади, которая основывается на значении основания и высоты. Освоив эту формулу, можно легко вычислить площадь треугольника и использовать это знание в различных задачах и ситуациях.
Понятие и значение площади треугольника

Понимание площади треугольника является важным и полезным как в школьной математике, так и в различных практических областях, включая строительство, архитектуру, графику и другие. Знание площади треугольника позволяет решать задачи, связанные с измерением площадей поверхностей, определением объемов и т.д.
Площадь треугольника можно вычислить разными способами, в зависимости от известных данных о треугольнике. Одним из методов расчета площади треугольника является использование известной высоты и длины одной из сторон треугольника.
Зная высоту и длину одной из сторон треугольника, можно воспользоваться простой формулой:
- Умножьте длину стороны треугольника на его высоту.
- Разделите полученное значение на 2.
Таким образом, площадь треугольника равна половине произведения длины одной из его сторон на высоту, опущенную на эту сторону.
Знание и использование этой формулы позволяет легко и быстро находить площадь треугольника, если известны его высота и длина одной из сторон.
Как найти площадь треугольника с известной высотой и стороной?
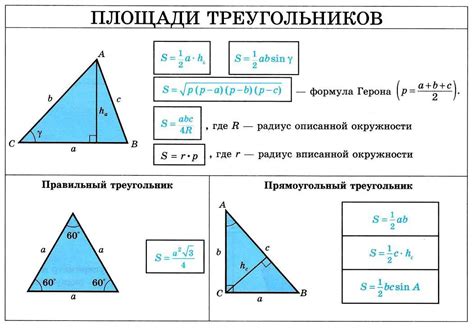
Площадь треугольника можно вычислить с помощью формулы, учитывающей известную высоту и одну из сторон треугольника. Формула для расчета площади треугольника:
S = (a * h) / 2
Где:
S - площадь треугольника;
a - длина одной из сторон треугольника;
h - высота, проведенная к стороне треугольника.
Для использования формулы достаточно знать длину одной из сторон и высоту, которая проведена к этой стороне.
Пример расчета:
Пусть треугольник имеет сторону длиной 4 см и высоту, проведенную к этой стороне, равную 3 см.
Применяя формулу, получим:
S = (4 * 3) / 2 = 6
Таким образом, площадь треугольника равна 6 квадратным сантиметрам.