Треугольник – это одна из наиболее простых геометрических фигур, но его площадь может быть довольно сложно вычислить. Особенно если мы не знаем углы и высоту треугольника. Однако существует простая формула, которая позволяет найти площадь треугольника зная длины всех его сторон.
Формула Герона, так называемая по имени греческого математика Герона Александрийского, позволяет вычислить площадь треугольника по его трем сторонам a, b и c. Формула имеет следующий вид:
Площадь = √(p * (p - a) * (p - b) * (p - c)),
где p – полупериметр треугольника, который вычисляется по формуле:
p = (a + b + c) / 2.
Теперь, когда вы знаете основную формулу и способ вычисления полупериметра, вы можете легко найти площадь треугольника по его трём сторонам. Это пригодится вам в решении различных геометрических задач или при нахождении площади треугольника на карте для пересчёта доли земной поверхности.
Как найти площадь треугольника по его 3 сторонам
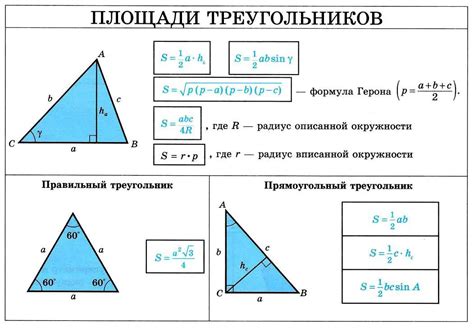
Формула Герона позволяет вычислить площадь треугольника, зная длины всех его сторон. Формула имеет следующий вид:
S = √(p * (p - a) * (p - b) * (p - c))
Где S - площадь треугольника;
a, b, c - длины сторон треугольника;
p - полупериметр треугольника, который вычисляется по формуле p = (a + b + c) / 2.
Чтобы найти площадь треугольника по его 3 сторонам, необходимо:
- Вычислить полупериметр треугольника по формуле p = (a + b + c) / 2, где a, b, c - длины сторон.
- Подставить значения сторон и полупериметра в формулу Герона: S = √(p * (p - a) * (p - b) * (p - c)).
- Вычислить квадратный корень полученного значения.
Теперь у вас есть инструкция, как найти площадь треугольника по его 3 сторонам. Просто следуйте указанным шагам, используя формулу Герона, и получите итоговое значение площади треугольника.
Что такое площадь треугольника?
Площадь треугольника можно вычислить, зная длины его трех сторон. Для этого применяются различные формулы, в зависимости от данных, которые имеются. Например, если известны длины всех трех сторон треугольника, можно использовать формулу Герона, которая основывается на полупериметре треугольника.
Однако в случае, если известны длины сторон и углы в треугольнике, можно использовать формулу площади треугольника через синус угла между сторонами. Эта формула основывается на соотношении площади треугольника и площади параллелограмма, построенного на этих сторонах.
Площадь треугольника играет важную роль в геометрии, а также во многих практических областях, например, при расчетах строительных объектов, изготовлении и дизайне предметов одежды и т.д.
Формула Герона для нахождения площади треугольника

Формула Герона выглядит следующим образом:
S = √(p * (p - a) * (p - b) * (p - c))
Где:
- S - площадь треугольника
- a, b, c - длины сторон треугольника
- p - полупериметр треугольника, который можно найти по формуле: p = (a + b + c) / 2
Применение формулы Герона позволяет найти площадь треугольника без необходимости знать его высоту или углы. Это делает эту формулу удобной и широко используемой в практических расчетах.
Шаги для расчета площади треугольника
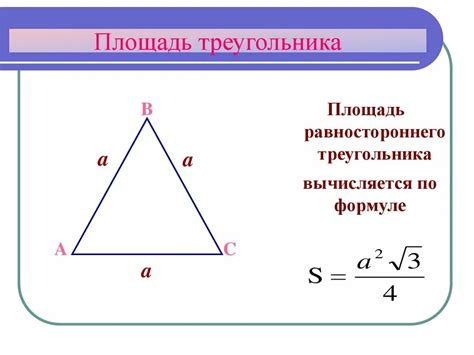
Расчет площади треугольника может быть выполнен с использованием формулы Герона, которая основывается на известных сторонах треугольника.
Шаги для расчета площади треугольника:
- Определите значения всех трех сторон треугольника.
- Используйте формулу Герона: S = sqrt(p * (p - a) * (p - b) * (p - c)), где S - площадь треугольника, p - полупериметр (p = (a + b + c) / 2), а a, b, c - стороны треугольника.
- Вычислите значение подкоренного выражения в формуле Герона и извлеките квадратный корень полученного значения.
- Полученный результат будет являться площадью треугольника.
Помните, что значения сторон треугольника должны быть положительными числами, а также сумма любых двух сторон треугольника должна быть больше третьей стороны.
Пример решения задачи

Предположим, у нас есть треугольник со сторонами a, b и c.
Сначала, мы можем найти полупериметр треугольника, который равен сумме всех сторон, деленной на 2:
периметр = (a + b + c) / 2
Затем, мы можем использовать формулу Герона для вычисления площади треугольника:
площадь = √(периметр * (периметр - a) * (периметр - b) * (периметр - c))
Итак, для нахождения площади треугольника по его сторонам, нам нужно выполнить следующие шаги:
- Найти полупериметр, используя формулу (a + b + c) / 2.
- Вычислить площадь, используя формулу √(периметр * (периметр - a) * (периметр - b) * (периметр - c)).
- Результатом будет площадь треугольника по его сторонам.
Применение этих шагов поможет нам находить площадь треугольника, зная его стороны.
Значение площади треугольника
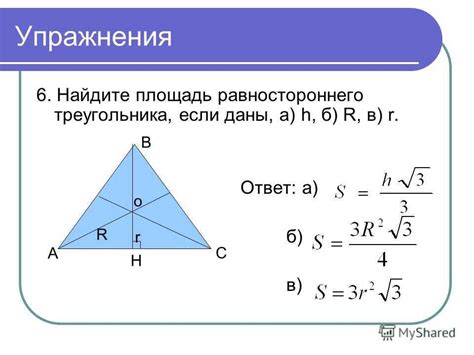
Формула Герона позволяет вычислить площадь треугольника, зная длины его сторон a, b и c. Она выглядит следующим образом:
S = √(p * (p - a) * (p - b) * (p - c)),
где p - полупериметр треугольника.
Значение площади треугольника может быть положительным или равным нулю. Если p * (p - a) * (p - b) * (p - c)
Площадь треугольника - это не только важная характеристика, но и используемое значение в различных областях применения, таких как строительство, графика, география и других.
Важность нахождения площади треугольника
Знание площади треугольника полезно для строителей, архитекторов и дизайнеров. Они используют эту информацию при проектировании и расчете материалов, например, для облицовки стен или кровли. Зная площадь треугольника, они могут точно определить количество необходимых материалов и просчитать бюджет проекта.
Площадь треугольника также играет важную роль в географии и навигации. Географы могут использовать эту информацию для определения размеров территорий или площади земельных участков. Навигационные карты и GPS-навигаторы также основываются на знании площади треугольника для определения расстояния между двумя точками и построения маршрутов.
Важность нахождения площади треугольника также связана с его геометрическими свойствами. Различные формулы для вычисления площади треугольника основываются на его сторонах и углах. Исследование этих формул и свойств треугольников позволяет расширить наши знания о геометрии и применить их в других областях математики.
Итак, нахождение площади треугольника имеет практическое значение в различных сферах деятельности и помогает нам лучше понять геометрию. Поэтому это важный навык, который стоит освоить для решения задач и применения в повседневной жизни.