Косвенные измерения – это метод, в котором значение измеряемой величины определяется на основе других измерений и уравнений. Они широко используются в физике, химии, инженерии и других науках. Однако при проведении косвенных измерений возникает неизбежная погрешность, связанная с погрешностью входных данных.
Умение вычислять погрешность косвенных измерений является важным навыком для любого исследователя или инженера. Она помогает оценить точность полученных результатов и предпринять соответствующие меры для минимизации погрешности.
Формула расчета погрешности косвенных измерений основана на методе дифференциалов, который позволяет учесть связь между величинами и их погрешностями. Погрешность k-й измеряемой величины (Δxk) вычисляется с помощью следующей формулы:
Δxk = sqrt((∂f/∂x1 * Δx1)^2 + (∂f/∂x2 * Δx2)^2 + ... + (∂f/∂xn * Δxn)^2),
где f - функция, связывающая измеряемые величины, x1, x2, ..., xn - измеряемые величины, Δx1, Δx2, ..., Δxn - погрешности измерений соответствующих величин.
Рассмотрим пример для наглядности. Предположим, мы хотим найти погрешность в рассчитанной площади S прямоугольника, используя размеры сторон a и b. Зависимость между величинами описывается формулой S = a * b. Если измерения a и b имеют погрешности Δa и Δb соответственно, то погрешность S будет вычислена в соответствии с формулой, приведенной выше.
Способы определения погрешности в косвенных измерениях

При выполнении косвенных измерений всегда существует погрешность, которая влияет на точность полученного результата. Чтобы корректно определить погрешность, можно использовать различные методы и формулы. Рассмотрим несколько наиболее распространенных способов.
1. Метод математических производных: данный метод основан на использовании производных величин, определяющих зависимость измеряемой величины от других физических величин. Используя формулу математических производных и известные значения погрешностей исходных величин, можно определить погрешность результата.
2. Метод линейного приближения: данный метод применяется, когда зависимость измеряемой величины от других физических величин является линейной. Используя формулу линейного приближения и известные значения погрешностей исходных величин, можно определить погрешность результата.
3. Метод законов сохранения: данный метод применяется, когда величины, которые влияют на результат измерения, подчиняются законам сохранения (например, закон сохранения энергии или закон сохранения импульса). Используя соответствующие законы сохранения и известные значения погрешностей исходных величин, можно определить погрешность результата.
4. Метод случайных величин: данный метод основан на использовании теории вероятностей и предполагает, что погрешность каждой измеряемой величины является случайной величиной. Используя формулы для расчета математического ожидания и дисперсии случайных величин, можно определить погрешность результата.
Каждый из этих методов имеет свои особенности и предназначен для определенных типов зависимостей исходных величин. При выборе метода необходимо учитывать конкретные условия и требования к точности измерений.
Зависимость погрешности от показателей точности измерительных приборов

При выполнении косвенных измерений необходимо учитывать точность используемых измерительных приборов, так как она оказывает непосредственное влияние на погрешность полученного результата.
Во-первых, следует обращать внимание на погрешность прибора, которая является одним из основных показателей его точности. Погрешность прибора указывается в его паспорте или технических характеристиках, и может быть выражена в процентах или абсолютных единицах.
Во-вторых, следует учитывать разрядность измерительного прибора, то есть количество знаков после запятой, которые он может показывать. Чем выше разрядность, тем более точные значения можно получить при измерении.
Также важно обратить внимание на цену деления прибора – это минимальное изменение величины, которое может быть определено при его использовании. Чем меньше цена деления, тем более точные измерения можно провести.
Применяя измерительные приборы с более высокими показателями точности (малой погрешностью, большей разрядностью и меньшей ценой деления), можно значительно снизить погрешность косвенных измерений и получить более точный результат.
Однако следует помнить, что точность измерительного прибора не является единственным фактором, влияющим на погрешность косвенных измерений. Важно также правильно оценить и учесть другие факторы, такие как систематические и случайные погрешности, а также правильно применять методы математической обработки результатов измерений.
Формула расчета погрешности для косвенных измерений

Погрешность при косвенных измерениях рассчитывается с использованием формулы пропагации погрешности. Эта формула позволяет оценить величину погрешности результата, полученного с использованием нескольких измерений и математических операций.
Формула пропагации погрешности имеет следующий вид:
ΔF = √((ΔA/A)^2 + (ΔB/B)^2 + ... + (ΔN/N)^2)
где ΔF - погрешность искомой величины F,
ΔA, ΔB, ... ΔN - погрешности измеренных величин A, B, ... N,
A, B, ... N - измеренные величины.
Формула позволяет учесть все вклады погрешностей отдельных измерений и учитывает их взаимное влияние на результат.
Рассмотрим пример:
Пусть нужно рассчитать площадь прямоугольника, измерив его стороны А и В. Погрешности измерений составляют ΔA = 0.1 см и ΔB = 0.2 см. Формула пропагации погрешности даст нам погрешность площади ΔS:
ΔS = √((ΔA/A)^2 + (ΔB/B)^2) = √((0.1/А)^2 + (0.2/B)^2)
Таким образом, зная погрешности измерений и значения самих измеренных величин, можно рассчитать погрешность результата и получить более точные и надежные результаты при косвенных измерениях.
Примеры расчета погрешности косвенных измерений
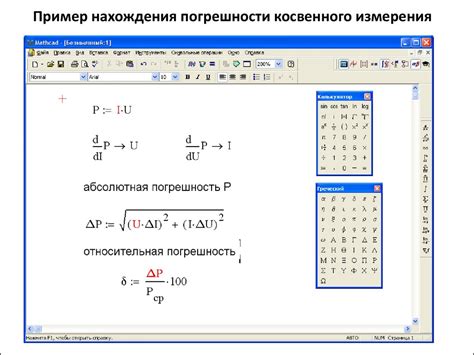
Для наглядности рассмотрим несколько примеров расчета погрешности косвенных измерений.
- Пример 1: Рассмотрим вычисление скорости движения автомобиля.
- Пример 2: Рассмотрим вычисление ускорения свободного падения на Земле.
Измеряемые значения: время движения – 10 с, расстояние – 100 м.
Среднее значение скорости, v = s/t = 100 м / 10 с = 10 м/с.
Погрешность времени, Δt = 0.1 с (погрешность измерительного прибора).
Погрешность расстояния, Δs = 1 м (погрешность измерительного прибора).
Погрешность скорости, Δv = v √((Δs/s)^2 + (Δt/t)^2).
Подставляя значения, получим Δv = 10 м/с √((1 м/100 м)^2 + (0.1 с/10 с)^2) ≈ 0.1 м/с.
Таким образом, скорость движения автомобиля составляет около 10 м/с с погрешностью примерно 0.1 м/с.
Измеряемые значения: время падения объекта – 2 с, высота падения – 20 м.
Ускорение свободного падения, g = 2h / t^2 = 2 * 20 м / 2^2 с^2 = 20 м/с^2.
Погрешность времени, Δt = 0.1 с.
Погрешность высоты падения, Δh = 0.5 м.
Погрешность ускорения свободного падения, Δg = g √((Δh/h)^2 + (2Δt/t)^2).
Подставляя значения, получим Δg = 20 м/с^2 √((0.5 м/20 м)^2 + (2 * 0.1 с/2 с)^2) ≈ 0.1 м/с^2.
Таким образом, ускорение свободного падения на Земле составляет около 20 м/с^2 с погрешностью примерно 0.1 м/с^2.
Ограничения и допущения при использовании формулы расчета погрешности

При использовании формулы расчета погрешности при измерении физических величин необходимо учитывать некоторые ограничения и допущения. Вот некоторые из них:
- Формула расчета погрешности предполагает линейную зависимость между измеряемой величиной и измерительной величиной. Если зависимость не является линейной, формула может давать неточные результаты.
- Формула не учитывает систематические ошибки измерений, такие как неправильная калибровка прибора или влияние окружающей среды на измерение. Для учета систематических ошибок необходимо применять дополнительные методы и формулы.
- Формула также предполагает независимость погрешности измеряемой величины от погрешности измерительной величины. В реальности эта зависимость может быть сложной и требовать дополнительного анализа.
- Формула не учитывает взаимное влияние различных источников погрешности. Если в измерении присутствуют несколько источников погрешности, их взаимное влияние может быть сложным и требовать более сложных формул и методов расчета.
При использовании формулы расчета погрешности необходимо быть внимательным к ограничениям и допущениям, чтобы получить точные и надежные результаты измерений. В некоторых случаях может потребоваться применение дополнительных методов и формул для более точного учета погрешности.