Конус - это геометрическое тело, которое имеет круглую основу и суживается к вершине, образуя поверхность в форме шапки шампанского. Расчет высоты конуса по его объему может быть необходим в различных ситуациях: от строительства до научных исследований.
Существует формула, позволяющая вычислить высоту конуса по его объему. Она основывается на математических свойствах данной геометрической фигуры и может быть применена в различных задачах.
Чтобы найти высоту конуса в зависимости от его объема, нужно воспользоваться следующим алгоритмом:
- Найдите формулу объема конуса. Она выглядит следующим образом: V = 1/3πr2h, где V - объем, π - число Пи (≈ 3,14159), r - радиус основания, h - высота конуса.
- Переставьте формулу так, чтобы искомая высота h стала единственной переменной: h = 3V / (πr2).
- Подставьте известные значения объема и радиуса основания в формулу и выполните необходимые математические операции.
- Полученное значение будет равно высоте конуса.
Найденная таким образом высота позволит более точно представить конус как геометрическое тело и использовать его параметры в необходимых расчетах и анализах.
Помните, что для корректного применения формулы необходимо использовать единицы измерения, соответствующие задаче, а также учитывать точность вычислений и округление результатов.
Как найти высоту конуса по объему: формула и алгоритм расчета
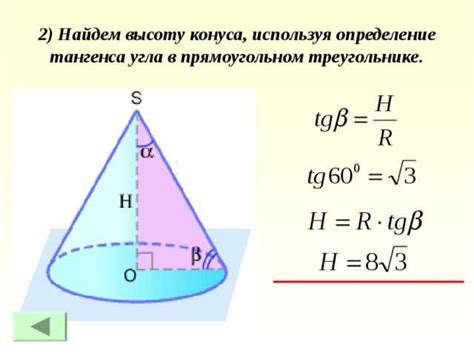
Формула для нахождения высоты конуса по его объему можно вывести, зная, что объем конуса определяется по формуле: V = (1/3) * π * R^2 * h, где V - объем конуса, π - число Пи (приблизительно равно 3.14159), R - радиус основания конуса, h - высота конуса.
Для нахождения высоты конуса по его объему следует следующий алгоритм:
- Исходя из известного значения объема V, выразить высоту h через радиус R.
- Раскрыть скобки в формуле объема конуса.
- Перенести все остальные члены уравнения на одну сторону и перегруппировать их.
- Произвести действия с переменными и числами.
- Найти корень из выражения при переменной h.
После того, как будет найдена высота конуса по его объему, можно использовать её для дальнейших расчетов или анализа геометрической фигуры.
Запомните, что решение задачи нахождения высоты конуса по его объему невозможно без использования соответствующей формулы и математических операций. Правильное применение алгоритма позволит получить точные значения и сэкономит время при решении подобных задач.
Методы определения высоты конуса по его объему
| Метод | Описание |
|---|---|
| Формула объема конуса | Используя формулу для подсчета объема конуса, можно выразить высоту как функцию от объема и радиуса основания. Формула для объема конуса: V = (1/3) * π * r2 * h, где V - объем, r - радиус основания, h - высота. Путем преобразования формулы можно получить h = (3 * V) / (π * r2). |
| Метод подразделения на две фигуры | Высоту конуса можно определить, разделив конус на две фигуры: конусный участок (truncated cone) и пирамиду с основанием, равным верхнему сечению конуса. После вычисления объема двух фигур и зная значения объема конуса и пирамиды, можно решить уравнение и определить высоту конуса. |
| Метод геометрической конструкции | С помощью геометрической конструкции и измерений можно определить высоту конуса. Для этого необходимо провести ось конуса и измерить расстояние от вершины конуса до основания. Это расстояние будет являться высотой конуса. |
| Метод численного решения | С использованием численных методов, таких как итерационные алгоритмы или методы оптимизации, можно численно определить высоту конуса по его объему. Для этого необходимо построить соответствующую функцию и найти её корень, который и будет являться искомой высотой конуса. |
Каждый из этих методов имеет свои преимущества и ограничения, и выбор конкретного метода зависит от задачи и доступных ресурсов.