Высота треугольника - важная характеристика, которая позволяет нам определить площадь фигуры. Но как же найти высоту треугольника к стороне? В этой статье мы рассмотрим несколько методов, которые помогут вам решить эту задачу.
Первый метод основан на использовании теоремы Пифагора. Итак, предположим, что у вас есть треугольник ABC, где сторона AC - основание, а точка H - высота, опущенная из вершины B на сторону AC. Тогда мы можем записать следующее уравнение: AC^2 = AH^2 + CH^2.
Другой метод основан на использовании площади треугольника. Если известна площадь треугольника ABC и длина одной из его сторон, то высоту можно найти с помощью следующей формулы: h = (2 * S) / a, где h - высота, S - площадь, a - длина стороны треугольника.
И наконец, третий метод основан на использовании подобия треугольников. Если треугольник ABC подобен треугольнику А1В1С1, и известны длины соответствующих сторон (например, AB и A1B1), то высота треугольника ABC к стороне AC будет равна произведению высоты треугольника A1B1C1 к стороне A1C1 на отношение длин сторон AB и A1B1.
Как измерить высоту треугольника?

Существует несколько методов для измерения высоты треугольника:
1. Использование формулы: Если известны длины сторон треугольника и длина одной из его высот, можно вычислить значение другой высоты, используя формулу:
Высота = (2 * Площадь треугольника) / Длина основания
2. Использование геометрической конструкции: Возьмите циркульную линейку и отметьте точку на основании треугольника. Затем, используя циркуль, измерьте расстояние от этой точки до вершины треугольника. Это и будет высотой треугольника.
3. Использование уровня или стержня: Возьмите уровень или стержень, который можно поставить вертикально. Установите его на основание треугольника и просто измерьте высоту треугольника с помощью шкалы на уровне или стержне.
4. Использование угломера: Если у вас есть угломер или проектор углов, можно заметить, что высота треугольника параллельна линии, проходящей через вершину треугольника и угол смежный с основанием.
Выберите подходящий метод измерения высоты, основываясь на доступных ресурсах и потребностях вашей задачи. Эти методы позволят вам точно измерить высоту треугольника и использовать эту информацию для решения различных математических задач.
Методика измерения высоты треугольника по одной из его сторон
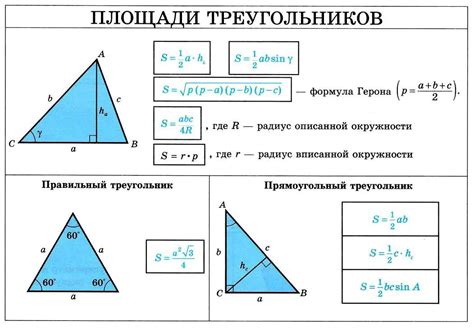
Для начала, необходимо определить, какая сторона треугольника будет использоваться для измерения высоты. Обозначим эту сторону как "a".
Шаги для вычисления высоты треугольника по одной стороне:
- Используя линейку или другой измерительный инструмент, измерьте длину стороны "a" треугольника.
- Найдите площадь треугольника по формуле: Площадь = (сторона "a" * высота) / 2.
- Выразите высоту из формулы, представленной на предыдущем шаге, получив: Высота = (2 * Площадь) / сторона "a".
Таким образом, вы можете определить высоту треугольника по известной стороне. Убедитесь, что используете корректные значения измерений и правильно применяете математические операции для получения точного результата.
Надеемся, что данная методика позволит вам успешно определить высоту треугольника по одной из его сторон.
Приближенное измерение высоты треугольника с помощью подобия
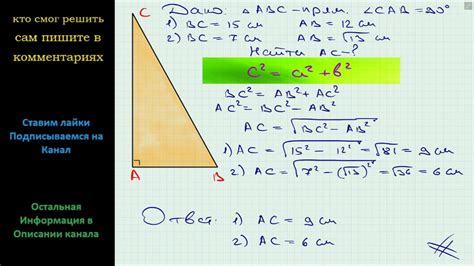
Алгоритм для приближенного измерения высоты треугольника заключается в следующем:
- Выберите одну из сторон треугольника, к которой вы хотите найти высоту. Обозначим ее как сторону А.
- Измерьте длину стороны А и запишите ее значение.
- Измерьте длину другой стороны треугольника и запишите ее значение. Обозначим ее как сторону В.
- С помощью подобия треугольников найдите соответствующие стороны другого треугольника.
- Измерьте длину соответствующей стороны второго треугольника и запишите ее значение. Обозначим ее как сторону С.
- Используйте пропорцию для определения высоты треугольника: высота = (длина стороны В * длина стороны А) / длина стороны С.
Чтобы лучше понять процесс приближенного измерения высоты треугольника с помощью подобия, рассмотрим пример:
| Треугольник ABC | Треугольник A'B'C' |
|---|---|
| AB = 6 см | A'B' = 4 см |
| BC = 8 см | B'C' = ? |
| AC = ? | A'C' = 6 см |
| Высота = ? | Высота = h см |
Применим пропорцию для определения высоты треугольника:
AB / BC = A'B' / B'C'
6 / 8 = 4 / B'C'
B'C' = (8 * 4) / 6
B'C' = 32 / 6 = 5,33 см
Таким образом, приближенная высота треугольника равна 5,33 см.
Используя метод приближенного измерения высоты с помощью подобия треугольников, можно получить достаточно точное приближение и упростить решение геометрических задач, когда точное измерение высоты треугольника невозможно или затруднительно.
Измерение высоты треугольника с использованием задачи о трёх перпендикулярах
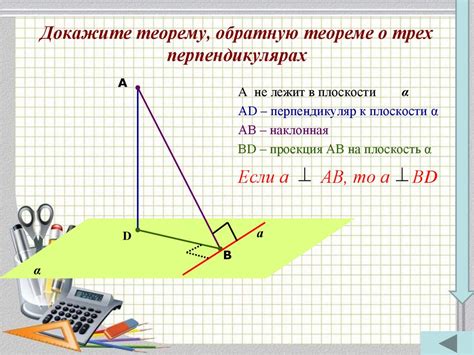
Одним из способов определить высоту треугольника является использование задачи о трёх перпендикулярах. В этой задаче находятся три перпендикуляра, соединяющие вершину треугольника с противоположными сторонами. Таким образом, получаются три прямоугольных треугольника, в которых одна из катетов - это сторона треугольника, а гипотенуза - высота треугольника.
Для измерения высоты треугольника с использованием задачи о трёх перпендикулярах, необходимо знать длины сторон треугольника. После этого, строятся перпендикуляры к сторонам треугольника, примыкающие к вершине, и находятся длины этих перпендикуляров.
Затем, используя теорему Пифагора для каждого из прямоугольных треугольников, находится длина высоты треугольника.
Измерение высоты треугольника с использованием задачи о трёх перпендикулярах является одним из методов, позволяющих найти высоту треугольника при известных длинах его сторон.
Как найти высоту равнобедренного треугольника?
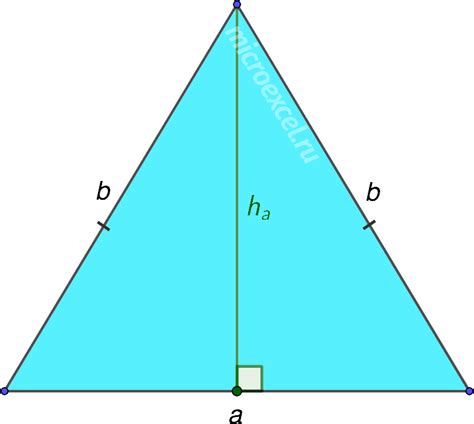
Существует несколько способов нахождения высоты равнобедренного треугольника:
- С помощью формулы: высота равнобедренного треугольника равна произведению основания и половины длины стороны, проведенной к высоте и параллельной основанию треугольника.
- Можно найти высоту, используя теорему Пифагора. Для этого необходимо разделить основание на два и найти длину отрезка, который является половиной основания. Затем, используя подобие треугольников, найденную длину можно использовать для нахождения высоты.
- Еще один способ - использовать теорему косинусов. Для этого нужно знать длину основания и угол при основании треугольника. Затем, используя формулу косинуса, можно вычислить длину высоты.
Выбор способа нахождения высоты равнобедренного треугольника зависит от доступных данных и уровня сложности задачи. Важно помнить, что высота равнобедренного треугольника является одной из ключевых характеристик этой геометрической фигуры и может использоваться для нахождения других параметров треугольника.
Как определить высоту треугольника с помощью формул Герона?

Формулы Герона позволяют находить площадь треугольника, зная длины его сторон. Одной из формул Герона является:
S = √(p * (p - a) * (p - b) * (p - c))
где S - площадь треугольника, p - полупериметр треугольника (p = (a + b + c) / 2), а a, b и c - длины сторон треугольника.
Для определения высоты треугольника с помощью формул Герона, можно использовать следующую формулу:
h = (2 * S) / a
где h - высота треугольника относительно стороны a, а S - площадь треугольника.
Следуя этим формулам, можно облегчить решение задачи нахождения высоты треугольника по заданным данным.
Примечание: необходимо знать длины всех сторон треугольника для использования формул Герона. Если изначально известна только длина одной стороны и некоторые другие данные (например, высота или угол), необходимо использовать другие методы для определения высоты треугольника.
Определение высоты треугольника с использованием теоремы косинусов
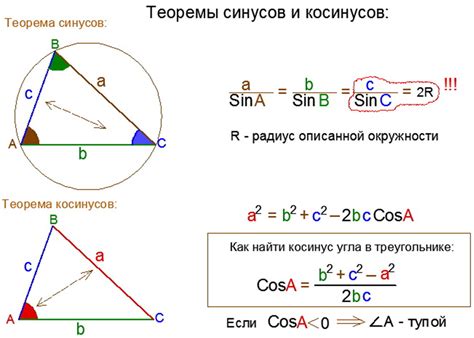
Для применения теоремы косинусов в определении высоты треугольника необходимо знать длины всех его сторон. Пусть треугольник имеет стороны a, b и c, а высота опущена на сторону c. Тогда можно воспользоваться следующей формулой:
h = sqrt(b^2 - ((a^2 + b^2 - c^2) / (2 * a))^2)
Где h - высота треугольника, a, b, c - длины его сторон.
Для использования этой формулы необходимо знать длины всех сторон треугольника. Эту информацию можно получить, измерив стороны с помощью линейки или построив треугольник по заданным координатам в декартовой системе.
Таким образом, используя теорему косинусов, можно определить высоту треугольника к стороне и добиться точных результатов при решении геометрических задач.
Как найти высоту треугольника, зная радиус вписанной окружности?

Теорема гласит, что высота треугольника, проведенная к стороне, равна произведению радиуса вписанной окружности на длину этой стороны и деленная на периметр треугольника:
h = (2 * r * a) / p
Где:
- h - высота треугольника;
- r - радиус вписанной окружности;
- a - длина стороны треугольника;
- p - периметр треугольника.
Используя данную формулу, можно легко и быстро найти высоту треугольника, если известен радиус вписанной окружности и длина одной из его сторон. Это может быть полезно при решении геометрических задач и вычислениях.
Как использовать площадь треугольника для нахождения его высоты?

Один из способов использования площади треугольника для нахождения его высоты - это использование формулы, связывающей площадь, основание и высоту треугольника:
| Формула | Обозначения |
|---|---|
| Площадь треугольника | S |
| Основание треугольника | b |
| Высота треугольника | h |
Формула высоты треугольника выглядит следующим образом:
h = (2 * S) / b
Где S - площадь треугольника, b - основание треугольника, h - высота треугольника.
Чтобы использовать эту формулу, необходимо знать площадь треугольника и длину его основания. Зная эти значения, вы можете вычислить высоту треугольника.
Обратите внимание, что эта формула работает только для обычных треугольников. Для треугольников, которые могут быть равнобедренными или прямоугольными, формулы для нахождения высоты будут отличаться. Для таких случаев лучше использовать другие методы или формулы.
Использование площади треугольника вместе с формулой для нахождения его высоты может быть полезным при решении геометрических задач и определении различных параметров треугольника. Этот метод может быть особенно полезен, если известна площадь треугольника и требуется найти его высоту без дополнительной информации.