Узнать, является ли число простым, является распространенной задачей в программировании. Простое число - это натуральное число, большее единицы, которое делится только на себя и на единицу без остатка. В этой статье мы рассмотрим, как проверить число на простоту, используя рекурсию в Python.
Использование рекурсии для проверки числа на простоту позволяет нам разделить задачу на более простые подзадачи и решить их последовательно. Мы будем рекурсивно проверять, делится ли число на каждое из чисел от 2 до корня из этого числа. Если мы находим делитель, число не является простым, иначе число является простым.
Рекурсивный подход к проверке числа на простоту в Python не только помогает в решении данной задачи, но и демонстрирует мощь рекурсии в программировании. Теперь давайте рассмотрим подробности реализации этого подхода и посмотрим, как он работает.
Что такое простое число?

Например, числа 2, 3, 5, 7, 11, 13, 17 и так далее являются простыми числами, так как они не имеют делителей, кроме 1 и самих себя. Однако числа, такие как 4, 6, 8, 9, 10 и т.д., не являются простыми числами, так как они имеют делители помимо 1 и себя.
Простые числа играют важную роль в теории чисел и имеют множество приложений в криптографии, математическом моделировании и других областях.
Простые числа в математике

Простые числа являются основой для множества математических теорем и алгоритмов. Они применяются в различных областях, таких как криптография, теория чисел, комбинаторика и многих других.
Нахождение простых чисел является одной из актуальных задач в математике. Существует множество методов и алгоритмов для определения простоты числа. Одним из простых и популярных методов является "метод перебора делителей". Этот метод позволяет проверить все числа от 2 до квадратного корня исследуемого числа, и если среди этих чисел нет делителей, то число считается простым.
Для более эффективной проверки числа на простоту можно использовать рекурсию. Рекурсивный алгоритм может проверить все числа от 2 до квадратного корня исследуемого числа, и в случае отсутствия делителей считать число простым.
| Пример простых чисел: | Не являются простыми числами: |
|---|---|
| 2 | 1 |
| 3 | 4 |
| 5 | 6 |
| 7 | 8 |
| 11 | 9 |
Простые числа являются важным объектом исследования в математике и имеют множество интересных свойств и приложений. Изучение простых чисел способствует расширению наших знаний о числах и позволяет решать сложные математические проблемы.
Алгоритм проверки числа на простоту

Простым числом называется натуральное число, которое больше единицы и имеет только два делителя - единицу и само число. Например, числа 2, 3, 5, 7, 11 являются простыми.
Алгоритм проверки числа на простоту может быть реализован различными способами. Один из таких способов - это проверка, является ли число делителем только для чисел из диапазона от 2 до квадратного корня из числа.
Для начала, необходимо проверить, является ли число равным 2. Если да, то число считается простым. Иначе, проверяем, является ли число четным. Если число - четное, то оно точно не является простым; в противном случае, продолжаем проверку.
Затем, начиная с числа 3, проверяем, есть ли у числа делители из диапазона от 2 до квадратного корня из числа. Если найдется делитель, то число считается составным; в противном случае, число считается простым.
Использование алгоритма проверки числа на простоту рекурсией позволяет многократно повторять проверку числа на делители, пока не будет найден делитель или не будет достигнут крайний диапазон для проверки. Это позволяет эффективно определить, является ли число простым.
Рекурсия в программировании

Основная идея рекурсии заключается в разделении задачи на более простые подзадачи таким образом, чтобы каждая подзадача была аналогична исходной задаче, но с меньшими размерами. Функция вызывает саму себя с новыми значениями, и таким образом, задача сокращается до более простых случаев, пока не будет достигнуто базовое условие, после чего начнется возврат обратно по стеку вызовов.
Рекурсивные функции обычно имеют две части: базовый случай и рекурсивный случай. Базовый случай определяет условие, при котором функция прекращает вызывать себя и начинает возврат. Рекурсивный случай определяет, как функция вызывает саму себя для решения более простой подзадачи.
Рекурсия может быть очень полезной при решении задач, где задача разбивается на меньшие подзадачи одинаковой структуры. Однако при неправильном использовании рекурсия может привести к бесконечным циклам и переполнению стека вызовов.
В Python рекурсия легко реализуется, поскольку язык поддерживает вызов функции из самой себя. Тем не менее, важно следить за базовым случаем и соблюдать правила остановки рекурсии, чтобы избежать проблем с производительностью и переполнением стека вызовов.
Что такое рекурсивная функция?

Принцип работы рекурсивной функции основан на итерационном процессе. То есть функция вызывается несколько раз, каждый раз решая более простую задачу. После каждого вызова функция передает часть работы следующему вызову, пока задача не станет настолько простой, что может быть решена без вызова самой функции.
Одним из примеров использования рекурсивной функции является проверка числа на простоту. Рекурсивная функция может проводить различные проверки для определения, является ли число простым или составным, пока не достигнет наименьшего возможного определения.
Рекурсивные функции могут быть очень эффективными, но также могут создавать проблемы, если они вызываются слишком много раз или без достаточного ограничения. Использование рекурсии требует внимательного планирования и тестирования, чтобы избежать зависаний и переполнения стека.
| Преимущества рекурсивных функций | Недостатки рекурсивных функций |
|---|---|
|
|
Рекурсивная проверка числа на простоту в Python
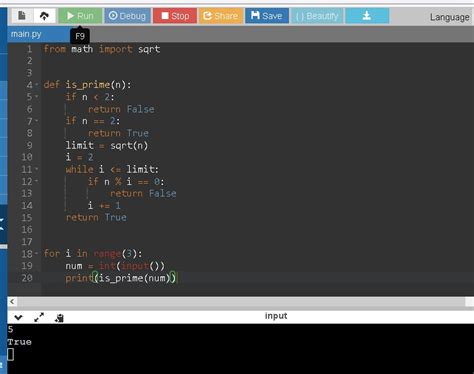
В этой статье мы рассмотрим рекурсивный способ проверки числа на простоту в языке программирования Python.
Простое число - это число, которое делится только на единицу и на само себя без остатка. Для проверки числа на простоту, мы будем использовать рекурсивную функцию, которая будет проверять, делится ли число на все числа от 2 до корня из этого числа.
Вот пример реализации функции для рекурсивной проверки числа на простоту в Python:
def is_prime(n): if n return False for i in range(2, int(n ** 0.5) + 1): if n % i == 0: return False return True В данной функции мы вначале проверяем случай, когда число меньше 2, так как 0 и 1 не являются простыми числами.
Затем мы пробегаем по всем числам от 2 до корня из заданного числа и проверяем, делится ли оно на которое-либо из них без остатка.
Если число делится хотя бы на одно число без остатка, то оно не является простым и функция возвращает False.
Если число не делится на ни одно число от 2 до корня из него, то оно является простым и функция возвращает True.
Мы можем вызвать данную функцию и проверить различные числа на простоту.
is_prime(7) # True
is_prime(10) # False Если мы хотим проверить диапазон чисел на простоту, мы можем использовать цикл и вызывать функцию для каждого числа, передавая его в качестве аргумента.
for number in range(1, 11): if is_prime(number): print(f"{number} - простое число") else: print(f"{number} - не простое число") Используя рекурсивную функцию для проверки числа на простоту, мы можем осуществлять эффективные вычисления и достигнуть требуемого результата.