Квадратные уравнения являются одним из основных инструментов алгебры и находят применение во многих областях науки и техники. Решение квадратного уравнения может быть осуществлено с помощью различных методов, но разработка эффективного алгоритма играет важную роль в оптимизации времени выполнения программы.

Python предлагает мощные инструменты для решения квадратных уравнений, которые позволяют быстро и точно находить все корни. В этой статье мы рассмотрим эффективный алгоритм решения квадратных уравнений в Python и приведем несколько примеров его применения.

Основная идея алгоритма состоит в использовании формулы дискриминанта для определения количества корней и их значений. При этом важно учесть возможные особые случаи, такие как отсутствие действительных корней или наличие кратных корней. Python обладает богатым набором математических функций и операторов, которые позволяют легко реализовать этот алгоритм и получить точные результаты.

Решение квадратного уравнения в Python

Существуют формулы, называемые формулами Виета, которые позволяют найти корни квадратного уравнения. Они основаны на сумме и произведении корней. Если у нас есть квадратное уравнение ax^2 + bx + c = 0, то его корни можно найти следующим образом:

• Найдем дискриминант D = b^2 - 4ac;
• Если D > 0, то уравнение имеет два различных корня x1 и x2, которые находятся по формулам: x1 = (-b + sqrt(D))/(2a) и x2 = (-b - sqrt(D))/(2a);
• Если D = 0, то уравнение имеет один корень x, который находится по формуле: x = -b/(2a);
• Если D

Приведем пример решения квадратного уравнения в Python с помощью указанного алгоритма:

def solve_quadratic_equation(a, b, c):
discriminant = b**2 - 4*a*c
if discriminant > 0:
x1 = (-b + discriminant**0.5) / (2 * a)
x2 = (-b - discriminant**0.5) / (2 * a)
return x1, x2
elif discriminant == 0:
x = -b / (2 * a)
return x
else:
return "No real roots"
# Пример использования функции
a = 1
b = -3
c = 2
solution = solve_quadratic_equation(a, b, c)
print(solution)

В данном примере мы решаем квадратное уравнение x^2 - 3x + 2 = 0. В результате выполнения программы, получим ответ (1, 2), что соответствует двум действительным корням уравнения.

Таким образом, решение квадратного уравнения в Python с использованием эффективного алгоритма дает возможность находить корни уравнения в зависимости от значения дискриминанта.

Эффективный алгоритм решения

Один из самых распространенных алгоритмов решения квадратного уравнения в Python основан на дискриминанте.

Для начала, необходимо вычислить значение дискриминанта по формуле: D = b^2 - 4ac. Здесь, a, b и c - коэффициенты квадратного уравнения.

После этого, можно проверить несколько условий:

1. Если D больше нуля, то у уравнения два корня.
2. Если D равно нулю, то у уравнения один корень.
3. Если D меньше нуля, то у уравнения нет корней.

Далее, можно вычислить значения корней, если они есть:

1. Если D больше нуля, то корни вычисляются по формулам: x₁ = (-b + √D) / (2a) и x₂ = (-b - √D) / (2a).
2. Если D равно нулю, то корень вычисляется по формуле: x = -b / (2a).

Таким образом, использование эффективного алгоритма на основе дискриминанта позволяет быстро и правильно решить квадратное уравнение в Python, сэкономив время и ресурсы компьютера.

Примеры решения квадратного уравнения

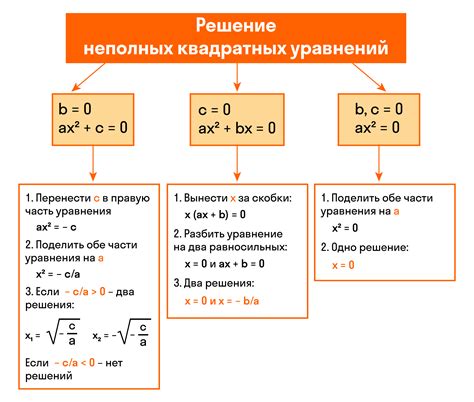
Для наглядности рассмотрим несколько примеров решения квадратного уравнения с помощью Python.

1. Уравнение: 3x^2 - 7x + 2 = 0

   Решение:

   • Дискриминант: D = (-7)^2 - 4 * 3 * 2 = 49 - 24 = 25
   • Корни уравнения: x_1 = (-(-7) + sqrt(25)) / (2 * 3) = (7 + 5) / 6 = 2 и x_2 = (-(-7) - sqrt(25)) / (2 * 3) = (7 - 5) / 6 = 1/3

2. Уравнение: 2x^2 + 5x - 3 = 0

   Решение:

   • Дискриминант: D = 5^2 - 4 * 2 * (-3) = 25 + 24 = 49
   • Корни уравнения: x_1 = (-5 + sqrt(49)) / (2 * 2) = (-5 + 7) / 4 = 1/2 и x_2 = (-5 - sqrt(49)) / (2 * 2) = (-5 - 7) / 4 = -3

3. Уравнение: x^2 - 4x + 4 = 0

   Решение:

   • Дискриминант: D = (-4)^2 - 4 * 1 * 4 = 16 - 16 = 0
   • Корень уравнения: x = -(-4) / (2 * 1) = 4 / 2 = 2

Это лишь некоторые примеры, но вы можете применить алгоритм решения квадратного уравнения в Python для любых других уравнений данного типа.

Реализация формулы дискриминанта

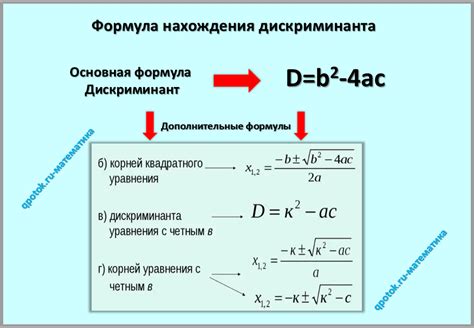
Для реализации формулы дискриминанта в Python, сначала необходимо получить значения коэффициентов квадратного уравнения: a, b и c. Затем используя эти значения, можно вычислить значение дискриминанта по формуле:

Д = b^2 - 4ac

После вычисления дискриминанта, можно проанализировать его значение для определения типа решений:

• Если Д > 0, то уравнение имеет два различных решения.
• Если Д = 0, то уравнение имеет одно решение (корень).
• Если Д

Реализация формулы дискриминанта в Python может выглядеть примерно так:

def solve_quadratic_equation(a, b, c):
discriminant = b**2 - 4*a*c
if discriminant > 0:
# Вычислить и вывести два различных решения
x1 = (-b + discriminant ** 0.5) / (2*a)
x2 = (-b - discriminant ** 0.5) / (2*a)
print("Уравнение имеет два различных решения:", x1, "и", x2)
elif discriminant == 0:
# Вычислить и вывести одно решение
x = -b / (2*a)
print("Уравнение имеет одно решение:", x)
else:
print("Уравнение не имеет решений.")

Пример использования функции solve_quadratic_equation:

solve_quadratic_equation(1, -5, 6)

Таким образом, реализация формулы дискриминанта позволяет эффективно решать квадратные уравнения в Python и получать корректные результаты в соответствии с правилами математики.

Поиск корней квадратного уравнения

D = b² - 4ac

Если дискриминант положительный, то уравнение имеет два различных корня:

x₁ = (-b + √D) / 2a

x₂ = (-b - √D) / 2a

Если дискриминант равен нулю, то уравнение имеет один корень:

x = -b / 2a

Если дискриминант отрицательный, то уравнение не имеет действительных корней.

В Python можно воспользоваться функцией sqrt() из модуля math для вычисления квадратного корня. Пример кода:

a = 1
b = 5
c = 6
D = b**2 - 4*a*c
if D > 0:
x1 = (-b + math.sqrt(D)) / (2*a)
x2 = (-b - math.sqrt(D)) / (2*a)
print("У уравнения два различных корня:", x1, "и", x2)
elif D == 0:
x = -b / (2*a)
print("У уравнения один корень:", x)
else:
print("У уравнения нет действительных корней")

Обработка исключений при решении квадратного уравнения

При решении квадратного уравнения в Python возможны ситуации, когда некоторые значения приводят к ошибкам или неправильным результатам. Для обработки таких ситуаций в языке Python используются механизмы исключений.

Примером возможной ошибки может быть деление на ноль при вычислении дискриминанта или деление на ноль при вычислении корней уравнения. Для обработки ошибок и предотвращения аварийного завершения программы рекомендуется использовать конструкцию try-except вокруг кода, который может вызвать исключение.

try:

      # код, который может вызвать исключение

except ИмяОшибки:

      # код обработки исключения

try:

      дискриминант = б ** 2 - 4 * а * с

      корень_1 = (-б + дискриминант ** 0.5) / (2 * а)

      корень_2 = (-б - дискриминант ** 0.5) / (2 * а)

      print("Корни уравнения:", корень_1, корень_2)

except ValueError:

      print("Для заданных коэффициентов корни уравнения не существуют")

Используя механизмы исключений, можно предусмотреть обработку различных исключительных ситуаций и уведомить пользователя о возникших ошибках. Это позволяет сделать программу более надежной и удобной в использовании.

Возможные сложности при решении квадратного уравнения

Решение квадратного уравнения может вызвать некоторые сложности из-за его особенностей. Вот некоторые из них:

1. Квадратное уравнение может иметь разные типы корней: два различных вещественных корня, два одинаковых вещественных корня или два комплексных корня.
2. Если дискриминант уравнения равен нулю, то уравнение имеет только один корень.
3. При вычислении дискриминанта может возникнуть проблема с точностью при работе с числами с плавающей точкой.
4. Если уравнение имеет комплексные корни, то нахождение их может потребовать дополнительных вычислений и использования модуля комплексных чисел.
5. Возможны ошибки ввода данных пользователем, такие как неправильное написание уравнения или использование некорректных символов.

При решении квадратного уравнения важно учитывать эти сложности и предусмотреть соответствующие проверки и обработку возможных ошибок. Например, можно добавить проверку на дискриминант перед вычислением корней уравнения или предложить пользователю повторно ввести данные в случае ошибки. Это поможет избежать неправильных результатов и обеспечить корректную работу программы.