Квадратные уравнения – один из базовых и наиболее изучаемых математических объектов. Они позволяют нам найти неизвестное значение (или значения) переменной, которое удовлетворяет данному уравнению.
Одним из способов решения квадратных уравнений является использование дискриминанта. Дискриминант – это число, которое мы получаем из коэффициентов квадратного уравнения и которое позволяет определить, сколько корней имеет это уравнение.
В этом подробном гиде мы рассмотрим, как использовать дискриминант для решения квадратных уравнений. Мы покажем, как вычислить дискриминант и как на основе его значения получить корни уравнения. Кроме того, мы также рассмотрим различные случаи, которые могут возникнуть при решении квадратных уравнений через дискриминант.
Определение квадратных уравнений

Коэффициенты a, b и c могут быть любыми реальными числами, но чтобы уравнение было квадратным, коэффициент a должен быть неравным нулю. Если a = 0, то уравнение уже не будет квадратным, а будет линейным.
Решение квадратного уравнения означает нахождение всех значений переменной x, которые удовлетворяют данному уравнению. Квадратное уравнение может иметь ноль, один или два корня. Корни уравнения - это значения переменной x, при которых уравнение равно нулю.
- Если D > 0, то уравнение имеет два различных корня.
- Если D = 0, то уравнение имеет один корень.
- Если D , то уравнение не имеет действительных корней.
Для решения квадратного уравнения можно использовать формулу корней, которая имеет вид:
x = (-b ± √(D)) / (2a)
Эта формула позволяет найти значения переменной x с помощью дискриминанта.
Расчет дискриминанта

Для квадратного уравнения вида ax^2 + bx + c = 0 дискриминант вычисляется по формуле:
D = b^2 - 4ac
где:
- a, b и c - коэффициенты квадратного уравнения
- D - значение дискриминанта
После расчета дискриминанта можно определить, сколько корней имеет квадратное уравнение:
- Если D > 0, то уравнение имеет два разных вещественных корня
- Если D = 0, то уравнение имеет один вещественный корень
- Если D < 0, то уравнение не имеет вещественных корней
Расчет дискриминанта - первый и важнейший шаг в решении квадратного уравнения через дискриминант. От его значения зависит дальнейший алгоритм решения уравнения.
Решение уравнений через дискриминант
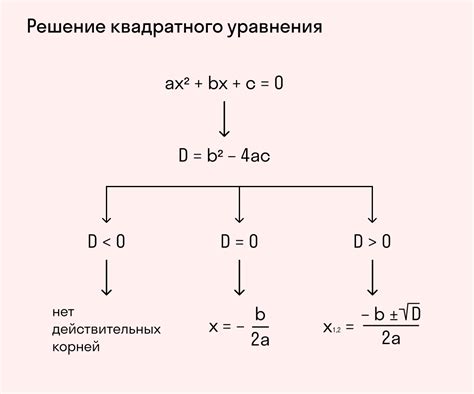
Для решения уравнения ax^2 + bx + c = 0, где a, b и c - коэффициенты, необходимо вычислить дискриминант по формуле D = b^2 - 4ac. Дискриминант показывает характер уравнения:
- Если D > 0, то уравнение имеет два различных корня: x1 и x2.
- Если D = 0, то уравнение имеет один корень: x.
- Если D
Если дискриминант больше или равен нулю (D ≥ 0), то применяются следующие формулы для нахождения корней:
- x1 = (-b + √D) / (2a)
- x2 = (-b - √D) / (2a)
Если дискриминант меньше нуля (D
- x1 = (-b + i√(|D|)) / (2a)
- x2 = (-b - i√(|D|)) / (2a)
Поэтому, решение уравнения через дискриминант является универсальным методом, позволяющим определить корни квадратного уравнения.
Примеры решения уравнений

Для того чтобы проиллюстрировать процесс решения квадратных уравнений через дискриминант, рассмотрим несколько примеров.
Пример 1:
Рассмотрим уравнение 2x2 - 5x + 2 = 0.
Сначала найдем дискриминант по формуле: D = b2 - 4ac.
В данном случае, a = 2, b = -5, и c = 2. Подставим значения в формулу:
D = (-5)2 - 4 * 2 * 2 = 25 - 16 = 9.
Так как дискриминант положительный, уравнение имеет два различных решения.
Затем найдем корни уравнения, используя формулу: x = (-b ± √D) / (2a).
Подставим значения и вычислим:
| Решение уравнения | Значение x |
|---|---|
| Первый корень | x1 = (-(-5) + √9) / (2 * 2) = (5 + 3) / 4 = 8 / 4 = 2 |
| Второй корень | x2 = (-(-5) - √9) / (2 * 2) = (5 - 3) / 4 = 2 / 4 = 0.5 |
Таким образом, уравнение 2x2 - 5x + 2 = 0 имеет два корня: x = 2 и x = 0.5.
Пример 2:
Рассмотрим уравнение x2 + 6x + 9 = 0.
Найдем дискриминант:
D = 62 - 4 * 1 * 9 = 36 - 36 = 0.
Так как дискриминант равен нулю, уравнение имеет одно решение.
Вычислим решение уравнения:
| Решение уравнения | Значение x |
|---|---|
| Единственное решение | x = (-6) / (2 * 1) = -3 |
Таким образом, уравнение x2 + 6x + 9 = 0 имеет одно решение: x = -3.
Примеры решения уравнений через дискриминант помогают наглядно понять процесс и получить практические навыки в решении квадратных уравнений.