Геометрия - наука о фигурах, и одной из самых известных фигур является квадрат. Квадрат является регулярным четырехугольником, у которого все стороны равны между собой и все углы прямые. Такой простой и изящный геометрический объект часто используется в строительстве, дизайне и искусстве.
Процесс построения квадрата может быть представлен в нескольких шагах. Первым шагом является рисование прямой линии, которая будет служить основой для будущего квадрата. Если вы рисуете на бумаге, используйте линейку для получения прямой линии. Если вы рисуете на компьютере или планшете, используйте инструменты рисования для создания прямой линии.
Вторым шагом является построение второй перпендикулярной прямой, которая будет также равна первой. Для этого используйте угломер, чтобы получить прямой угол между первой линией и новой. Убедитесь, что величина угла равна 90 градусам. Затем, используя линейку, нарисуйте прямую линию, которая будет пересекать первую линию так, чтобы образовался прямоугольник.
Третьим шагом является проведение линий, соединяющих концы прямых и образующих стороны квадрата. Используйте линейку или угломер для получения правильных углов и равной величины сторон. Удостоверьтесь, что все стороны квадрата равны между собой и все углы прямые.
В результате выполнения этих шагов вы получите идеальный квадрат. Изучение геометрии и умение рисовать простые фигуры полезно не только для уроков математики, но и для развития логического мышления и творческого воображения. Так что не бойтесь экспериментировать и нарисовать свой собственный квадрат!
Геометрия и ее элементы

Один из основных элементов геометрии - это точка. Точка является базовым понятием и не имеет ни размеров, ни формы. Точки могут служить началом для построения других геометрических объектов.
Линия - это набор бесконечно маленьких точек, расположенных в определенном порядке. Линия является одномерным объектом, который имеет длину, но не ширину или высоту.
Окружность - это фигура, состоящая из всех точек, расположенных на одинаковом расстоянии от центра. Окружность имеет радиус (расстояние от центра до любой точки на окружности) и диаметр (удвоенный радиус).
| Название | Описание |
|---|---|
| Квадрат | Это четырехугольник, все стороны которого равны друг другу, а углы - прямые. |
| Прямоугольник | Это четырехугольник, у которого противоположные стороны равны и углы - прямые. |
| Треугольник | Это трехугольный полигон, который состоит из трех сторон и трех углов. |
| Параллелограмм | Это четырехугольник, у которого противоположные стороны параллельны друг другу. |
| Трапеция | Это четырехугольник, у которого две стороны параллельны, а две другие - нет. |
| Ромб | Это четырехугольник, у которого все стороны равны друг другу. |
Это только некоторые элементы геометрии. В реальности их существует гораздо больше, и они играют важную роль в решении геометрических задач и применении геометрии в различных областях науки и техники.
Свойства квадрата
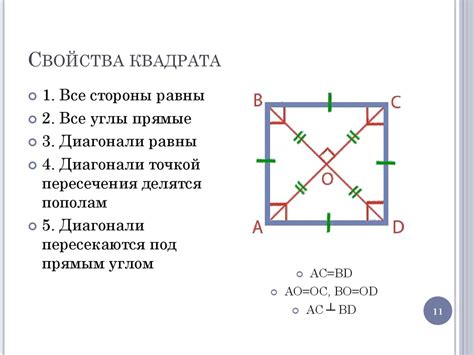
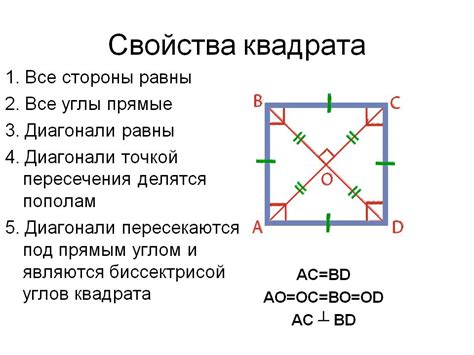
Основные свойства квадрата:
| 1. | Все стороны квадрата равны между собой. |
| 2. | Углы квадрата равны 90 градусам. |
| 3. | Диагонали квадрата равны между собой и делят его на два равных прямоугольных треугольника. |
| 4. | Периметр квадрата равен сумме длин всех его сторон. |
| 5. | Площадь квадрата равна квадрату длины его стороны. |
Свойства квадрата делают его удобным для использования в различных задачах, например, для создания равных поверхностей или для строительства.
Понятие периметра и площади квадрата
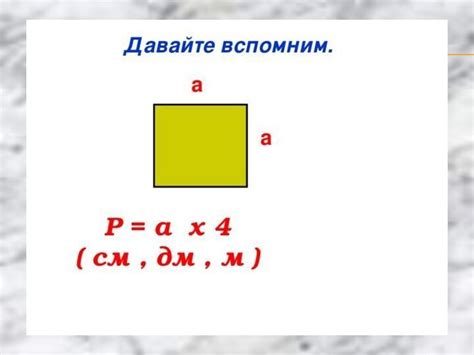
Периметр квадрата - это сумма длин всех его сторон. Так как все стороны квадрата равны, то периметр можно вычислить по формуле: П = 4 * а, где "а" - длина одной стороны квадрата.
Квадрат также имеет понятие площади - это количество площади, занимаемой квадратом на плоскости. Площадь квадрата можно вычислить по формуле: S = а * а, где "а" - длина одной стороны квадрата.
К примеру, если длина стороны квадрата равна 5 см, то его периметр будет равен 20 см (4 * 5) и площадь будет равна 25 квадратным сантиметрам (5 * 5).
Понимание периметра и площади квадрата позволяет лучше понять геометрические свойства этой фигуры и правильно применять соответствующие формулы при решении задач и конструировании.
| Свойства | Квадрат |
|---|---|
| Периметр | П = 4 * а |
| Площадь | S = а * а |
Практическое рисование квадрата
- Возьмите лист бумаги и ручку.
- Начните с рисования вертикальной линии. Она будет служить одной из сторон квадрата. Выберите длину этой линии в соответствии с желаемым размером квадрата.
- От вершины вертикальной линии, нарисуйте еще одну линию под углом 90 градусов. Это будет вторая сторона квадрата, параллельная первой.
- Теперь соедините конец второй линии с ее началом, нарисовав горизонтальную линию такой же длины как вертикальная.
- Наконец, закончите рисование квадрата, соединив конец горизонтальной линии с началом вертикальной с помощью последней вертикальной линии.
Теперь у вас есть квадрат, который можно использовать в учебных целях или в качестве элемента дизайна. Ура!