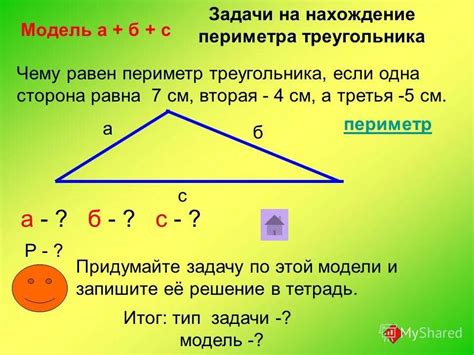
Периметр треугольника – это сумма всех его сторон. Задача по нахождению периметра треугольника во втором классе является одной из основных в математике. Важно знать формулу и уметь применять ее на практике, чтобы решать подобные задачи и вести успешное обучение.
Формула для нахождения периметра треугольника имеет несколько вариантов в зависимости от известной информации о треугольнике:
1. Если известны длины всех трех сторон треугольника, то периметр можно найти, сложив все три стороны: периметр = сторона1 + сторона2 + сторона3.
2. Если известна длина одной из сторон треугольника и его высота, то можно воспользоваться формулой: периметр = сторона + боковая сторона1 + боковая сторона2, где сторона - известная сторона треугольника, а боковая сторона1 и боковая сторона2 - это длины отрезков, проведенных из вершины треугольника и перпендикулярных известной стороне.
Рассмотрим пример:
У нас есть треугольник со сторонами длиной 5 см, 7 см и 9 см. Найдем его периметр.
Используем формулу: периметр = сторона1 + сторона2 + сторона3.
Подставляем значения: периметр = 5 см + 7 см + 9 см = 21 см.
Таким образом, периметр треугольника равен 21 см.
Методы нахождения периметра треугольника
Если известны длины всех сторон треугольника, то периметр можно найти, просто сложив эти длины.
Если известны координаты вершин треугольника в декартовой системе координат, то периметр можно найти, используя формулу расстояния между двумя точками. Нужно найти расстояния между всеми парами вершин и сложить их. Формула расстояния между двумя точками выглядит так:
AB = √((x2-x1)²+(y2-y1)²)
где A(x1, y1) и B(x2, y2) – координаты двух точек.
Также существует формула Герона, которая позволяет найти периметр треугольника, если известны длины его сторон. Формула выглядит так:
P = a + b + c
где P – периметр треугольника, а, b, c – длины его сторон.
Важно помнить, что для корректного решения задачи необходимо правильно определить единицы измерения и записать ответ с указанием единицы измерения периметра (например, см или м).
Формула периметра для треугольника

Следуя формуле периметра, периметр треугольника вычисляется по следующей формуле:
P = a + b + c
Где P - периметр треугольника, a, b и c - длины его сторон.
Например, если известны длины сторон треугольника и они равны 5, 3 и 4, то используя формулу периметра мы можем найти его значение:
P = 5 + 3 + 4 = 12
Таким образом, периметр этого треугольника равен 12.
Используя данную формулу, можно легко вычислить периметр любого треугольника, зная длины его сторон.
Примеры расчета периметра треугольника

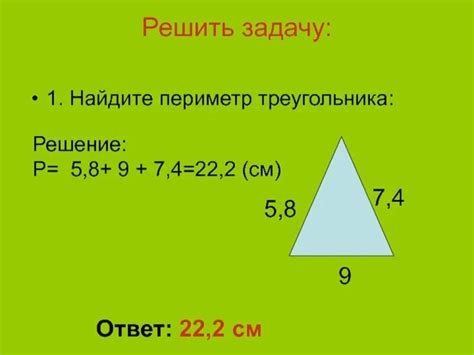
Периметр треугольника можно найти суммируя длины всех его сторон. Вот несколько примеров расчета периметра треугольника:
Треугольник ABC с заданными сторонами:
- Сторона AB: 5 см
- Сторона BC: 7 см
- Сторона CA: 3 см
Для нахождения периметра, нужно сложить длины всех сторон: 5 см + 7 см + 3 см = 15 см
Ответ: Периметр треугольника ABC равен 15 см
Треугольник XYZ с заданными сторонами:
- Сторона XY: 8 см
- Сторона YZ: 4 см
- Сторона ZX: 6 см
Для нахождения периметра, нужно сложить длины всех сторон: 8 см + 4 см + 6 см = 18 см
Ответ: Периметр треугольника XYZ равен 18 см
Треугольник PQR с заданными сторонами:
- Сторона PQ: 10 см
- Сторона QR: 12 см
- Сторона RP: 16 см
Для нахождения периметра, нужно сложить длины всех сторон: 10 см + 12 см + 16 см = 38 см
Ответ: Периметр треугольника PQR равен 38 см
Таким образом, для расчета периметра треугольника необходимо сложить длины всех его сторон. Зная длины сторон, можно легко найти периметр треугольника.
Развитие умений по нахождению периметра треугольника на уроках математики
На уроках математики во втором классе активно развиваются навыки по нахождению периметра треугольника. Это важная тема, которая помогает развить у детей логическое мышление, усвоить математические понятия и применять их на практике.
Процесс нахождения периметра треугольника начинается с определения его сторон. Ученикам объясняют, что периметр треугольника - это сумма длин всех его сторон. Для того чтобы найти периметр, дети должны измерить длину каждой стороны с помощью линейки и сложить результаты.
Преподаватели используют различные методы и подходы, чтобы сделать изучение периметра треугольника интересным и понятным. Они могут проводить игры, упражнения на нахождение периметра треугольника на рисунках или использовать различные материалы для измерений. Например, учащимся могут предлагать измерить длины сторон треугольника с помощью шнурка или бумажной ленты.
Также учителя стараются дать детям практические примеры, чтобы показать, где и как используется нахождение периметра треугольника в реальной жизни. Например, ученикам объясняют, что периметр треугольника может понадобиться для построения ограды вокруг сада или для определения длины проволоки перед покупкой.
Развитие умений по нахождению периметра треугольника помогает детям не только понять основные понятия математики, но и применять их в повседневной жизни. Это важная предметная область, которая способствует формированию у детей уверенности в своих математических способностях и развитию аналитического мышления.
Практическое применение нахождения периметра треугольника в реальной жизни

Знание периметра треугольника может быть полезным в строительстве и архитектуре. Например, если вы строите забор или ограждение, вы должны знать, какой будет периметр, чтобы правильно рассчитать необходимое количество материала. Точный расчёт периметра треугольника поможет вам выбрать и приобрести нужное количество кабелей или проводов для электроустановок, поблизости от строительства.
Также, знание периметра треугольника может быть полезным в географии и картографии. Например, исследователи и географы используют периметр треугольника для определения расстояний между точками на карте или поверхности Земли. Это актуально в путешествии, а также для обновления и создания новых карт, глобусов и навигационных систем.
Периметр треугольника также имеет практическое применение в финансовой сфере. Например, при расчете стоимости ограждения для футбольного поля, участка земли или при оценке расходов на строительство здания или транспортного сооружения, периметр треугольника поможет определить стоимость необходимого материала и оценить бюджет проекта.
Однако, население не всегда обращается к периметру треугольника напрямую в повседневной жизни. Вместо этого, мы часто используем готовые формулы и инструменты для вычисления периметра, такие как калькуляторы и компьютерные программы. Несмотря на это, знание того, как найти периметр треугольника, остается важным навыком, который может быть применен во многих сферах нашей жизни.