Ордината – это значение, отображающее вертикальную координату точки на графике. В процессе анализа графиков функций, построенных в системе координат, бывает необходимо точно определить ординату для конкретной точки. В этой статье мы рассмотрим несколько методов и рекомендаций, которые помогут вам найти ординату точки графика.
Первый метод – использование уравнений функции. Если у вас есть уравнение функции, то вы можете подставить значение абсциссы точки в это уравнение и вычислить соответствующую ей ординату. Например, для функции y = 2x + 3, чтобы найти ординату точки с абсциссой x = 4, нужно подставить значение 4 вместо x: y = 2 * 4 + 3 = 11.
Второй метод – использование координатной сетки графика. Если у вас есть изображение графика с координатной сеткой, вы можете визуально определить ординату точки. Для этого найдите нужную абсциссу точки на оси x и проведите линию от этой точки до графика функции. Затем с помощью вертикальной линейки или зрительно определите значение ординаты на оси y. Например, если абсцисса точки равна 3, а ордината равна 5, то координаты этой точки будут (3, 5).
Изучение графика функции

Первым шагом при изучении графика функции является построение графика на координатной плоскости. Для этого необходимо задать значения аргумента функции и вычислить соответствующие значения функции. Полученные значения можно отобразить на графике, соединив их линиями или точками.
Далее, необходимо определить значения функции в различных точках графика. Для этого можно использовать графический метод, который заключается в измерении значений функции на графике с помощью линейки или других инструментов. Также можно использовать аналитический метод, который заключается в вычислении значений функции с использованием математических формул и уравнений.
Определение точек максимума и минимума функции на графике также является важной задачей при изучении графика функции. Для этого необходимо найти точки, в которых функция достигает наибольшего или наименьшего значения. Для поиска таких точек можно использовать графический метод, визуально находя экстремумы функции на графике. Также можно использовать аналитический метод, вычисляя значения производной функции и равномерность её изменения.
Дополнительно, при изучении графика функции можно учитывать особенности, такие как асимптоты и периодические закономерности. Асимптоты являются прямыми или кривыми линиями, к которым график функции стремится, но никогда не пересекает. Они могут быть горизонтальными, вертикальными или наклонными. Периодические закономерности могут иметь место, если функция повторяется с определенной периодичностью.
Изучение графика функции является важным инструментом для понимания её поведения и свойств. При изучении графика функции необходимо учитывать его основные характеристики, определять значения функции в различных точках, находить точки максимума и минимума, а также учитывать особенности графика, такие как асимптоты и периодические закономерности.
Определение основных характеристик графика

Основные характеристики графика позволяют определить его форму, характер зависимости переменных и другие важные детали. Вот несколько основных характеристик графика:
1. Зависимая и независимая переменные: Зависимая переменная обычно откладывается на оси ординат (вертикальной оси), а независимая переменная – на оси абсцисс (горизонтальной оси). Значения зависимой переменной определяются значениями независимой переменной.
2. Масштаб: Масштаб графика определяет, насколько велика часть графика на рисунке. Масштаб может быть одинаковым для обеих осей или различным.
3. Тип графика: Графики могут быть разных типов, включая линейные, параболические, экспоненциальные и другие. Тип графика может быть определён по его форме и характеру изменения переменных.
4. Угол наклона: Угол наклона графика показывает, насколько быстро меняется зависимая переменная при изменении независимой переменной. Угол наклона может быть положительным или отрицательным, а также может быть нулевым (горизонтальный график) или бесконечным (вертикальный график).
5. Пересечение с осями: Точки пересечения графика с осями абсцисс и ординат позволяют определить значения переменных в этих точках. Они могут иметь особое значение и помогать в анализе данных.
6. Экстремумы и точки перегиба: Экстремумы графика – это точки, в которых достигаются максимальное или минимальное значение зависимой переменной. Точки перегиба – это точки, в которых меняется направление изгиба графика.
Тщательное анализирование этих основных характеристик графика позволяет получить более глубокое понимание зависимости между переменными и выделить важные моменты для дальнейшего исследования данных.
Использование математических методов

Например, если у нас есть уравнение прямой вида y = kx + b, где k – коэффициент наклона, а b – свободный член, то чтобы найти ординату точки графика с известным значением абсциссы, необходимо подставить значение абсциссы вместо x и вычислить значение y.
Если же у нас есть уравнение функции более сложного вида, например, кубической функции, то для определения ординаты точки нужно найти значение функции при заданном значении абсциссы. Для этого абсциссу подставляют в уравнение функции и производят необходимые вычисления.
Использование математических методов позволяет точно определить ординату точки графика и дает возможность провести дополнительные вычисления для более сложных функций.
Метод половинного деления

Идея метода состоит в следующем. Пусть у нас есть функция f(x), заданная на интервале [a, b], и нам нужно найти такое значение x, при котором f(x) равно заданной ординате y. Сначала выбираются начальные значения a и b таким образом, чтобы f(a) и f(b) были разных знаков. Затем находится середина интервала [a, b], то есть значение c = (a + b) / 2. Если f(c) равно y (с точностью до заданной погрешности), то x = c - искомый корень найден. Если f(c) не равно y, то выбирается новый интервал [a, b] таким образом, чтобы f(a) и f(b) были разных знаков, и процесс повторяется.
Метод половинного деления является итерационным, поэтому для достижения требуемой точности может потребоваться несколько итераций. Однако он гарантирует сходимость и может быть применен для нахождения ординаты точки на графике с высокой точностью.
Применение алгоритма Ньютона
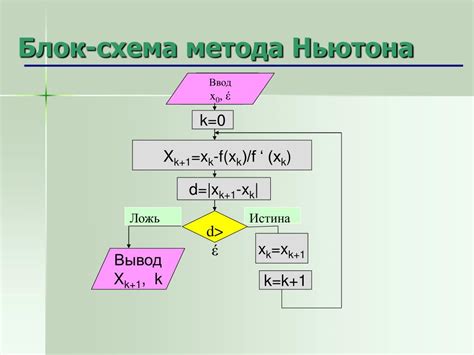
Алгоритм Ньютона основан на идее последовательных приближений к искомому значению функции. Сначала выбирается начальное приближение, затем по формуле осуществляются последующие итерации до достижения необходимой точности.
Процесс алгоритма Ньютона можно описать следующими шагами:
- Выбрать начальное приближение для ординаты точки на графике.
- Вычислить значение функции и ее производную в данной точке.
- Используя формулу Ньютона-Рафсона, получить новое приближение для ординаты.
- Повторять шаги 2 и 3 до достижения нужной точности.
Алгоритм Ньютона обладает быстрой сходимостью к искомому значению функции, однако может оказаться неустойчивым, если начальное приближение выбрано неверно или функция имеет особенности в окрестности искомой точки. Поэтому важно выбирать начальное приближение с учетом особенностей функции и контекста задачи.
Применение алгоритма Ньютона может быть широко использовано для нахождения ординаты точки на графике в различных областях, таких как математика, физика, экономика и многих других.
Основные принципы алгоритма

Для нахождения ординаты точки на графике существует несколько основных принципов алгоритма. Рассмотрим их подробнее:
1. Построение графика функции.
Первым шагом необходимо построить график функции, на котором находится искомая точка. Для этого можно использовать различные математические программы или графические калькуляторы. График позволяет наглядно представить зависимость переменных и определить положение точки.
2. Определение координат точки.
Зная положение точки на графике, можно определить ее координаты. При этом используются оси координат, на которых точка имеет свои значения абсциссы и ординаты. Абсцисса определяет горизонтальное положение точки, а ордината - вертикальное положение.
3. Использование математических методов.
Для точных вычислений ординаты необходимо применять различные математические методы, в зависимости от уравнения функции, на основе которого построен график. Например, для линейной функции ордината может быть найдена путем подстановки абсциссы в уравнение функции.
4. Проверка полученных результатов.
Важным шагом является проверка полученных результатов. Для этого можно использовать различные методы, такие как графическое сравнение с графиком функции или проверка с использованием других математических инструментов. Это позволяет удостовериться в правильности найденной ординаты и исключить возможные ошибки.
В целом, основными принципами алгоритма нахождения ординаты точки на графике являются строительство графика, определение координат точки, использование математических методов и проверка полученных результатов. Соблюдение этих принципов позволяет найти ординату точки графика с высокой точностью.
Использование программных средств
Для нахождения ординаты точки графика существуют различные программные средства, которые значительно упрощают эту задачу. В настоящее время существует огромное количество специализированных программ и онлайн-сервисов, которые позволяют визуально представить график и легко определить координаты интересующей точки. Они позволяют не только найти ординату точки, но и проводить различные другие операции с графиками.
Для использования программных средств обычно достаточно ввести значения абсциссы и найти соответствующую ординату на экране. Некоторые программы позволяют вводить уравнение графика или импортировать данные из файла, что позволяет работать с более сложными функциями или наборами данных.
Программные средства также позволяют визуализировать графики в различных форматах, сохранять их в файлы или публиковать в Интернете. Это очень удобно, если вам необходимо предоставить графики для работы или поделиться ими с другими людьми.
Однако стоит отметить, что для использования программных средств требуется определенный набор навыков и знаний. Вам может понадобиться обучение или инструкция для работы с конкретной программой. Тем не менее, современные программы обычно имеют интуитивно понятный интерфейс, что делает процесс поиска ординаты точки графика достаточно простым и удобным.
Использование программных средств предоставляет широкие возможности для нахождения ординаты точки графика и работы с графиками в целом. Это удобный и эффективный способ получить результаты с минимальными затратами усилий и времени.