Одно из самых важных понятий в геометрии и математике - это понятие треугольника. Небольшой, но столь универсальный геометрический объект, треугольник способен решать различные задачи нахождения расстояний или углов.

Синус и косинус - это тригонометрические функции, которые связаны с углами и отношениями сторон треугольников. Используя эти функции, мы можем определить длину сторон треугольника, включая катеты.

Например, если нам известен угол треугольника и длина одного из катетов, мы можем использовать функцию синуса или косинуса, чтобы найти длину другого катета. Эта информация может быть очень полезной при решении различных физических задач или в конструировании различных устройств.

Основные принципы нахождения катетов с помощью синуса и косинуса

Для нахождения катетов с помощью синуса и косинуса необходимо знать значение угла и длину одного из катетов. Допустим, у нас есть прямоугольный треугольник ABC, где угол B равен искомому углу, сторона AB является искомым катетом, а сторона AC - известным катетом.

Для нахождения искомого катета с помощью синуса, можно воспользоваться следующей формулой:

AB = AC * sin(B)

Для нахождения искомого катета с помощью косинуса, можно воспользоваться следующей формулой:

AB = AC * cos(B)

Значение синуса и косинуса угла B можно найти, используя тригонометрическую таблицу или калькулятор. После нахождения значений синуса и косинуса, можно просто умножить их на известный катет и получить значение искомого катета.

Например, если у нас есть прямоугольный треугольник со сторонами AC = 5 и углом B = 30 градусов, то мы можем найти значение катета AB с помощью синуса:

AB = 5 * sin(30) = 5 * 0.5 = 2.5

Таким образом, значение катета AB равно 2.5. Аналогично можно использовать формулу с косинусом, если известно значение косинуса угла B.

Нахождение катетов с помощью синуса и косинуса позволяет решать различные задачи, связанные с треугольниками, и является важным элементом в изучении геометрии и тригонометрии.

Запасаемся формулами для нахождения катетов по тригонометрическим функциям

При решении задач на нахождение катетов прямоугольного треугольника с помощью тригонометрических функций, мы использовать синус и косинус. Зная значение этих функций и значение гипотенузы, можем найти длину катета.

Для нахождения длины катета, если известны значение угла и гипотенузы, используем формулу косинуса:

катет_по_косинусу = гипотенуза * cos(угол)

Если нам известно значение угла и длины катета, для нахождения гипотенузы используется формула косинуса:

гипотенуза = катет / cos(угол)

Для нахождения длины катета, если известны значение угла и гипотенузы, используем формулу синуса:

катет_по_синусу = гипотенуза * sin(угол)

Если нам известно значение угла и длины катета, для нахождения гипотенузы используется формула синуса:

гипотенуза = катет / sin(угол)

Освоив эти простые формулы, вы сможете легко решать задачи на нахождение катетов и гипотенузы в прямоугольных треугольниках, используя тригонометрические функции.

Как определить значение угла при помощи синуса и косинуса

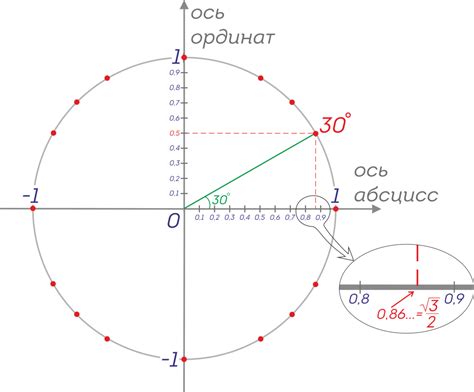
Синус угла в прямоугольном треугольнике определяется как отношение противолежащего катета к гипотенузе. Из формулы синуса следует, что синус угла можно выразить как отношение величины противолежащего катета к длине гипотенузы:

sin(A) = противолежащий катет / гипотенуза

Аналогично, косинус угла в прямоугольном треугольнике определяется как отношение прилежащего катета к гипотенузе. Из формулы косинуса следует, что косинус угла можно выразить как отношение величины прилежащего катета к длине гипотенузы:

cos(A) = прилежащий катет / гипотенуза

Найдя значения синуса и косинуса угла, мы можем использовать обратные функции для определения значения самого угла. Например, для нахождения значения угла по известному значению синуса можно использовать арксинус (или инверсный синус) функцию:

A = arcsin(противолежащий катет / гипотенуза)

Точно так же, для нахождения значения угла по известному значению косинуса можно использовать арккосинус (или инверсный косинус) функцию:

A = arccos(прилежащий катет / гипотенуза)

Эти формулы и функции позволяют определить значение угла в прямоугольном треугольнике при известных значениях синуса и косинуса. Они являются важными инструментами для решения задач и проведения измерений в различных областях науки и инженерии.

Ищем катет с использованием синуса

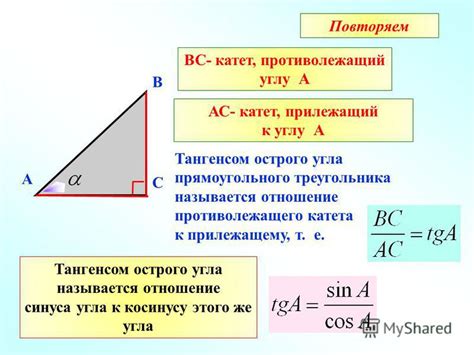
Формула для нахождения длины катета с использованием синуса выглядит следующим образом:

катет = гипотенуза * синус (угла)

Где:

• катет - длина противолежащего катета
• гипотенуза - длина гипотенузы
• синус (угла) - значение синуса угла, заданное в радианах или градусах

Для примера, допустим у нас есть прямоугольный треугольник с углом в 30 градусов и гипотенузой длиной 10 единиц. Чтобы найти длину противолежащего катета, мы можем использовать формулу:

катет = 10 * синус (30)

Подставляя значения в формулу, получим:

катет = 10 * 0.5 = 5

Таким образом, длина противолежащего катета равна 5 единицам.

Находим катет с использованием косинуса

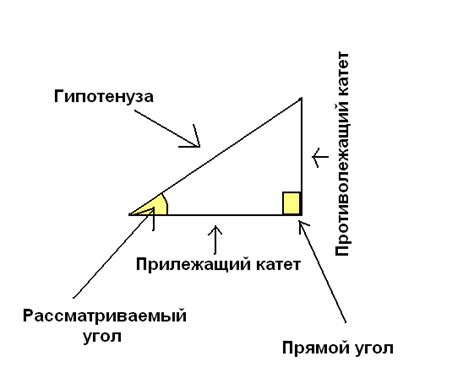
Косинус угла в прямоугольном треугольнике равен отношению длины прилежащего катета к гипотенузе.

Чтобы найти длину катета, используем формулу:

Катет = Гипотенуза * Косинус угла

1. Определите длину гипотенузы и угол между гипотенузой и искомым катетом.

2. Найдите значение косинуса угла, используя таблицы или калькулятор.

3. Подставьте значения гипотенузы и косинуса угла в формулу и рассчитайте длину катета.

4. Полученное значение будет являться длиной искомого катета.

Применяем тригонометрию для вычисления катетов в практических задачах

Допустим, у нас есть треугольник, углы которого известны, а длина одного из катетов нужно найти. Возьмем, к примеру, треугольник ABC, где угол A равен 30 градусов, угол B равен 90 градусов, а угол C равен 60 градусов. Допустим, нам нужно найти длину катета AB.

При помощи синуса угла B мы можем записать равенство:

sin(B) = AB / AC

Так как мы знаем, что угол B равен 90 градусов, то sin(90) = 1. Значит:

1 = AB / AC

Значение AC - это гипотенуза треугольника, и она нам известна. Например, допустим, AC = 10.

Теперь мы можем выразить AB:

AB = 1 * AC

AB = 1 * 10

AB = 10

Таким образом, мы получили, что длина катета AB равна 10.

Аналогичным образом можно вычислить длину катета в других треугольниках, зная значения углов и длину гипотенузы.

Такие вычисления могут быть полезны в контексте строительства, прямых линий, различных измерений и т.д.