Гипербола является одной из форм второго порядка в математике и имеет свои особенности в построении. Построение гиперболы по таблице позволяет визуализировать ее форму и основные параметры. Если вы хотите понять, как построить таблицу гиперболы на глаз, вам потребуется знание основных шагов и инструкций.

Первый шаг в построении таблицы гиперболы – определение центра координатной системы, в которой будет происходить построение. Центр можно выбрать на удобное для вас место на плоскости. После этого нужно определить оси координат и их направление. Обычно оси называются OX и OY. OX – ось абсцисс, OY – ось ординат.

Далее вам потребуется уравнение гиперболы, которое имеет вид:

x²/a² - y²/b² = 1

Параметры a и b определяют форму гиперболы и ее конфигурацию. Для построения таблицы вам потребуется ряд значений для x и y. Выберите диапазон значений для x и по каждому значению вычислите соответствующее значение y. Запишите полученные значения в таблицу.

Определите уравнение гиперболы

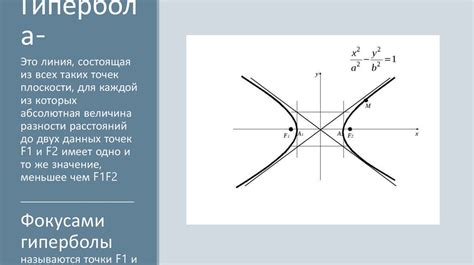
Чтобы построить таблицу гиперболы на глаз, важно сначала определить ее уравнение. Уравнение гиперболы имеет следующий вид:

• Если гипербола расположена вертикально и центр находится в точке (h, k), то уравнение имеет форму (x - h)^2 / a^2 - (y - k)^2 / b^2 = 1. Здесь a - полуось по оси x, b - полуось по оси y.
• Если гипербола расположена горизонтально и центр находится в точке (h, k), то уравнение имеет форму (x - h)^2 / b^2 - (y - k)^2 / a^2 = 1. Здесь a - полуось по оси y, b - полуось по оси x.

Важно знать значения полуосей a и b, а также координаты центра гиперболы (h, k), чтобы правильно построить таблицу гиперболы. Если у вас есть эти данные, можно перейти к следующему шагу и начать построение таблицы гиперболы на глаз.

Постройте оси симметрии гиперболы

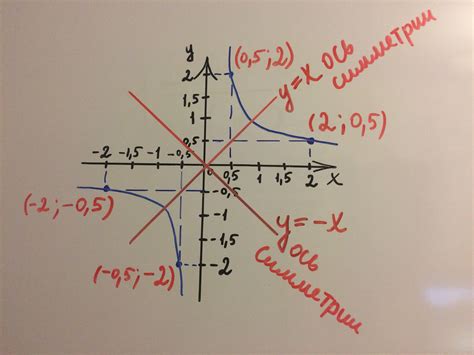
1. Найдите центр гиперболы. Для этого определите вершины гиперболы и наклон осей относительно центра.
2. Проведите главную ось гиперболы, проходящую через центр и вершины гиперболы.
3. Получите вторую ось симметрии, проведя прямую через центр, перпендикулярную главной оси гиперболы.

Построение осей симметрии поможет определить форму и расположение гиперболы на плоскости.

Найдите точку пересечения осей симметрии

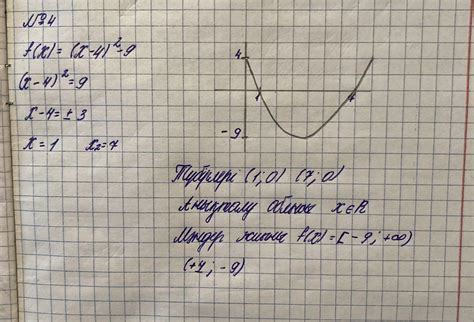
Для нахождения точки пересечения горизонтальной оси следует приравнять уравнение гиперболы к нулю и решить это уравнение относительно переменной x. Полученное значение x будет являться координатой точки пересечения. Аналогично, для нахождения точки пересечения вертикальной оси, уравнение гиперболы следует приравнять к нулю и решить его относительно переменной y.

Таким образом, нахождение точек пересечения осей симметрии позволяет определить начальные точки построения таблицы гиперболы и обеспечивает симметричность графика относительно этих осей.

Постройте характерные точки гиперболы

Для построения гиперболы на глаз, важно определить характеристические точки, которые помогут нам понять ее форму и свойства.

1. Центр гиперболы: чтобы найти центр гиперболы, нужно найти середину между фокусами, которые указывают на оси гиперболы. Центр будет обозначаться точкой (h, k).

2. Фокусы: фокусы гиперболы находятся на оси симметрии и обозначаются точками F1 и F2. Расстояние от центра гиперболы до фокусов обозначается как c.

3. Директрисы: директрисы гиперболы - это две параллельные прямые, находящиеся на одинаковом расстоянии от центра гиперболы на противоположных сторонах. Они обозначаются как D1 и D2.

4. Вершины: вершины гиперболы - это точки на горизонтальных и вертикальных осях, которые соединяют точку центра с точками пересечения гиперболы с этими осями.

5. Асимптоты: асимптоты гиперболы - это две прямые, которые выступают в качестве границы гиперболы в бесконечности. Они проходят через фокусы и пересекаются в точке, которая находится на оси симметрии гиперболы.

Используя данные характерные точки, можно построить гиперболу на глаз, имея представление о ее форме и свойствах.