Косинус угла - это одна из основных тригонометрических функций, которая широко используется в математике и физике. Ознакомление с понятием косинуса и его вычисление может помочь в решении различных задач, связанных с анализом углов и векторов.
Если вы только начинаете изучать тригонометрию или хотите разобраться в том, как найти косинус угла, то в этой статье мы расскажем вам пять полезных советов.
1. Используйте формулу косинусов
Одним из основных способов вычисления косинуса угла является использование формулы косинусов. Эта формула позволяет вычислить косинус угла, если известны две стороны треугольника и угол между ними. Формула выглядит следующим образом: cos(A) = (b² + c² - a²) / (2bc), где A - угол, a, b и c - стороны треугольника.
Пример: Пусть у вас есть треугольник ABC, где стороны a = 5, b = 4 и c = 3, а угол A - искомый угол. Тогда по формуле косинусов можно вычислить косинус A, подставив значения в формулу: cos(A) = (4² + 3² - 5²) / (2 * 4 * 3) = (16 + 9 - 25) / 24 = 0.75.
2. Используйте таблицы значений
Если вы хотите вычислить косинус угла, необходимо знать его значение. Воспользуйтесь таблицей косинусов с известными значениями для различных углов от 0° до 90°. По таблице можно определить значение косинуса для конкретного угла.
Пример: Для угла 30° таблица показывает, что cos(30°) = 0.866.
3. Используйте калькулятор или специализированные программы
В наше время есть множество калькуляторов и специализированных программ, которые могут вычислить косинус угла за вас. Эти инструменты позволяют быстро и точно найти значение косинуса, освобождая вас от необходимости самостоятельно выполнять вычисления.
4. Используйте геометрические свойства
В геометрии существуют некоторые свойства, которые могут помочь вычислить косинус угла без использования формулы. Например, в прямоугольном треугольнике косинус угла равен отношению прилежащего катета к гипотенузе.
Пример: Пусть у вас есть прямоугольный треугольник ABC, где угол A = 30°, катет AB = 3 и гипотенуза AC = 5. Тогда косинус угла A равен отношению длины катета AB к длине гипотенузы AC: cos(A) = AB / AC = 3 / 5 = 0.6.
5. Разберитесь в геометрических фигурах
Для вычисления косинуса угла полезно иметь знания о геометрических фигурах, таких как окружность, треугольник и шестиугольник. Понимание основных свойств этих фигур может помочь найти значения косинусов углов.
Определение косинуса угла
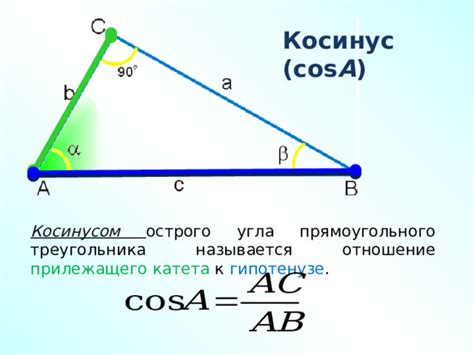
cos(A) = adjacent/hypotenuse
Значение косинуса угла всегда находится в диапазоне от -1 до 1. Если угол составляет 90 градусов, то косинус равен 0, так как противолежащий катет равен нулю.
Косинус угла также может быть определен с помощью тригонометрического круга. Для этого, по отметке на окружности, можно определить значения косинуса угла для углов 0, 30, 45, 60 и 90 градусов.
Знание косинуса угла может быть полезным при решении различных задач математики, физики, инженерии и других научных дисциплин. Он используется для вычисления расстояний, при решении проблем оптики и многих других задач.
Угол и его смысл в математике
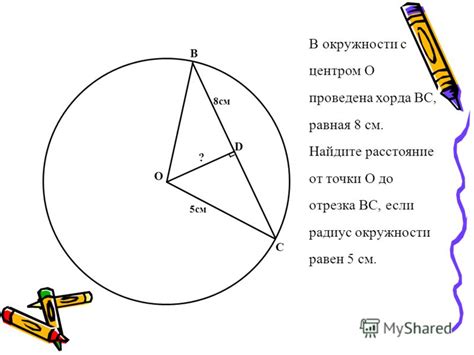
Углы в геометрии являются одним из фундаментальных понятий. Они широко применяются для описания и измерения форм и отношений между пространственными объектами. Углы играют важную роль в решении задач, связанных с геометрией и тригонометрией.
Смысл угла в математике заключается в определении отношений между различными направлениями или объектами. Углы используются для изучения и описания изменений, поворотов и сдвигов в пространстве. Они помогают анализировать и предсказывать различные явления и процессы, которые происходят в природе, технике и других областях науки.
Типы углов:
- Острый угол: угол, меньший 90 градусов.
- Прямой угол: угол, равный 90 градусам.
- Тупой угол: угол, больший 90 градусов.
- Полный угол: угол, равный 360 градусам или 2π радианам.
Знание и понимание углов помогает в решении множества задач и проблем, связанных с анализом, измерением и моделированием различных явлений и объектов.
Формула косинуса
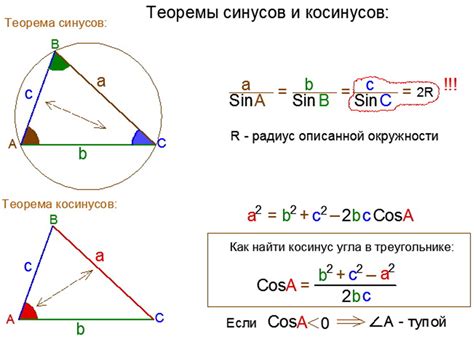
Формула косинуса имеет вид:
cos(α) = a / c
где α - это значение угла, а a и c - длины сторон треугольника.
Для использования формулы косинуса нужно знать значения длин сторон треугольника и значение угла. Затем подставить эти значения в формулу и вычислить косинус угла. Он может принимать значения от -1 до 1.
Нахождение косинуса угла может быть полезно в различных областях математики и науки, таких как геометрия, физика, инженерия и другие.
Практические советы по нахождению косинуса
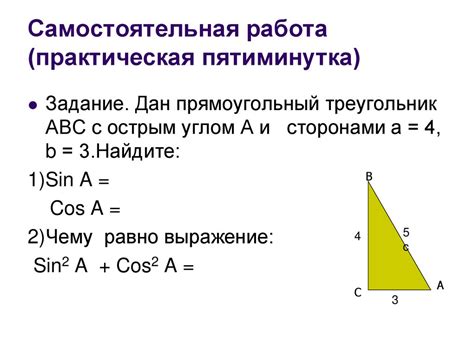
Вот пять полезных советов, которые помогут вам в нахождении косинуса угла:
| 1. | Используйте тригонометрические таблицы: |
| 2. | Используйте калькулятор: |
| 3. | Применяйте формулу cos(α) = adj/hyp: |
| 4. | Используйте набор основных значений косинуса: |
| 5. | Используйте тригонометрические свойства: |
Следуя этим практическим советам, вы сможете легко и быстро вычислять косинус угла и успешно применять его в различных задачах.
Косинусы известных углов
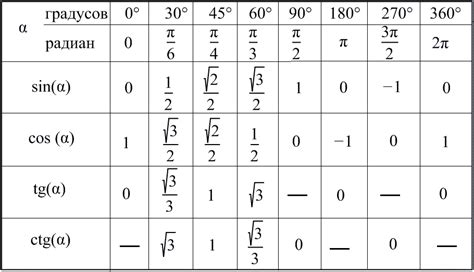
Ниже приведена таблица с известными значениеми косинусов для некоторых углов:
| Угол, градусы | Косинус |
|---|---|
| 0 | 1 |
| 30 | √3/2 |
| 45 | √2/2 |
| 60 | 1/2 |
| 90 | 0 |
Эти значения косинусов являются базовыми и широко используются при решении задач по геометрии, физике и других областях науки и техники.