Вычисление кубического корня в уравнении может быть сложной задачей для многих людей. Однако, с некоторыми советами, примерами и методами, процесс может быть значительно упрощен. В данной статье мы рассмотрим несколько способов, которые помогут вам в вычислении кубического корня, а также предоставим примеры, чтобы вы лучше поняли, как это работает.
Прежде всего, важно понимать, что кубический корень является обратной операцией возведения в куб. То есть, если у вас есть число, возведенное в куб, чтобы найти его кубический корень, необходимо найти число, которое было возвещено в куб. Например, если у вас есть число 8, его куб равен 512. Чтобы найти кубический корень из 512, вам нужно найти число, которое при возведении в куб будет равно 512.
Один из наиболее распространенных методов для вычисления кубического корня - это использование табличных значений. Можно составить таблицу с кубами чисел от 0 до 9, и затем найти ближайшее значение куба заданного числа. Затем, с использованием интерполяции, можно рассчитать приблизительное значение кубического корня. Например, если заданное число равно 27, можно увидеть, что ближайшее значение куба равно 8. Затем, с учетом этого значения и таблицы, можно получить приблизительное значение для корня, которое равно примерно 3.
Что такое кубический корень в уравнении

В уравнении кубический корень может использоваться для решения уравнений вида x^3 = a, где a - известное число. Кубический корень от a обозначается как ∛a или a^(1/3).
Вычисление кубического корня может быть сложной задачей. Однако существуют специальные методы и приближенные значения, которые помогают упростить этот процесс. Такие методы включают использование таблиц кубов и разложение на множители.
Кубический корень в уравнении может иметь как одно, так и три различных решения. Все три решения называются корнями кубического уравнения.
Важно отметить, что кубический корень может иметь как положительное, так и отрицательное значение. В случае кубического уравнения положительное значение кубического корня обычно используется как основное решение.
Определение и основные понятия
Кубический корень может быть положительным или отрицательным. Например, кубический корень из 8 равен 2, так как 2 в кубе равно 8. Однако, кубический корень из -8 равен -2, так как -2 в кубе также равно -8.
Кубический корень в уравнении может быть выражен через математический символ √, и записывается следующим образом: √(x) или x1/3. Например, кубический корень из 27 можно записать как √(27) или 271/3, что равно 3.
Для упрощения вычисления кубического корня в уравнении можно использовать различные методы, такие как взятие кубического корня из целых чисел, десятичных чисел, или использование специальных формул для преобразования сложных выражений.
- Для вычисления кубического корня из целых чисел можно использовать простой метод, заключающийся в повторном делении числа на различные числа и проверке, является ли результат кубическим корнем.
- Для вычисления кубического корня из десятичных чисел можно использовать приближенные методы, такие как метод Ньютона, метод бисекции или метод пристрелки.
- Для упрощения сложных выражений с кубическими корнями можно использовать специальные формулы, например, формулы Виета или формулы кубических корней.
Упрощение вычисления кубического корня в уравнении может значительно сэкономить время и усилия при решении математических задач и уравнений, а также позволить получить более точный результат.
Как упростить вычисление кубического корня: советы и методы
Вычисление кубического корня может быть сложной задачей, но с помощью определенных советов и методов вы сможете упростить этот процесс.
1. Используйте кубическую функцию
Одним из самых простых способов вычислить кубический корень является использование встроенной кубической функции в математическом программном обеспечении или калькуляторе. Просто введите число и функцию вернет вам кубический корень.
2. Разложите число на множители
Если вам нужно найти кубический корень числа, которое может быть разложено на множители, вы можете воспользоваться этим свойством. Разложите число на множители и извлеките кубический корень из каждого множителя. Затем умножьте найденные корни.
3. Используйте приближенные методы
Для поиска приближенного значения кубического корня можно использовать методы приближенного вычисления, например метод Ньютона. Эти методы позволяют найти приближенное значение кубического корня с заданной точностью.
4. Будьте внимательны к знаку
Когда вы вычисляете кубический корень из отрицательного числа, помните о комплексных числах. Результатом будет комплексный корень, который будет иметь мнимую и действительную часть. Обратите внимание на знаки в выражении, чтобы правильно интерпретировать результат.
В итоге, вычисление кубического корня может быть сложной задачей, но с помощью этих советов и методов вы сможете упростить этот процесс и получить более точные результаты.
Метод нахождения кубического корня с помощью десятичного логарифма
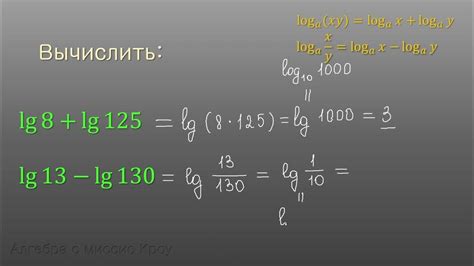
Вычисление кубического корня от числа может быть тривиальной задачей с использованием десятичного логарифма. Десятичный логарифм представляет собой логарифм по основанию 10 и позволяет нам упростить сложные вычисления.
Для нахождения кубического корня мы можем использовать следующий метод.
- Первым шагом является вычисление десятичного логарифма исходного числа, используя стандартные математические функции или таблицы логарифмов.
- Затем, мы делим полученное значение десятичного логарифма на 3, так как мы ищем кубический корень.
- Полученное значение делим на десятичный логарифм основания 10, чтобы получить окончательный результат.
Применение данного метода позволяет нам значительно упростить вычисления и найти кубический корень приближенно. Однако стоит отметить, что это приближенное решение и может иметь небольшую погрешность.
Вот пример применения этого метода:
- Дано число 125.
- Вычисляем десятичный логарифм числа 125, получаем значение 2.096.
- Делим полученное значение на 3, получаем значение примерно равное 0.699.
- Делим полученное значение на десятичный логарифм основания 10 (приближенно равен 0.434), получаем результат примерно равный 1.609.
Таким образом, кубический корень от числа 125 приближенно равен 1.609.
Использование десятичного логарифма для нахождения кубического корня позволяет нам упростить вычисления и получить представление о приближенном значении. Этот метод особенно полезен, когда нам нужно быстро оценить грубое приближение кубического корня без использования сложных математических вычислений.
Советы для упрощения вычисления кубического корня

Вычисление кубического корня может быть сложным процессом, но с некоторыми советами можно упростить эту задачу.
1. Используйте калькулятор или программу расчета, чтобы получить точный результат. Кубические корни могут быть десятичными дробями, поэтому может быть более точно использовать инструмент для вычисления.
2. Выучите несколько кубических корней для наиболее распространенных чисел. Например, кубический корень из 8 равен 2, а кубический корень из 27 равен 3. Зная эти основные значения, вы сможете приближенно оценивать кубические корни других чисел.
3. Используйте свойства алгебры, чтобы упростить вычисления. Например, если у вас есть уравнение вида (a + b)^3 = c, вы можете разложить его с помощью формулы (a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3. Затем вы можете использовать уже известные кубические корни, чтобы упростить полученное выражение.
4. Пользуйтесь табличными данными, если они доступны. Видя кубические корни других чисел, вы можете найти закономерности и использовать их в своих вычислениях.
| Число | Кубический корень |
|---|---|
| 1 | 1 |
| 2 | 1.26 |
| 3 | 1.44 |
| 4 | 1.69 |
| 5 | 1.71 |
Не бойтесь экспериментировать и использовать разные подходы к вычислению кубического корня. С практикой и опытом вы станете более уверенными и опытными в этой области математики.
Примеры вычисления кубического корня в уравнениях

Вычисление кубического корня в уравнениях может быть сложной задачей, особенно при больших числах или в научных расчетах. Однако, с помощью некоторых методов и приемов, можно упростить этот процесс.
Вот несколько примеров, демонстрирующих использование различных методов вычисления кубического корня в уравнениях:
Пример 1:
Дано уравнение: x^3 = 64
Для вычисления кубического корня из 64 можно использовать метод простой декомпозиции:
64 = 4 * 4 * 4
Таким образом, кубический корень из 64 равен 4.
Ответ: x = 4
Пример 2:
Дано уравнение: x^3 + 8 = 0
Для вычисления кубического корня из -8 можно использовать метод комплексных чисел:
Кубический корень из -8 равен -2, так как (-2)^3 = -8.
Ответ: x = -2
Пример 3:
Дано уравнение: x^3 - 27 = 0
Для вычисления кубического корня из 27 можно использовать метод формулы разности кубов:
x^3 - 27 = (x - 3)(x^2 + 3x + 9)
Таким образом, получим два возможных значения:
x - 3 = 0, x = 3
x^2 + 3x + 9 = 0 - нет решений
Ответ: x = 3
Это лишь некоторые из возможных методов для вычисления кубического корня в уравнениях. В зависимости от конкретной задачи и доступных инструментов, можно выбрать подходящий метод или сочетание методов.
Важно помнить, что корни уравнений могут быть как рациональными, так и иррациональными числами, а также комплексными числами. Поэтому, необходимо учитывать все возможные варианты при решении уравнений.
Пример вычисления кубического корня при помощи аппроксимации
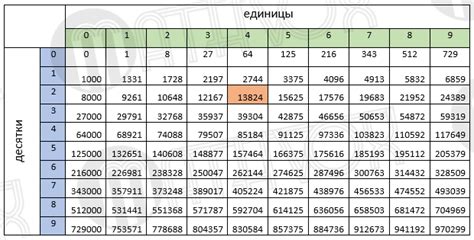
Метод аппроксимации основан на том, что мы можем приближенно вычислить кубический корень путем выбора начального приближения и последовательного уточнения его значения.
Допустим, мы хотим вычислить кубический корень числа 27. Воспользуемся методом аппроксимации:
- Шаг 1: Выберем начальное приближение для кубического корня. Допустим, мы выберем 3 как начальное приближение.
- Шаг 2: Вычислим новое приближение для кубического корня по формуле: (2 * приближение + число / приближение^2) / 3. В нашем случае: (2 * 3 + 27 / 3^2) / 3 = (6 + 27 / 9) / 3 = (6 + 3) / 3 = 9 / 3 = 3.
- Шаг 3: Повторяем шаг 2 до тех пор, пока новое приближение не перестанет изменяться с заданной точностью.
В результате применения метода аппроксимации, мы получаем значение кубического корня числа 27 равным 3.
Метод аппроксимации является простым способом приближенного вычисления кубического корня. Однако, он не всегда дает точный результат и может потребовать большого количества итераций для достижения нужной точности. При более сложных вычислениях, рекомендуется использовать более точные алгоритмы.
Пример использования графического метода для нахождения кубического корня
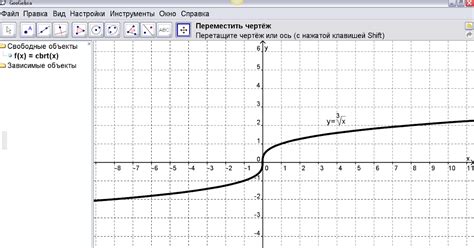
Для того чтобы использовать графический метод, необходимо взять уравнение вида x^3 = a, где a - исходное значение, для которого требуется найти кубический корень.
Шаги по применению графического метода:
- Выбрать произвольное начальное значение x.
- Вычислить значение функции y = x^3 - a.
- Если значение y отрицательное, увеличить x на некоторую величину и перейти к шагу 2. Если значение y положительное, уменьшить x на некоторую величину и перейти к шагу 2.
- Повторять шаги 2-3 до тех пор, пока значение y не станет достаточно близким к нулю, что будет указывать на близкое значение кубического корня a.
Например, для нахождения кубического корня числа 8 с использованием графического метода, можно выбрать начальное значение x = 2 и перейти к шагу 2.
Вычисляя значение функции для выбранного значения x, получим:
- y = 2^3 - 8 = 8 - 8 = 0
Так как значение y равно нулю, это указывает на то, что x = 2 является корнем исходного уравнения x^3 = 8.
Однако, если значение y не равно нулю, необходимо изменять значение x и повторять шаги 2-3 до тех пор, пока не будет получено значение, близкое к нулю.
Графический метод позволяет приближенно находить кубический корень числа без использования сложных математических вычислений. Однако, следует помнить, что результаты могут быть некоторым образом неточными, так как графический метод основан на аппроксимации значений.
Пример применения метода Ньютона для поиска кубического корня

Для иллюстрации применения метода Ньютона для нахождения кубического корня рассмотрим следующий пример. Пусть нам необходимо вычислить кубический корень из числа 27. Математически, это означает, что нам нужно найти такой x, что x^3 = 27.
Начнем с выбора начального приближения для x, например, x0 = 3. Затем мы можем применить формулу итерации метода Ньютона:
| n | xn | f(xn) | f'(xn) | xn+1 |
|---|---|---|---|---|
| 0 | 3 | 18 | 9 | 2.66667 |
| 1 | 2.66667 | 3.96296 | 7.11111 | 2.44298 |
| 2 | 2.44298 | 1.32193 | 5.16991 | 2.25102 |
| 3 | 2.25102 | 0.15789 | 4.50204 | 2.08013 |
| 4 | 2.08013 | 0.00728 | 4.16026 | 2.01285 |
| 5 | 2.01285 | 5.7796e-05 | 4.00256 | 2.00082 |
Процесс итерации продолжается до тех пор, пока не будет достигнута заданная точность. В данном примере мы получили приближенное значение кубического корня из числа 27 равное 2.00082.
Таким образом, метод Ньютона является мощным инструментом для вычисления кубического корня и позволяет получить приближенное значение с высокой точностью. Он широко применяется в науке и технике для решения различных задач, связанных с кубическими корнями.