Создание функций является одним из основных аспектов программирования. В этой статье мы рассмотрим, как создать функцию, которая будет возводить число в квадрат.

Для начала, давайте определим, что такое функция. Функция - это некоторый блок кода, который принимает аргументы и возвращает результат. В нашем случае, мы хотим создать функцию, которая будет принимать число, возводить его в квадрат и возвращать результат.

Для этого мы можем использовать язык программирования Python. В нём есть встроенная функция pow, которая позволяет возводить число в степень. Мы можем использовать эту функцию для решения нашей задачи.

Вот как будет выглядеть код создания функции:

В этом коде мы определяем функцию с именем square, которая принимает один аргумент x. Внутри функции мы используем функцию pow, передавая ей аргумент x и степень 2. Результат возведения в квадрат мы возвращаем с помощью ключевого слова return.

Чтобы протестировать нашу функцию, мы можем вызвать её с помощью следующего кода:

Теперь мы знаем, как создать функцию, которая возводит число в квадрат. Эта функция может быть полезной во многих задачах программирования.

Шаг 1: Определение функции

Вот как выглядит определение функции:

def square(x):

    y = x * x

Когда вы вызываете эту функцию с каким-либо значением аргумента x, она вернет значение y - квадрата этого значения.

Основные характеристики функции

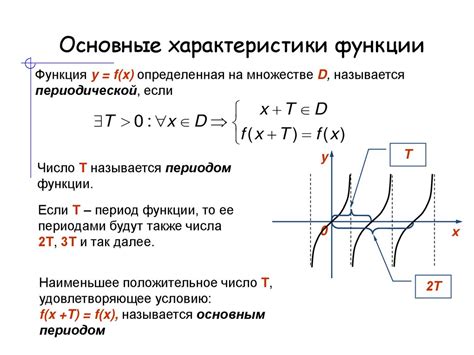
• Аргументы: функция y=x^2 зависит от значения аргумента x, который может быть любым числом. Аргументы функции позволяют определить, какие значения могут быть подставлены в функцию.
• Значения: функция y=x^2 возвращает значение y, которое является результатом вычисления квадрата аргумента x. Значения функции могут быть числами или другими объектами в зависимости от контекста задачи.
• Область определения: функция y=x^2 определена для всех действительных чисел. Область определения функции указывает, какие значения аргумента могут быть использованы в функции.
• Область значений: функция y=x^2 имеет область значений, которая также составляет множество всех действительных чисел. Область значений описывает, какие значения могут быть получены в результате вычисления функции.
• График: функция y=x^2 может быть представлена в виде графика на координатной плоскости, где x представлен по горизонтальной оси, а y по вертикальной оси. График функции y=x^2 имеет форму параболы, открывающейся вверх.
• Симметрия: функция y=x^2 обладает осевой симметрией относительно оси y, что означает, что значения функции для симметричных относительно оси y аргументов равны.

Понимание этих основных характеристик функции поможет в создании функции y=x^2 пошагово и более глубоком ее изучении.

Шаг 2: Создание основного кода

Для создания функции y=x^2 пошагово воспользуемся языком программирования JavaScript. Следующий код будет реализовывать данную функцию:

function calculateSquare(x) {
return Math.pow(x, 2);
}
// Пример использования функции
var input = 5;
var result = calculateSquare(input);

Инструкция по написанию кода функции

1. Откройте новый файл в редакторе кода или интегрированной среде разработки (IDE).
2. Начните с объявления функции с помощью ключевого слова def и имени функции, например, def square(x):.
3. В теле функции, используйте оператор return для возврата значения квадрата числа x с помощью оператора возведения в степень: return x ** 2.
4. Сохраните файл с расширением .py, например, square_function.py.
5. Запустите файл, чтобы протестировать функцию. Вызовите функцию и передайте ей аргумент, например, result = square(5).
6. Выведите результат, используя функцию print(): print(result).

Это основы написания кода функции y = x^2 пошагово. После освоения этой инструкции вы сможете использовать исходный код функции, чтобы вычислять квадраты чисел и решать математические задачи в своих программах.

Шаг 3: Тестирование и отладка

После создания функции y=x^2, следующим шагом будет проведение тестирования и отладки, чтобы убедиться в правильности работы функции. Этот шаг позволит нам исправить возможные ошибки и улучшить функцию по необходимости.

Первым шагом тестирования будет проверка функции на нескольких известных значениях аргумента x. Мы можем взять несколько произвольных значений x и вычислить y по формуле y=x^2 вручную. Затем сравним полученные значения y с результатами, возвращаемыми функцией. Если значения совпадают, это говорит о правильности работы функции.

После внесения изменений и исправления ошибок необходимо провести повторное тестирование функции на известных значениях x, чтобы убедиться в его правильности после изменений.

Тестирование и отладка являются важными этапами в создании функций и помогают обнаружить и исправить возможные ошибки. Важно быть внимательным и методичным при проведении тестирования и анализе работы функции для достижения желаемого результата.