Логические выражения являются неотъемлемой частью программирования и различных алгоритмических решений. Они позволяют нам принимать решения на основе заданных условий и управлять потоком выполнения программы. Важным аспектом работы с логическими выражениями является умение строить их схемы.

Схема для логического выражения представляет собой графическое представление всех составляющих его элементов, таких как операторы сравнения, логические операторы и операнды. С помощью схемы мы можем визуализировать логику выражения и легко определить его результат в зависимости от заданных условий.

Построение схемы для логического выражения начинается с выделения основных операторов сравнения и логических операторов в выражении. Затем мы соединяем их стрелками, указывая направление потока выполнения. Операнды, как правило, представляются в виде значений или переменных.

Давайте посмотрим на пример. Предположим, у нас есть логическое выражение (a > b) && (c < d). Для построения схемы мы выделяем операторы сравнения: a > b и c < d. Затем соединяем их с помощью логического оператора &&. Получившаяся схема позволяет нам легко понять, что результат выражения будет истинным только в том случае, если оба оператора сравнения истинны.

Основы построения схемы логического выражения

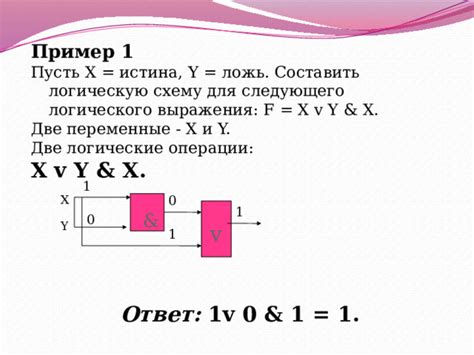
Построение схемы логического выражения позволяет визуализировать его структуру и логику, что упрощает его анализ и понимание. Схема позволяет представить выражение в виде блоков, связанных логическими операторами, и отразить различные ветвления и условия.

При построении схемы логического выражения следует руководствоваться некоторыми основными принципами:

1. Разбить выражение на логические блоки с помощью скобок. Это поможет определить порядок выполнения операций и учесть приоритет операторов.
2. Использовать логические операторы (И, ИЛИ, НЕ) для связи блоков и определения их взаимосвязи.
3. Отобразить вложенность блоков с помощью внутренних блоков и связей между ними.
4. Продумать и обозначить переменные и константы, которые используются в выражении.
5. Добавить комментарии, если необходимо разъяснить основные элементы схемы.

Пример схемы логического выражения может выглядеть следующим образом:

+---------+
|   И     |
+---------+
/           \
+------+             +------+
| ИЛИ  |             | НЕ   |
+------+             +------+
/                        |
+------+------+        +-------+-------+
|Переменная 1 |        |Константа False|
+-------------+        +---------------+

В данном примере используются операторы И (AND), ИЛИ (OR) и НЕ (NOT), а также переменная и константа. Схема наглядно показывает порядок выполнения операций и связи между элементами выражения.

Построение схемы логического выражения помогает не только при его анализе, но и при разработке программного кода, особенно в случаях, когда выражение содержит множество логических операций и условий. Схема позволяет увидеть структуру выражения в целом и выявить потенциальные ошибки или недочеты.

Примеры построения схемы для простых логических выражений

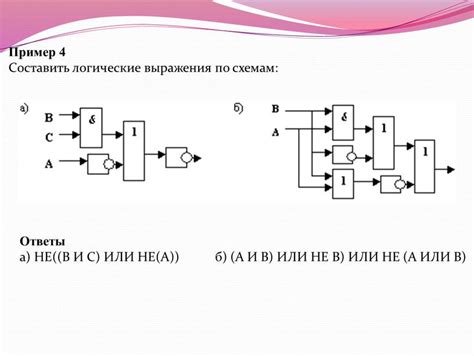
• Пример 1: Логическое И

Выражение: A И B

Схема:



• Пример 2: Логическое ИЛИ

Выражение: A ИЛИ B

Схема:



• Пример 3: Логическое НЕ

Выражение: НЕ A

Схема:



• Пример 4: Комбинированное выражение

Выражение: (A И B) ИЛИ НЕ C

Схема:

В каждом из этих примеров видно, как логические операции влияют на структуру схемы. Таким образом, построение схемы помогает визуально представить и анализировать сложные логические выражения.

Сложные логические выражения: примеры и подходы к построению схемы

Логические выражения, состоящие из нескольких условий, называются сложными. Они позволяют строить более гибкие и точные логические схемы, которые учитывают различные ситуации и условия.

Вот несколько примеров сложных логических выражений:

1. Выражение A И B, где A и B - простые логические выражения. Это выражение будет истинным только в том случае, если оба выражения A и B истинны.
2. Выражение A ИЛИ B, где A и B - простые логические выражения. Это выражение будет истинным, если хотя бы одно из выражений A и B истинно.
3. Выражение НЕ А, где А - простое логическое выражение. Это выражение будет истинным только в том случае, если выражение А ложно.

При построении схемы для сложных логических выражений можно использовать различные подходы:

1. Использование блок-схем. Блок-схемы позволяют представить каждое условие и результат его выполнения в виде блока со стрелками, которые показывают переход к следующему блоку в зависимости от результата.
2. Использование таблиц истинности. Таблицы истинности позволяют представить все возможные варианты значений для каждого условия и определить результат логического выражения в каждом случае.

Выбор подхода зависит от сложности выражения и предпочтений разработчика. Важно выбрать наиболее удобный и понятный способ для построения схемы.

Например, для выражения A И B можно построить блок-схему, где на каждом блоке указано условие и результат его выполнения. Для выражения A ИЛИ B можно использовать таблицу истинности, чтобы определить результат для каждого возможного значения A и B. А для выражения НЕ A также можно использовать блок-схему, где указано условие и результат его выполнения.

Сложные логические выражения позволяют учесть большое количество условий и сделать программу или систему более гибкой и функциональной. При их применении важно выбрать правильный подход к построению схемы, чтобы легко и понятно представить логику работы выражения.

Особые случаи при построении схемы логического выражения

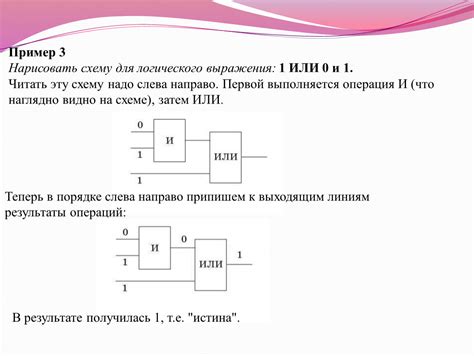
При построении схемы логического выражения могут возникнуть некоторые особые случаи, которые требуют особого внимания. В этом разделе рассмотрим несколько таких случаев.

1. Вложенные выражения. Если в логическом выражении содержатся вложенные выражения, то их следует приоритезировать, чтобы избежать недоразумений. Для этого можно использовать скобки или другие способы группировки. Например, выражение A AND (B OR C) будет означать, что сначала выполняется выражение внутри скобок, а затем результат AND-операции применяется к A.

2. Условные операторы. В случае, когда логическое выражение содержит условные операторы, такие как IF-THEN или CASE, необходимо обратить внимание на возможные варианты и соответствующие результаты. При построении схемы следует учесть все возможные ветвления и их логические связи.

3. Неоднозначность. Иногда логическое выражение может быть неоднозначным и иметь несколько возможных интерпретаций. В таких случаях следует уточнить правила для определения приоритета выполнения операций. Например, выражение A AND B OR C может быть интерпретировано как (A AND B) OR C или A AND (B OR C), в зависимости от заданных правил.

Учитывая эти особые случаи, можно построить более точную и надежную схему для логического выражения. Это поможет избежать ошибок и позволит лучше понять логику выражения.