Создание таблицы функции - это важный навык, который необходимо освоить уже в 7 классе. Таблица функции позволяет упорядочить и представить все значения функции в виде удобной и структурированной таблицы. В этой статье мы рассмотрим пошаговую инструкцию по созданию таблицы функции, чтобы вы могли без проблем выполнять такие задания на уроках математики.
На первом шаге необходимо записать заданную функцию, например, y = 2x + 3. Здесь y обозначает значение функции, а x - независимую переменную. Затем мы выбираем значения для переменной x и подставляем их в функцию, чтобы найти соответствующие значения y. Например, выберем значения x = 0, 1, 2, 3 и подставим их в функцию.
Для первого значения x = 0, подставляем его в функцию: y = 2(0) + 3 = 3. Для второго значения x = 1, подставляем его в функцию: y = 2(1) + 3 = 5. Для третьего значения x = 2, подставляем его в функцию: y = 2(2) + 3 = 7. Аналогично, для четвертого значения x = 3, получаем y = 2(3) + 3 = 9.
Теперь мы можем создать таблицу функции, в которой первый столбец будет содержать значения переменной x, а второй столбец - значения функции y. В нашем случае таблица будет выглядеть следующим образом:
| x | y |
|---|---|
| 0 | 3 |
| 1 | 5 |
| 2 | 7 |
| 3 | 9 |
Теперь вы можете легко создать таблицу функции по заданной математической функции. Помните, что таблица функции помогает увидеть зависимость между значениями переменной x и функции y и может быть очень полезна при анализе графиков функций и решении задач на работу с функциями.
Что такое таблица функции?

В таблице функции значения аргумента обычно представлены в первом столбце, а соответствующие им значения функции – во втором столбце. Значения функции отображаются на пересечении строк и столбцов, где соответствующий аргумент и значение функции пересекаются. Это позволяет увидеть, какие значения функции принимаются при разных значениях аргумента.
Таблица функции может быть использована для нахождения закономерностей, поиска максимальных и минимальных значений, а также решения уравнений и неравенств, связанных с функцией. Однако важно помнить, что таблица функции является лишь одним из инструментов анализа функций и может быть дополнена другими методами, такими как построение графика.
Создание таблицы функции может быть полезным упражнением в математике для понимания взаимосвязи между аргументами и значениями функции. Научиться строить и анализировать таблицы функций поможет ученикам развивать навыки критического мышления и логического рассуждения.
Первый шаг - определение функции

Для определения функции следует использовать следующую структуру:
f(x) = ...
Здесь f(x) - обозначение функции, а ... - правило, по которому определяются значения функции для различных значений аргумента.
Например, чтобы задать функцию "f(x) = 2x + 1", можно записать:
f(x) = 2x + 1
Таким образом, первым шагом при создании таблицы функции является определение самой функции с помощью правила, которое задает соответствие между значениями аргумента и значением функции.
Второй шаг - составление таблицы значений функции

Для этого выберите несколько значений аргумента и подставьте их в функцию. Например, если функция задана в виде y = f(x), то выберите несколько значений для переменной x и подставьте их в функцию, чтобы найти соответствующие значения для y.
Давайте рассмотрим пример. Предположим, что у нас есть функция y = 2x + 3. Мы выберем несколько значений для переменной x и найдем соответствующие значения для переменной y.
- Пусть x = 0. Подставим это значение в функцию: y = 2 * 0 + 3 = 3. Таким образом, когда x = 0, y = 3.
- Пусть x = 1. Подставим это значение в функцию: y = 2 * 1 + 3 = 5. Таким образом, когда x = 1, y = 5.
- Пусть x = 2. Подставим это значение в функцию: y = 2 * 2 + 3 = 7. Таким образом, когда x = 2, y = 7.
Таким образом, мы получили следующую таблицу значений для функции y = 2x + 3:
| x | y |
|---|---|
| 0 | 3 |
| 1 | 5 |
| 2 | 7 |
Теперь у вас есть таблица значений для функции y = 2x + 3. Повторите этот процесс для каждой выбранной переменной x и составьте полную таблицу значений для заданной функции.
Третий шаг - построение координатной плоскости

После того как мы определили значения аргумента и нашли соответствующие им значения функции, мы можем перейти к построению координатной плоскости. Координатная плоскость поможет нам наглядно представить зависимость между значениями аргумента и значениями функции.
Для построения координатной плоскости нам понадобится лист бумаги или клетчатый блокнот, ручка или карандаш и линейка.
1. На бумаге или блокноте проведите две перпендикулярные линии, которые будут служить основами координатной плоскости. Одну линию проведите горизонтально, а другую - вертикально.
2. Подписывайте оси координат. Вертикальную ось назовите осью ординат или осью значений функции. Горизонтальную ось назовите осью абсцисс или осью аргумента.
3. На оси абсцисс отложите промежуток, который соответствует диапазону значений аргумента. Если в таблице функции аргумент принимает значения от 1 до 5, то промежуток на оси абсцисс будет соответствовать этому диапазону.
4. Разделите промежуток на оси абсцисс на равные интервалы. Наиболее удобно делить этот промежуток на столько же равных частей, сколько значений аргумента в таблице функции. Например, если значений аргумента 5, то разделите промежуток на 5 равных интервалов.
5. На оси ординат отложите промежуток, который соответствует диапазону значений функции. Если в таблице функции значения функции варьируются от -3 до 3, то промежуток на оси ординат будет соответствовать этому диапазону.
6. Разделите промежуток на оси ординат на равные интервалы. Наиболее удобно делить этот промежуток на столько же равных частей, сколько значений функции в таблице функции. Например, если значений функции 7, то разделите промежуток на 7 равных интервалов.
7. Поставьте точки на плоскости, которые соответствуют значениям аргумента и значениям функции из таблицы. Затем соедините эти точки ломаной линией.
8. Не забудьте подписать график функции и оси координат.
Построение координатной плоскости поможет визуализировать зависимость между значениями аргумента и значениями функции. Также, это поможет увидеть, как изменяется функция в заданном диапазоне аргумента.
Четвертый шаг - отметка точек на координатной плоскости

Ось Ox показывает изменение значения переменной x, а ось Oy - значение функции y. Ориентируемся на значения функции, которые мы записали в таблицу в третьем шаге, и отмечаем соответствующие точки на плоскости, соединяя их линиями.
Важно помнить, что для удобства часть точек можно пропустить, особенно если их координаты маленькие. График функции должен быть плавным и непрерывным. Поэтому, если точки слишком близки друг к другу, можно пропустить несколько их отметок на графике.
Пятый шаг - соединение точек линией
После того как мы построили таблицу значений и отметили точки на координатной плоскости, настало время соединить эти точки линиями. Для этого нужно провести линию через все точки, чтобы получилась гладкая кривая.
Чтобы соединить точки линией, нужно пронумеровать их в порядке возрастания или убывания значений аргумента. Затем отмечаем точки на графике, соответствующие значениям функции. Далее проводим линию через все отмеченные точки.
Если точки находятся на одной прямой, то линию можно провести прямо. Если точки образуют выпуклый или вогнутый контур, то линия будет соответствующего вида.
Помните, что функция может быть неопределена при некоторых значениях аргумента. В таком случае, на графике будет пропуск или разрыв линии.
- Пронумеруйте точки в порядке возрастания (убывания) значений аргумента.
- Проведите линию через все отмеченные точки.
- Учтите, что функция может быть неопределена в некоторых точках.
Шестой шаг - проверка правильности построенной таблицы функции
После того, как вы построили таблицу, важно еще раз проверить правильность вашей работы. Для этого необходимо:
| Шаг | Действие |
|---|---|
| 1 | Проверьте, что все значения x, которые вы использовали, корректно отображены в таблице. |
| 2 | Убедитесь, что значения f(x), которые вы вычислили, верны. Пересчитайте некоторые значения, чтобы убедиться в их точности. |
| 3 | Проверьте, что все цифры и знаки в таблице записаны без ошибок. Сделайте это несколько раз, чтобы не пропустить возможные опечатки. |
| 4 | Убедитесь, что таблица полностью заполнена, и вы не пропустили ни одну строку или столбец. |
| 5 | Проверьте, что таблица выглядит аккуратно и упорядоченно. Строки и столбцы должны быть выровнены, а значения должны быть четко разделены. |
Если вы нашли ошибку или неуверены в правильности таблицы, вернитесь к предыдущим шагам и проверьте свои вычисления и записи. Необходимо обнаружить и исправить любую ошибку, чтобы получить правильную таблицу функции.
Седьмой шаг - улучшение точности таблицы функции
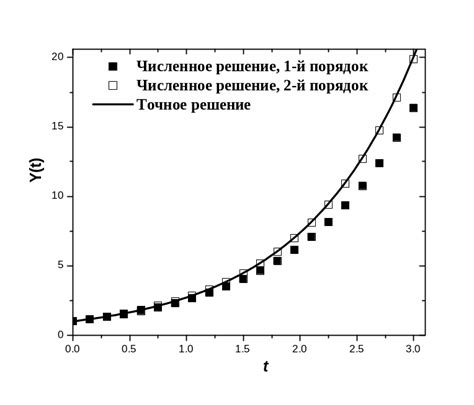
Для того чтобы сделать таблицу функции более точной, можно увеличить количество точек, в которых будет вычисляться значение функции. Это особенно важно, когда функция имеет резкие изменения или скачки. Чем больше точек мы возьмем на отрезке, тем более подробно мы сможем оценить ее поведение.
Для этого можно выбрать большее количество значений аргумента функции и вычислить соответствующие им значения. Например, вместо того, чтобы брать только 5 значений аргумента, можно взять 10 или даже 20. Таким образом, мы получим большее количество точек на графике и сможем более точно определить форму функции.
При увеличении количества точек следует учитывать пропорциональное увеличение количества строк в таблице. Необходимо добавить дополнительные строки и вычислить значения функции для новых значений аргумента. Также важно не забыть обозначить соответствующие единицы измерения для каждой строки таблицы функции.
Улучшение точности таблицы функции позволит нам более детально изучить зависимость значений функции от ее аргумента и получить более полное представление о ее поведении в разных точках.
| Аргумент | Значение функции |
|---|---|
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
| 4 | 9 |
| 5 | 11 |
| Таблица значений функции в улучшенной точности | |