Как создать уравнение в Python — подробное руководство и примеры

Python - это мощный и простой в использовании язык программирования, который предоставляет возможность создавать математические уравнения с минимальными усилиями. Независимо от того, являетесь ли вы новичком в программировании или опытным разработчиком, вы можете легко создавать и решать уравнения с помощью Python.

В этом руководстве мы рассмотрим основные шаги по созданию уравнений в Python. Во-первых, вы должны знать основы синтаксиса Python, чтобы легко писать код для уравнений. Затем мы рассмотрим различные операторы и функции, которые помогут вам создать уравнения разной сложности.

Для создания уравнений Python предлагает несколько математических операторов, таких как сложение (+), вычитание (-), умножение (*), деление (/) и возведение в степень (**). Вы также можете использовать скобки для установления приоритета операций.

Кроме того, Python предоставляет мощные математические функции и модули, которые помогут вам создавать и решать сложные уравнения. Например, вы можете использовать модуль math для работы с тригонометрическими функциями или модуль random для генерации случайных чисел в уравнениях.

Что такое уравнение?

Уравнения играют важную роль в математике и науке, поскольку они позволяют решать широкий спектр задач. Они используются для моделирования различных явлений и процессов, а также для решения практических задач в различных областях, включая физику, химию, экономику и программирование.

Уравнения могут быть линейными или нелинейными. Линейные уравнения представляют собой простые алгебраические выражения, в которых переменные входят только в первой степени. Нелинейные уравнения, в свою очередь, могут иметь более сложную форму и содержать степени переменных выше первой.

Решение уравнения заключается в нахождении значений переменных, при которых обе его стороны равны. Решение уравнений может быть аналитическим или численным. В аналитическом методе используются математические приемы, такие как алгебраические преобразования и рассуждения, чтобы выразить переменные явно. В численном методе значения переменных находятся численно путем итераций и вычислений.

Python предоставляет мощные инструменты для работы с уравнениями. С его помощью можно создавать, решать и анализировать уравнения, используя различные библиотеки и функции.

Зачем нужно создавать уравнение в Python?

Создание уравнения в Python позволяет разработчикам автоматизировать процесс решения сложных математических проблем. Python предоставляет множество математических функций и библиотек, которые могут быть использованы для создания и решения уравнений. Это позволяет программистам эффективно моделировать и анализировать различные явления и процессы.

Создание уравнений в Python также позволяет разработчикам строить графики и визуализацию результатов. Python предоставляет много инструментов для работы с графиками, что делает его идеальным инструментом для создания уравнений и визуализации их результатов. Графики могут быть использованы для лучшего понимания данных и результатов решения уравнений.

Кроме того, использование Python для создания уравнений позволяет разработчикам создавать интерактивные приложения и моделирование в реальном времени. Это открывает возможности для создания сложных и интересных проектов, таких как компьютерное моделирование физических процессов или экономических моделей.

В целом, создание уравнений в Python является важной и полезной задачей, которая позволяет разработчикам моделировать и решать сложные математические проблемы, визуализировать результаты и создавать интерактивные приложения. Это делает Python одним из наиболее популярных языков программирования для работы с уравнениями и математикой в целом.

Шаги создания уравнения в Python

Шаг 1: Импорт модуля

Первым шагом для создания уравнения в Python является импорт модуля, который позволит нам использовать математические функции и операции. Для этого мы можем использовать модуль math, который предоставляет широкий спектр математических функций.

Для импорта модуля math мы можем использовать следующий код:

Шаг 2: Задание переменных

Для создания уравнения нам необходимо задать переменные, которые будут использоваться в выражении. Переменные могут представлять собой числа или другие значения, необходимые для решения задачи.

Например, мы можем задать переменную x со значением 5 следующим образом:

Шаг 3: Написание уравнения

После задания переменных мы можем написать уравнение, используя математические операции и функции из модуля math. Уравнение может состоять из одного или нескольких выражений и операций.

Например, мы можем написать уравнение для вычисления квадратного корня из переменной x следующим образом:

Например, мы можем вывести результат вычисления квадратного корня, используя следующий код:

Теперь у вас есть все необходимые шаги для создания уравнения в Python. Вы можете изменять переменные, операции и функции, чтобы решать различные математические задачи. Удачи в программировании!

Выбор типа уравнения

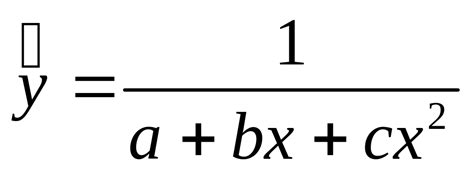
При создании уравнения в Python важно выбрать правильный тип уравнения, который соответствует поставленной задаче. В Python существует несколько типов уравнений, и каждый из них имеет свои особенности и способы решения.

Линейные уравнения:

Линейные уравнения представляют собой уравнения первой степени, в которых неизвестное значение присутствует только в первой степени. Они имеют простую форму и могут быть решены аналитически. В Python линейные уравнения могут быть записаны с помощью оператора равенства "==" или функции sympy.Eq().

Квадратные уравнения:

Квадратные уравнения представляют собой уравнения второй степени, в которых неизвестное значение присутствует во второй степени. Они могут иметь одно, два или ни одного решения. Решение квадратного уравнения можно получить с помощью формулы дискриминанта. В Python квадратные уравнения могут быть записаны с помощью функции sympy.solve().

Системы уравнений:

Системы уравнений представляют собой набор уравнений, которые нужно решить одновременно. В Python системы уравнений могут быть записаны с помощью функции sympy.solve() с несколькими уравнениями и неизвестными значениями. Решение системы уравнений может быть одним или несколькими.

Правильный выбор типа уравнения является важным шагом при решении математических задач с использованием Python. В зависимости от задачи и требуемых результатов, необходимо выбрать соответствующий тип уравнения и применить соответствующие методы и функции для его решения.

Ввод данных

Для создания уравнения в Python, требуется ввод данных. Входные данные могут быть введены с клавиатуры пользователем или считаны из файла. Для ввода данных с клавиатуры, можно использовать функцию input(). Она позволяет пользователю ввести данные с клавиатуры и сохранить их в переменную.

Пример использования функции input():

В данном примере, пользователю будет предложено ввести значение для переменных "а" и "b". Введенные значения будут сохранены в переменных "а" и "b".

Также для ввода данных можно использовать функцию sys.stdin.readline(). Она считывает строку со стандартного потока ввода и возвращает ее в виде строки.

Пример использования функции sys.stdin.readline():

В этом примере, строки из стандартного потока ввода будут сохранены в переменных "а" и "b".

После ввода данных, можно использовать их для создания уравнения в Python.

Для корректной обработки введенных данных, их необходимо преобразовать в нужный тип. Например, для числовых данных можно использовать функцию int() для преобразования строки в целое число или функцию float() для преобразования строки в число с плавающей запятой.

Пример преобразования введенных данных:

Таким образом, после преобразования введенные значения будут иметь нужный тип данных и можно будет использовать их для создания уравнения.

Расчеты

В Python можно создавать и решать различные уравнения, включая линейные, квадратные и тригонометрические уравнения. Для этого существуют специальные библиотеки, такие как SymPy, которые предоставляют функции для работы с уравнениями.

Для создания уравнения в Python можно использовать символические переменные и операторы для математических операций, такие как сложение (+), вычитание (-), умножение (*) и деление (/). Например, следующий код создает уравнение, вычисляющее сумму двух чисел:

import sympy as sp
x = sp.symbols('x')
y = sp.symbols('y')
equation = x + y
print(equation)

Результатом выполнения кода будет уравнение x + y. Если нужно решить данное уравнение, можно воспользоваться функцией solve() из библиотеки SymPy:

import sympy as sp
x = sp.symbols('x')
y = sp.symbols('y')
equation = x + y
solution = sp.solve(equation, x)
print(solution)

Результатом выполнения кода будет значение переменной x, при котором уравнение x + y равно 0.

Кроме того, можно решать более сложные уравнения, такие как квадратные и тригонометрические. Для этого также используются функции из библиотеки SymPy. Например, чтобы решить квадратное уравнение вида ax^2 + bx + c = 0:

import sympy as sp
x = sp.symbols('x')
equation = sp.Eq(2*x**2 + 3*x + 1, 0)
solution = sp.solve(equation, x)
print(solution)

Результатом выполнения кода будет список значений переменной x, удовлетворяющих квадратному уравнению.

Таким образом, благодаря библиотеке SymPy и возможности символьных вычислений в Python вы можете легко создавать и решать различные уравнения. Это позволяет проводить различные математические расчеты, которые полезны в научно-исследовательской работе, инженерии, физике и других областях.

Проверка результата:

После того, как уравнение создано и решено, всегда важно проверить полученный результат. Это позволяет удостовериться, что уравнение было правильно записано и решено без ошибок.

Для проверки результата можно вручную подставить найденные значения переменных в исходное уравнение и убедиться, что оно выполняется. Также можно использовать функции и методы Python для автоматической проверки.

Например, можно записать функцию, которая принимает значения переменных и возвращает результат исходного уравнения. Затем можно вызвать эту функцию с найденными значениями и сравнить полученный результат с ожидаемым.

• Если результаты совпадают, значит уравнение было записано и решено правильно.
• Если результаты не совпадают, нужно проверить, нет ли ошибок в исходном уравнении или при подстановке значений переменных.

Также можно использовать методы тестирования, такие как модуль unittest в Python, чтобы автоматически проверить результаты на наборе тестовых данных.

В любом случае, проверка результата является важной частью процесса создания и решения уравнения. Она позволяет убедиться в правильности полученного результата и обнаружить возможные ошибки.

x = 10
y = 5
result = x + y
print("Результат сложения:", result)

В этом примере мы создали две переменные x и y, присвоили им значения 10 и 5 соответственно, а затем сложили их и получили результат 15. С помощью функции print() мы вывели строку "Результат сложения: 15" в консоль.

x = 10
y = 5
print("Результат сложения {} и {} равен: {}".format(x, y, x + y))

Примеры создания уравнений в Python

Python предоставляет различные инструменты для создания и решения уравнений. Вот несколько примеров, как можно создать уравнение в Python:

1. Уравнение первой степени

Уравнение первой степени имеет форму ax + b = 0, где a и b - коэффициенты. В Python вы можете создать функцию для решения такого уравнения:

• def solve_linear_equation(a, b):
•     return -b/a
• x = solve_linear_equation(2, 4)
• print("Решение уравнения:", x)

2. Квадратное уравнение

Квадратное уравнение имеет форму ax^2 + bx + c = 0, где a, b и c - коэффициенты. В Python вы можете использовать модуль math для решения такого уравнения:

• import math
• def solve_quadratic_equation(a, b, c):
•     discriminant = b**2 - 4*a*c
•     if discriminant > 0:
•         x1 = (-b + math.sqrt(discriminant)) / (2*a)
•         x2 = (-b - math.sqrt(discriminant)) / (2*a)
•         return x1, x2
• elif discriminant == 0:
•         x = -b / (2*a)
•         return x
• else:
•         return "Корней нет"
• x = solve_quadratic_equation(1, -3, 2)
• print("Решение уравнения:", x)

3. Уравнение с использованием символьных вычислений

С помощью модуля sympy в Python вы можете работать с символьными выражениями и решать уравнения с неизвестными значениями:

• from sympy import symbols, Eq, solve
• x = symbols('x')
• equation = Eq(x**2 + 2*x + 1, 0)
• solutions = solve(equation, x)
• print("Решение уравнения:", solutions)

Это всего лишь несколько примеров того, как вы можете создавать уравнения в Python. В зависимости от ваших потребностей и типа уравнения, вы можете использовать различные подходы и инструменты для решения уравнений с помощью Python.