Один из наиболее широко используемых методов проверки равенства дисперсий является F-тест Фишера. Этот метод основан на сравнении дисперсий двух независимых выборок и вычисляет отношение между средним квадратическим отклонением внутри группы и средним квадратическим отклонением между группами. Если полученное значение F-статистики значительно отличается от единицы, то это говорит о наличии статистически значимого различия в дисперсии между группами.
Еще одним методом проверки равенства дисперсий является тест Левена, который основан на сравнении дисперсий двух или более групп. Этот метод более устойчив к нарушениям нормальности распределения и может применяться как для независимых, так и для зависимых выборок. Тест Левена вычисляет отношение межгрупповой и внутригрупповой дисперсии, и если полученное значение статистики значительно отличается от единицы, то это говорит о наличии статистически значимой разницы в дисперсии между группами.
Раздел 1: Определение равенства дисперсий
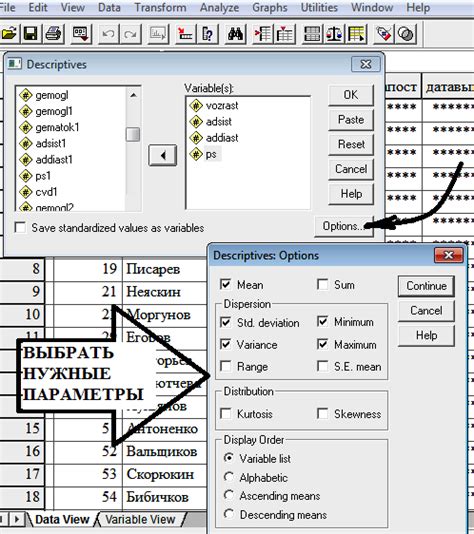
Другим методом проверки равенства дисперсий является тест Левена. Этот тест также сравнивает дисперсии двух групп, но учитывает возможное нарушение нормальности распределения данных. Тест Левена основан на анализе абсолютных отклонений значений от среднего значения.
Таким образом, определение равенства дисперсий является важной задачей в статистике. Правильный выбор метода проверки зависит от специфики данных и исследуемой проблемы.
Раздел 1.1: Что такое дисперсия

Для расчета дисперсии необходимо выполнить следующие шаги:
- Найти среднее значение набора данных. Для этого нужно сложить все значения и разделить сумму на количество значений.
- Вычислить отклонение каждого значения от среднего значения. Для этого нужно отнять среднее значение от каждого значения.
- Возвести каждое отклонение в квадрат. Это нужно для того, чтобы убрать отрицательные значения и превратить отклонения в положительные.
- Найти среднее значение квадратов отклонений. Для этого нужно сложить все квадраты отклонений и разделить сумму на количество значений.
Полученное значение является дисперсией и обозначается как σ². Чем больше значение дисперсии, тем больше разброс данных в наборе. Дисперсия также используется в других статистических методах, например, при проверке равенства дисперсий.
Раздел 1.2: Понятие равенства дисперсий
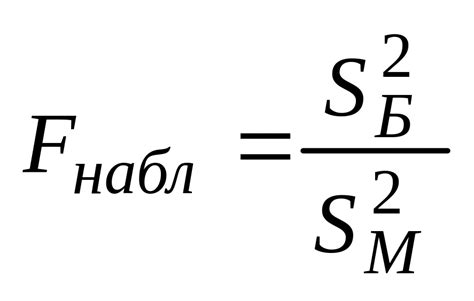
Равенство дисперсий может быть проверено с помощью различных статистических тестов, таких как тест Фишера или тест Левена. Тест Фишера основан на сравнении отношений дисперсий двух выборок, в то время как тест Левена основан на сравнении вариаций внутри и между группами данных.
Основное предположение данных при проверке равенства дисперсий является нормальное распределение. Также необходимо учитывать размер выборки, так как с увеличением размера выборки становится возможным обнаружить и незначительные различия дисперсий в данных.
Раздел 2: Значение равенства дисперсий в статистике

Значение равенства дисперсий определяется с помощью статистических тестов, таких как тест Фишера или тест Левена. Они позволяют оценить, насколько различны дисперсии в разных группах и определить, можно ли считать их равными.
Раздел 2.1: Роль равенства дисперсий в статистических тестах

В статистике существует несколько методов проверки равенства дисперсий. Один из них – тест Флигнера-Киллена. Этот тест основан на сравнении медиан отклонений от среднего значения в двух группах. Если медианы отклонений отличаются значимо, то можно предположить, что дисперсии в группах различаются.
Необходимость проверки равенства дисперсий вытекает из требований статистических тестов, которые предполагают равенство дисперсий в группах. Если дисперсии различаются, то результаты тестов могут быть искажены. Поэтому перед применением статистических тестов следует проверять равенство дисперсий и, при необходимости, использовать альтернативный метод, учитывающий эти различия.
| Метод проверки | Описание |
|---|---|
| Тест Флигнера-Киллена | Сравнивает медианы отклонений от среднего |
| Тест Левина | Сравнивает суммы квадратов отклонений от среднего |
Раздел 2.2: Влияние неравенства дисперсий на результаты исследований
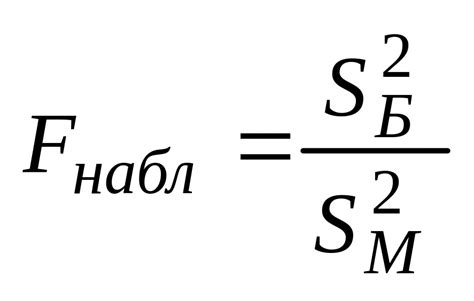
Для проведения статистических исследований важно учитывать равенство дисперсий в выборках. Неравенство дисперсий может влиять на правильность и достоверность результатов.
Если дисперсии двух выборок значительно различаются, то необходимо применять специальные методы, такие как коррекция Сatterthwaite или Вэлша. Эти методы учитывают неравенство дисперсий и позволяют получить более точные и объективные результаты исследования.
Если не учитывать неравенство дисперсий и применять обычные методы, то результаты могут быть искажены. Например, недооценка различий между выборками или неверное заключение о наличии или отсутствии статистически значимых различий.
Раздел 3: Методы проверки равенства дисперсий
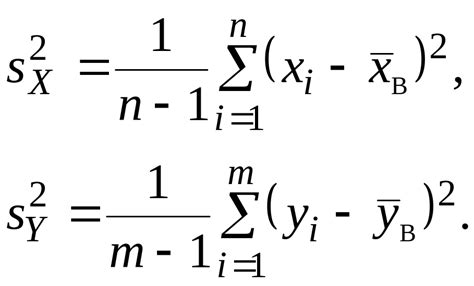
Существует несколько методов, которые позволяют проверить равенство дисперсий:
- Тест Левена. Этот метод проверяет равенство дисперсий, основываясь на сравнении средних абсолютных отклонений выборок.
- Тест Бартлетта. Данный метод основывается на анализе суммы квадратов отклонений наблюдений от общей суммы наблюдений.
- Тест Муда. Этот метод основывается на сравнении средних полуразностей выборок.
Каждый из этих методов имеет свои особенности и предположения. При выборе метода для проверки равенства дисперсий необходимо учитывать количество выборок, размер выборки и вид распределения данных.
Раздел 3.1: Тест Флингера-Килена
Шаги проведения теста:
- Сформулировать нулевую гипотезу H0: дисперсии двух выборок равны.
- Сформулировать альтернативную гипотезу H1: дисперсии двух выборок не равны.
- Вычислить отношение межгрупповой дисперсии и внутригрупповой дисперсии.
- Сравнить полученное значение с критическим значением, полученным из соответствующей таблицы (например, таблицы Фишера).
- Принять или отвергнуть нулевую гипотезу в зависимости от результата сравнения.
Тест Флингера-Килена позволяет определить, являются ли выборки статистически отличающимися по дисперсии. Этот тест может быть полезен в рамках проведения различных исследований и анализа данных, особенно при работе с несколькими выборками.
Раздел 3.2: Тест Бартлетта
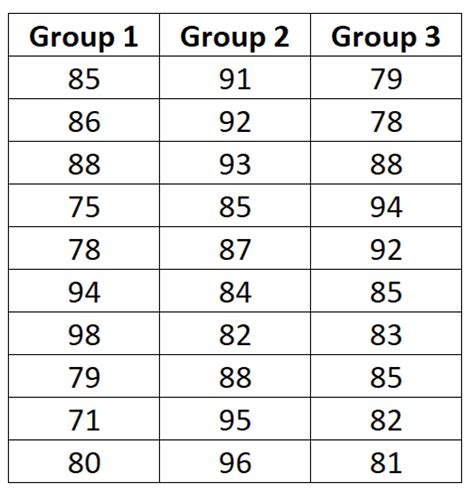
В основе теста Бартлетта лежит сравнение дисперсий между группами с помощью анализа дисперсии (ANOVA). Главная идея заключается в том, что если дисперсии равны, то средние значения рассчитанных внутригрупповых дисперсий должны быть близки к средней межгрупповой дисперсии.
Процедура теста Бартлетта включает следующие шаги:
- Сформулировать гипотезы. Нулевая гипотеза заключается в том, что дисперсии во всех группах равны, а альтернативная гипотеза предполагает, что дисперсии отличаются хотя бы в одной из групп.
- Вычислить параметр теста. Для этого необходимо рассчитать внутригрупповую и межгрупповую дисперсии, а затем сравнить их средние значения.
- Принять решение. На основе полученных результатов можно принять или отвергнуть нулевую гипотезу о равенстве дисперсий.
Тест Бартлетта имеет ряд ограничений. Во-первых, он предполагает нормальное распределение данных в каждой группе. Во-вторых, тест чувствителен к выбросам, поэтому не рекомендуется использовать его в присутствии выбросов. В-третьих, тест Бартлетта не подходит для небольших выборок.
Использование теста Бартлетта в статистическом анализе позволяет оценить равенство дисперсий в группах и принять обоснованные решения на основе полученных результатов. Это важный инструмент для исследователей и статистиков, работающих с множественными группами данных.