Система координат – это важный и неотъемлемый элемент многих научных дисциплин и технических отраслей. Но что делать, если перед вами стоит задача связать две или более различных системы координат? Не стоит паниковать! В этой статье мы рассмотрим подробную инструкцию о том, как связать системы координат и достичь желаемого результата.
Первый шаг в решении этой задачи - определить типы систем координат, которые вам необходимо связать. Это может быть 2D или 3D система координат, географическая координатная сетка или даже система координат, учитывающая вращение и масштабирование. Осведомленность о типах координатных систем поможет вам выбрать подходящий метод связывания.
Второй шаг - изучить математические основы, лежащие в основе связывания систем координат. Наиболее распространенными методами являются линейное преобразование и умножение матриц. Необходимо овладеть этими техниками, чтобы точно установить связь между системами координат и обеспечить правильное взаимодействие между ними.
Третий шаг – применить полученные знания и практические навыки для связывания выбранных систем координат. Важно понимать, что каждая связь уникальна и требует индивидуального подхода. Будьте готовы к тому, что вам придется провести дополнительные вычисления и эксперименты, чтобы достичь желаемого результата.
Итак, теперь вы знаете, как связать системы координат. Следуйте этой подробной инструкции и успешно осуществите связывание выбранных систем координат для достижения ваших целей.
Определение системы координат
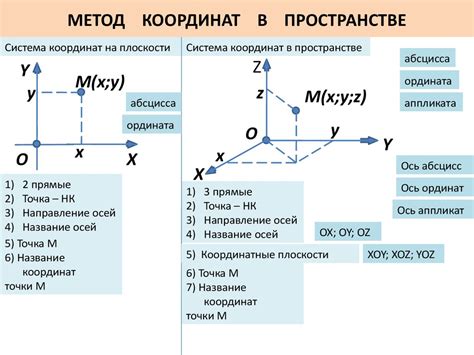
Одномерную систему координат можно представить числовой осью, на которой каждая точка имеет определенную координату. В двумерной системе координат координаты задаются парами чисел (x, y), где x - горизонтальная координата, а y - вертикальная координата. В трехмерной системе координат координаты задаются тройками чисел (x, y, z), где x - горизонтальная координата, y - вертикальная координата, а z - глубина.
В математике самая распространенная система координат - декартова система координат, в которой прямая, плоскость или пространство разбиваются на перпендикулярные оси, позволяющие удобно определить координаты точек. Кроме декартовой системы координат, существуют и другие системы координат, например, полярная система координат, сферическая система координат и цилиндрическая система координат.
Назначение связывания систем координат
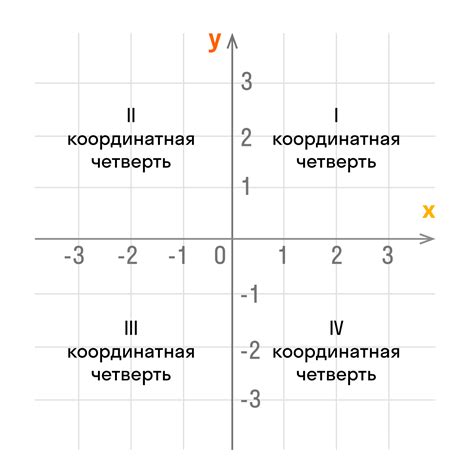
Связывание систем координат имеет множество практических применений, особенно в таких областях науки, как физика и астрономия. Например, в астрономии системы координат используются для точного определения положения звезд и других небесных объектов на небосклоне. В физике системы координат позволяют описывать движение тел в пространстве, а также моделировать различные физические явления и процессы.
Благодаря связыванию систем координат становится возможным сочетать различные методы и подходы к описанию пространственных объектов и процессов. Это позволяет решать более сложные задачи и получать более точные результаты. Также связывание систем координат способствует развитию мультискалярных и мультимодельных подходов к исследованиям и анализу данных.
Итак, назначение связывания систем координат заключается в установлении связи между различными системами координат для удобного и точного описания геометрических объектов и явлений. Это позволяет решать более сложные задачи и достигать более точных результатов в различных научных областях.
Преобразование координат
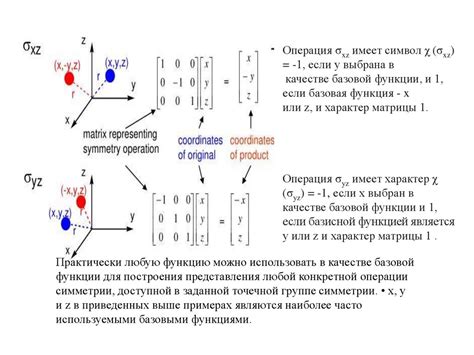
Для преобразования координат можно использовать различные методы, в зависимости от типа систем координат и требуемой точности результата. Один из самых распространенных способов преобразования - это использование математических формул и алгоритмов.
Преобразование координат может осуществляться как в двумерном, так и в трехмерном пространстве. В двумерном случае необходимо перевести значения двух координат (обычно X и Y), а в трехмерном - три координаты (X, Y и Z).
Процесс преобразования координат может включать в себя следующие шаги:
- Определение начальной и конечной систем координат.
- Изучение формул и алгоритмов, применяемых для преобразования координат в данном случае.
- Разработка программного кода или использование готовых функций и библиотек для выполнения преобразования.
- Тестирование и отладка преобразования координат для проверки его корректности и точности.
При выполнении преобразования координат необходимо учесть особенности каждой системы координат, такие как начало отсчета, направление осей, масштабирование и т. д. Также важно обращать внимание на округление значений координат для получения более точного результата.
Преобразование координат играет важную роль во многих областях, включая географию, картографию, компьютерную графику, робототехнику и другие. Оно позволяет более гибко и эффективно работать с данными, представленными в различных системах координат.
Практическое применение

Связывание систем координат имеет разнообразное практическое применение в различных областях науки и техники. Рассмотрим несколько примеров:
| Область | Применение |
|---|---|
| Геодезия | С помощью связывания систем координат можно осуществлять геодезические измерения и определять географические координаты объектов на Земле. |
| Навигация | Связывание систем координат используется для определения местоположения объектов и навигации в пространстве, например, в авиации, мореплавании или GPS-навигации. |
| Машиностроение | При разработке и проектировании машин и оборудования требуется связывание систем координат для определения положения и управления с помощью механизмов. |
| Космическая техника | В космической технике связывание систем координат необходимо для позиционирования и управления космическими аппаратами и спутниками. |
| Визуализация данных | В различных областях науки и техники визуализация данных часто требует связывания систем координат для правильного отображения информации в пространстве. |
Это только некоторые примеры применения связывания систем координат. В целом, данная техника широко применяется для работы с пространственными данными и визуализацией информации в различных областях деятельности.