Периметр круга является одной из важнейших характеристик этой геометрической фигуры, а также необходим для многих расчетов и определений в математике и физике. Знание формулы и способов вычисления периметра круга чрезвычайно полезно, особенно если вам приходится сталкиваться с задачами, связанными с окружностями.
Периметр круга – это длина окружности, то есть расстояние вокруг границы круга. Единицей измерения периметра круга является длина, обычно выраженная в единицах измерения длины, таких как метры или сантиметры. Для нахождения периметра круга используется специальная формула, которая основывается на числе π (пи).
Формула для вычисления периметра круга имеет простой вид: P = 2πr, где P - периметр, π – это число пи (примерно равно 3,14), а r - радиус окружности. Таким образом, чтобы найти периметр круга, нужно умножить число π на удвоенное значение радиуса.
Что такое периметр круга

Периметр круга является одним из основных параметров этой фигуры и определяется по формуле:
| Периметр круга (P) | = | Длина окружности (L) | = | 2 * Пи * Радиус (r) |
Где Пи - это математическая константа, приближенное значение которой равно примерно 3.14159, а радиус (r) - это расстояние от центра окружности до любой ее точки.
Зная значение радиуса, можно легко вычислить периметр круга, умножив его на 2 и на Пи. Этот параметр позволяет нам определить длину всей окружности, чтобы, например, подобрать необходимую длину трубы или шнура для обрамления круглого объекта.
Определение и основные понятия
Круг - это геометрическая фигура, которая состоит из всех точек на плоскости, находящихся на одинаковом расстоянии от данной точки, называемой центром. Расстояние от центра до любой точки на окружности круга называется радиусом круга.
Окружность - это граница круга, представляющая собой замкнутую кривую линию, состоящую из бесконечного числа точек на одинаковом расстоянии от центра круга.
Диаметр круга - это отрезок, соединяющий две точки на окружности и проходящий через центр круга. Диаметр круга равен удвоенному значению радиуса.
Формула для вычисления периметра круга: P = 2πr, где P - периметр круга, π (пи) - математическая константа, примерное значение которой равно 3,14, r - радиус круга.
Примечание: В реальности число π является иррациональным числом и поэтому имеет бесконечное число десятичных знаков. Для более точных вычислений периметра круга можно использовать более точное значение числа π, такое как 3,14159.
Формула для расчета периметра круга

Формула для расчета периметра круга:
Периметр = 2πr
- П = периметр круга
- π (пи) = математическая константа, примерное значение равно 3,14
- r = радиус круга
Для использования формулы необходимо знать радиус круга. Радиус – это расстояние от центра круга до любой точки на его границе.
Чтобы найти периметр круга, нужно умножить значение радиуса на 2π.
Например, если радиус круга составляет 5 единиц, то периметр круга равен:
Периметр = 2 * 3,14 * 5 = 31,4 единиц.
Таким образом, формула для расчета периметра круга позволяет быстро и точно найти длину его границы.
Какая формула нужна
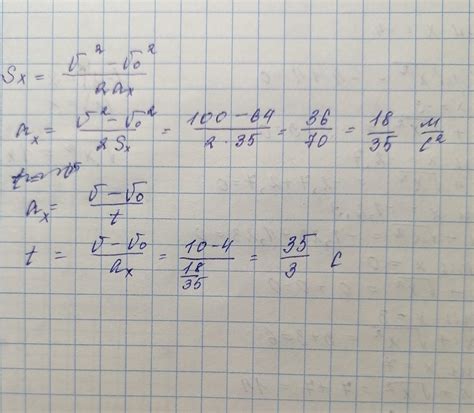
Периметр = 2 * π * радиус
где π (пи) - это математическая константа, примерно равная 3,14159. Радиус - это расстояние от центра круга до любой точки на его окружности.
Используя данную формулу, вы сможете быстро и точно вычислить периметр круга, зная только его радиус.
Как найти радиус круга
Если у вас есть диаметр круга, то радиус можно легко найти, разделив значение диаметра на 2:
Радиус = Диаметр / 2
Если у вас есть периметр круга, то радиус можно найти, используя формулу:
Радиус = Периметр / (2 x π)
Здесь π (пи) - это математическая константа, которая примерно равна 3.14 или 22/7.
Если у вас есть площадь круга, то радиус можно найти, используя формулу:
Радиус = √(Площадь / π)
Где √ обозначает квадратный корень.
Теперь, когда вы знаете несколько способов нахождения радиуса круга, вы можете использовать их в практических задачах или применить в математических вычислениях.
Методы и формулы для нахождения радиуса
1. Формула для нахождения радиуса круга по его площади:
| Формула | Обозначения |
|---|---|
| r = √(S/π) | r - радиус круга, S - площадь круга, π - число π (пи) |
2. Формула для нахождения радиуса круга по его длине окружности:
| Формула | Обозначения |
|---|---|
| r = L/(2π) | r - радиус круга, L - длина окружности, π - число π (пи) |
3. Метод измерения радиуса круга с помощью линейки:
Для измерения радиуса круга с помощью линейки необходимо провести от центра круга до его периферии прямую линию. Затем измерить расстояние между центром и периферией с помощью линейки. Полученная величина будет радиусом круга.
Каждый из этих методов и формул является эффективным и позволяет находить радиус круга в разных ситуациях. Выбор метода зависит от доступных данных и удобства его использования.
Как найти диаметр круга
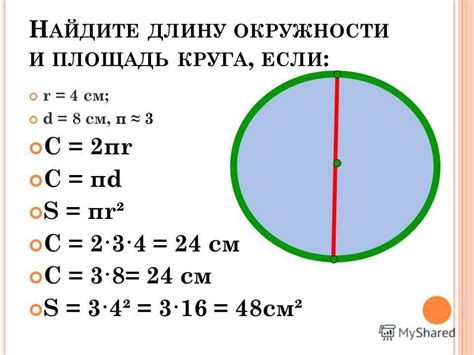
- Если известен радиус:
- Радиус - это расстояние от центра круга до его границы. Диаметр будет в два раза больше радиуса.
- Диаметр = 2 * Радиус
- Периметр - это длина границы круга. Диаметр будет равен периметру, деленному на число "π" (пи).
- Диаметр = Периметр / Пи
Например, если радиус круга равен 5 см, то диаметр будет 10 см (5 * 2).
Если периметр круга равен 20 см и число "π" примем за 3.14, то диаметр будет примерно равен 6.37 см (20 / 3.14).
Теперь вы знаете два способа найти диаметр круга, используя информацию о радиусе или периметре. Эта информация может быть полезной при решении задач по геометрии и в других сферах, где требуется работа с кругами.
Методы и формулы для нахождения диаметра
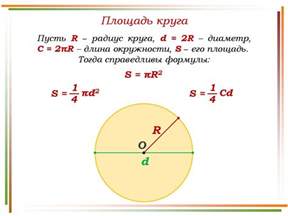
Существует несколько методов и формул для нахождения диаметра круга.
1. Измерение диаметра с помощью линейки: Самый простой способ найти диаметр круга - это измерить его длину с помощью линейки. Положите линейку на окружность так, чтобы она проходила через ее центр, и запишите измеренное значение.
2. Использование радиуса: Диаметр круга можно вычислить, зная его радиус. Радиус - это расстояние от центра окружности до ее любой точки. Диаметр равен удвоенному значению радиуса. Формула для вычисления диаметра по радиусу: диаметр = 2 * радиус.
3. Использование площади круга: Если известна площадь круга, можно найти его диаметр. Для этого нужно использовать формулу для площади круга: площадь = Pi * радиус^2. Зная площадь, можно выразить радиус по формуле радиус = √(площадь / Pi) и затем удвоить его, чтобы найти диаметр.
Выберите подходящий для вас метод и формулу для нахождения диаметра круга в зависимости от предоставленных условий и данных о круге.
Как найти площадь круга

Площадь круга можно вычислить с помощью формулы:
| S = π * r2 |
где:
- S - площадь круга;
- π (пи) - математическая константа, примерно равная 3.14159;
- r - радиус круга.
Для вычисления площади круга необходимо умножить квадрат радиуса на число π.
Например, если радиус круга равен 5 см, то площадь круга будет равна:
| S = 3.14159 * 52 = 3.14159 * 25 = 78.53975 см2 |
Таким образом, площадь круга с радиусом 5 см равна 78.53975 см2.