Неровные фигуры могут представлять собой сложные и несимметричные объекты, которые не всегда удобно измерять и анализировать. Но существуют методы и формулы, которые позволяют рассчитать их периметр и площадь точно и эффективно. Это особенно полезно, когда необходимо провести строительные работы или выполнить задачи в геометрии.
Периметр неровной фигуры определяется как сумма длин всех её сторон. Для рассчета периметра можно использовать геометрические инструменты, такие как линейка или сантиметровая лента. Но если фигура имеет сложную форму или большое количество сторон, то измерение каждой стороны может быть неудобным и затратным во временном плане.
Для таких случаев существуют различные методы аппроксимации и алгоритмы, которые позволяют более точно рассчитать периметр неровной фигуры. Одним из них является метод, основанный на использовании математических моделей и анализе контура фигуры. Этот метод позволяет разбить фигуру на более простые геометрические формы и использовать соответствующие формулы для рассчета периметра.
Площадь неровной фигуры определяется как пространство, занимаемое этой фигурой на плоскости. Рассчитать площадь фигуры можно с помощью различных методов, в зависимости от её формы. Используя приближенные методы, аппроксимации или численные алгоритмы, можно достичь достаточно высокой точности при расчете площади сложных фигур.
В данной статье мы рассмотрим несколько популярных методов и формул для расчета периметра и площади неровных фигур. Познакомимся с основными принципами и шагами, которые необходимо выполнить, чтобы получить точные и надежные результаты. Эти знания помогут вам выполнять задачи в геометрии и строительстве, а также в повседневной жизни, когда необходимо измерить и рассчитать параметры сложных фигур.
Методы расчета периметра и площади неровных фигур
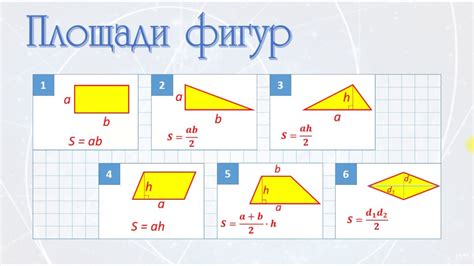
Одним из методов является разбиение неровной фигуры на более простые геометрические формы, такие как треугольники, прямоугольники или круги. Затем для каждой простой фигуры рассчитывается отдельно периметр и площадь, а затем результаты суммируются.
Еще одним методом является использование аппроксимации неровной фигуры более правильной геометрической формой. Например, если неровная фигура имеет форму правильного треугольника, то ее периметр и площадь можно рассчитать по соответствующим формулам для треугольника.
Для некоторых неровных фигур существуют специальные формулы расчета периметра и площади. Например, для эллипса с заданными полуосями существуют формулы, позволяющие точно рассчитать его периметр и площадь.
Однако для более сложных и нестандартных неровных фигур порой необходимо использовать численные методы и компьютерные программы. Например, метод Монте-Карло может использоваться для аппроксимации площади фигуры путем генерации случайных точек и проверки их принадлежности фигуре.
Важно отметить, что точность расчета периметра и площади неровных фигур зависит от выбранного метода и аппроксимации. Чем более простой и близкой к фигуре выбрана аппроксимация, тем более точными будут результаты.
Выбор метода расчета периметра и площади неровных фигур зависит от конкретной фигуры и требований к точности. Для простых фигур можно использовать специальные формулы, а для более сложных - методы аппроксимации или численные методы.
Аппроксимация фигуры прямоугольниками
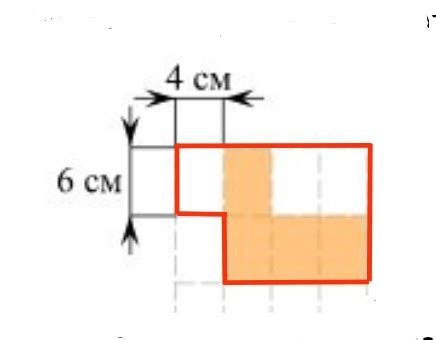
Для аппроксимации фигуры прямоугольниками необходимо разделить ее на прямоугольные ячейки таким образом, чтобы каждая ячейка имела примерно одинаковую площадь. Для этого можно использовать различные методы, например, метод равномерного разбиения или метод динамического разбиения на основе плотности точек.
После разбиения фигуры на прямоугольные ячейки можно вычислить площадь каждой ячейки, сложить их и получить приближенное значение площади всей фигуры. Для вычисления периметра можно использовать аналогичный подход - вычислить периметр каждой ячейки и сложить их.
Важно отметить, что аппроксимация фигуры прямоугольниками является приближенным методом и точность результата будет зависеть от величины ячеек, которые используются для разбиения. Чем меньше размеры ячеек, тем более точный будет результат, но при этом вычислительная сложность метода будет увеличиваться.
Аппроксимация фигуры прямоугольниками широко используется в различных областях, включая компьютерную графику, анализ изображений и географические информационные системы. Она позволяет упростить вычисления и получить приближенные значения площади и периметра сложных форм с минимальными затратами.
Использование дифференциальной геометрии

Вычисление периметра неровной фигуры с помощью дифференциальной геометрии основано на вычислении длины кривой. Кривая представляется в виде параметрического уравнения, где каждая точка на кривой задается вектором из двух функций, описывающих координаты этой точки. Для вычисления длины кривой можно применить формулу длины дуги, которая зависит от первой производной функций, описывающих кривую.
Для вычисления площади неровной фигуры с помощью дифференциальной геометрии можно использовать понятие площади поверхности. Поверхность представляется в виде параметрического уравнения, где каждая точка на поверхности задается вектором из трех функций, описывающих координаты этой точки. Для вычисления площади поверхности можно применить формулу для вычисления площади элемента поверхности, которая зависит от первых производных функций, описывающих поверхность.
Использование дифференциальной геометрии для рассчета периметра и площади неровной фигуры позволяет получить более точные и адекватные результаты, особенно для сложных и неоднородных форм. Однако, для применения этих методов необходимо иметь знания в области дифференциальной геометрии и математического анализа.
Метод монте-карло для определения площади фигуры

Для применения метода монте-карло необходимо выполнить следующие шаги:
- Выбрать область, в которой находится фигура. Область должна быть достаточно большой, чтобы в нее могли попасть все точки фигуры.
- Создать случайные точки внутри области. Количество точек зависит от требуемой точности результата. Обычно используется несколько тысяч точек.
- Проверить, сколько из созданных точек попадают внутрь фигуры. Для этого необходимо выполнить проверку, принадлежит ли каждая точка фигуре или нет.
- Рассчитать площадь фигуры по формуле: площадь фигуры = (число точек внутри фигуры / общее число точек) * площадь области.
Метод монте-карло особенно полезен при определении площади сложных неровных фигур, для которых сложно или невозможно использовать аналитические методы. Он позволяет получать достаточно точные результаты при сравнительно небольших затратах вычислительных ресурсов.
Однако, следует учитывать, что точность результата метода монте-карло зависит от количества созданных случайных точек. Чем больше точек создается, тем более точный результат может быть получен.
| Преимущества метода монте-карло | Недостатки метода монте-карло |
|---|---|
| Применим для сложных неровных фигур | Требует большого количества случайных точек для достаточной точности |
| Достаточно точный результат при небольших затратах вычислительных ресурсов | Точность результата зависит от количества созданных случайных точек |
| Позволяет обойти сложности использования аналитических методов |