Дифференциалы являются важным инструментом в математике, особенно в области дифференциальных уравнений. Они позволяют нам рассчитывать изменения функций в конкретных точках. В данной статье мы рассмотрим, как найти дифференциал в точке и предоставим несколько примеров для лучшего понимания.
Прежде всего, давайте определимся, что такое дифференциал. Для функции одной переменной дифференциалом является дифференциал функции, т.е. малая приращение функции, полученное в результате незначительного изменения ее аргумента. Дифференциал обозначается символом "d", аргумент функции - переменной x, а функцию - символом f(x). Иными словами, дифференциал это частная производная функции по переменной, умноженная на дифференциал переменной.
Чтобы найти дифференциал в точке, мы должны знать значение производной функции в данной точке. Производная показывает наклон касательной к кривой в этой точке. Зная значение производной, мы можем найти дифференциал по следующей формуле: дифференциал равен производной, умноженной на малое приращение аргумента.
Для наглядности рассмотрим пример. Пусть дана функция f(x) = x^2. Найдем дифференциал функции в точке x_0 = 3. В данном случае, производная функции f(x) равна f'(x) = 2x. Подставляя значение 3 вместо x, получим производную f'(3) = 2 * 3 = 6. Затем, умножим значение производной на малое приращение аргумента dx. Предположим, что dx = 0.1. Тогда дифференциал df(x) в точке x_0 = 3 будет равен 6 * 0.1 = 0.6.
Дифференциал в точке: что это и как его найти?

Для нахождения дифференциала в точке необходимо сначала найти производную функции в этой точке. Производная функции в точке - это скорость изменения функции в данной точке. Зная производную, можно найти уравнение касательной прямой к графику функции в этой точке. Дифференциал в точке можно получить, используя следующую формулу:
dy = f'(x) * dx
Где dy - дифференциал функции, f'(x) - производная функции, а dx - независимое изменение аргумента функции.
Рассмотрим пример:
function f(x) {
return x^2; // Возведение числа в квадрат
}
var x = 2; // Заданная точка
var dx = 0.1; // Изменение аргумента
var dy = f'(x) * dx; // Вычисление дифференциала
console.log("Дифференциал в точке " + x + " равен " + dy);
Таким образом, дифференциал в точке позволяет оценить изменение функции при небольшом изменении аргумента и играет важную роль в математическом анализе.
Определение дифференциала в точке

Математический дифференциал обозначается как d и расшифровывается как дифференциал. Он представляет собой инкремент функции f(x) в окрестности точки x, где изменение x очень мало. Дифференциал можно представить в виде отношения двух переменных dx и dy, таким образом:
| d | = | dy | / | dx |
Дифференциал функции может быть выражен через производную функции в данной точке. Формула для вычисления дифференциала в точке x выглядит следующим образом:
| d | = | f'(x) | * | dx |
Где f'(x) представляет собой производную функции f в точке x. Дифференциал позволяет описывать, как значение функции f изменяется в окрестности данной точки.
Примером использования дифференциала является вычисление приближенного значения функции вблизи данной точки. Предположим, у нас есть функция f(x) = x^2, и мы хотим найти значение функции при x = 1. Мы можем использовать дифференциал, чтобы приближенно рассчитать значение:
| df | = | f'(x) | * | dx |
| df | = | 2x | * | dx |
| df | = | 2 | * | dx |
Теперь, если мы возьмем очень малое значение dx, например, dx = 0.1, мы можем приближенно рассчитать значение функции при x = 1:
| df | = | 2 | * | 0.1 |
| df | = | 0.2 |
Дифференциал в точке имеет широкое применение в анализе функций, оптимизации и физических задачах. Он позволяет аппроксимировать функции и рассчитывать их изменения вблизи заданной точки.
Методы нахождения дифференциала в точке
Существует несколько методов нахождения дифференциала в точке для заданной функции. Каждый из этих методов имеет свои особенности и применяется в различных ситуациях. Рассмотрим некоторые из них:
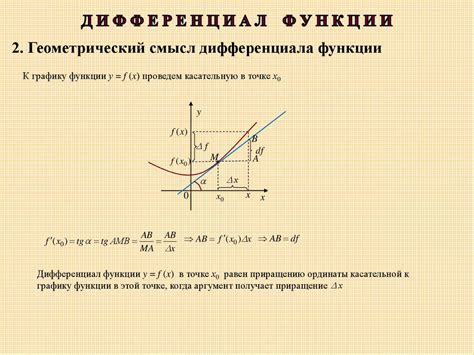
- Геометрический метод: данный метод основан на графическом представлении функции. Дифференциал в точке можно рассчитать по формуле дифференцирования. Приближенное значение дифференциала можно найти с помощью касательной к графику функции в данной точке. Расстояние от точки до касательной будет приближенным значением дифференциала.
- Аналитический метод: данный метод основан на использовании формул дифференцирования функций. Для нахождения дифференциала в точке нужно взять первую производную функции по переменной, заменить эту переменную на значение в данной точке, и вычислить полученное выражение.
- Численные методы: данные методы основаны на численном приближении дифференциала. Одним из наиболее распространенных методов является метод конечных разностей. Для этого необходимо выбрать малое приращение x, вычислить значение функции в точке x+h и x-h, а затем найти разность этих значений и разделить на 2h.
- Символьные методы: данный метод основан на использовании символьных вычислений. Используя символьные математические пакеты, можно вычислить дифференциалы различных функций в точке, основываясь на их аналитическом представлении.
Выбор метода нахождения дифференциала в точке зависит от конкретной задачи и имеющихся данных. В различных ситуациях разные методы могут быть предпочтительными.
Примеры нахождения дифференциала в точке

Рассмотрим несколько примеров, чтобы лучше понять, как найти дифференциал в точке.
Пример 1:
Пусть дана функция f(x) = x^2 - 3x. Необходимо найти дифференциал этой функции в точке x = 2.
Для этого сначала найдем производную функции f(x). Производная f'(x) = 2x - 3.
Теперь мы можем найти значение производной в точке x = 2: f'(2) = 2(2) - 3 = 1.
Дифференциал функции f(x) в точке x = 2 будет равен df = f'(2)dx = 1dx = dx.
Пример 2:
Рассмотрим функцию g(x) = sin(x). Найдем дифференциал этой функции в точке x = π/4.
Производная g'(x) = cos(x).
Значение производной в точке x = π/4: g'(π/4) = cos(π/4) = √2/2.
Дифференциал функции g(x) в точке x = π/4 будет равен dg = g'(π/4)dx = (√2/2)dx.
Пример 3:
Для функции h(x) = ln(x) найдем дифференциал в точке x = 3.
Производная h'(x) = 1/x.
Значение производной в точке x = 3: h'(3) = 1/3.
Дифференциал функции h(x) в точке x = 3 равен dh = h'(3)dx = (1/3)dx.
Таким образом, нахождение дифференциала в точке требует нахождения производной функции и вычисления значения производной в данной точке.