Диагональ куба - это расстояние между двумя противоположными вершинами его граней. Зная площадь поверхности куба, мы можем вычислить его диагональ. Но как это сделать?
Прежде всего, нужно знать формулу для вычисления площади поверхности куба. Площадь поверхности куба равна удвоенной площади одной его грани. Таким образом, площадь поверхности S можно выразить формулой S = 6a², где a - длина ребра куба.
Чтобы вычислить длину ребра куба, необходимо изучить формулу для вычисления объема куба. Объем куба V равен a³, где a - длина ребра куба. Таким образом, длину ребра куба можно выразить формулой a = ∛V.
Теперь, когда у нас есть длина ребра куба a, мы можем найти его диагональ. Диагональ куба можно вычислить с помощью теоремы Пифагора для прямоугольного треугольника, образованного диагональю, одной его гранью и его диагональю проекции.
Диагональ куба: формула и инструкция
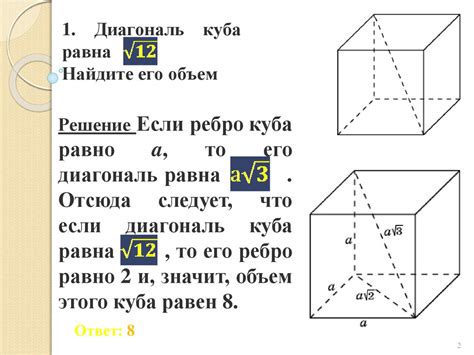
Если известна площадь поверхности куба и необходимо найти его диагональ, можно воспользоваться специальной формулой. Эта формула связывает диагональ куба и его площадь поверхности:
Диагональ куба = √(площадь поверхности куба / 3)
Для решения этой задачи следуйте следующей инструкции:
- Найдите площадь поверхности куба. Для этого умножьте длину одной из сторон куба на самого себя, а затем умножьте полученный результат на 6 (поскольку у куба 6 граней).
- Полученную площадь поверхности куба разделите на 3. Это даст вам значение, которое нужно извлечь корнем квадратным.
- Извлеките корень квадратный из полученного числа. Это и будет диагональ куба.
Теперь, зная площадь поверхности куба, вы можете легко определить его диагональ, следуя этой простой формуле и инструкции.
Что такое диагональ?

Диагональ куба играет важную роль в определении его геометрических параметров, таких как объем и площадь поверхности. Например, используя длину диагонали куба, можно найти его площадь поверхности по формуле, умножая длину диагонали на саму себя и умножая результат на 3.
Подсчет диагонали куба может быть полезен при решении различных задач в геометрии, а также при проектировании и строительстве. Поэтому знание, как узнать диагональ куба по площади его поверхности, может быть полезным для всех, кто интересуется геометрией или работает с трехмерными фигурами.
Расчет диагонали куба
Для расчета диагонали куба по площади его поверхности, можно использовать следующий алгоритм:
| Шаг | Действие |
|---|---|
| 1. | Найти площадь поверхности куба. |
| 2. | Подставить значение площади поверхности в формулу для нахождения диагонали куба. |
| 3. | Вычислить значение диагонали куба по формуле. |
| 4. | Получить итоговое значение диагонали куба. |
Используя этот алгоритм, можно точно определить диагональ куба по известной площади его поверхности. Важно помнить, что площадь поверхности куба и его диагональ - это взаимосвязанные параметры, и изменение одного из них влечет изменение другого.
Какие данные нужны для расчета диагонали куба?

Если известна площадь поверхности куба, то формула для нахождения длины его стороны будет a = √(S/6).
Диагональ куба вычисляется с помощью теоремы Пифагора. Если известна длина стороны куба (a), то диагональ (d) будет равна d = a√3.
Итак, для расчета диагонали куба, необходимо знать площадь поверхности или длину стороны куба. По этим данным можно использовать соответствующие формулы и получить результат.
Формула расчета диагонали куба

Для того чтобы узнать диагональ куба, можно воспользоваться формулой, которая основана на известной площади поверхности.
Итак, чтобы найти диагональ куба, нужно выполнить следующие шаги:
- Найдите площадь поверхности куба. Это можно сделать путем умножения длины ребра на само себя и на шесть (так как у куба шесть граней).
- Полученную площадь поверхности умножьте на 2 и возведите в квадрат.
- Затем извлеките квадратный корень из полученного значения.
Это и будет диагональ куба.
Формула для расчета диагонали куба выглядит следующим образом:
Диагональ = √(2 * (площадь поверхности куба))
Таким образом, расчет диагонали куба по площади поверхности требует выполнения нескольких простых математических операций.
Как узнать площадь поверхности куба?
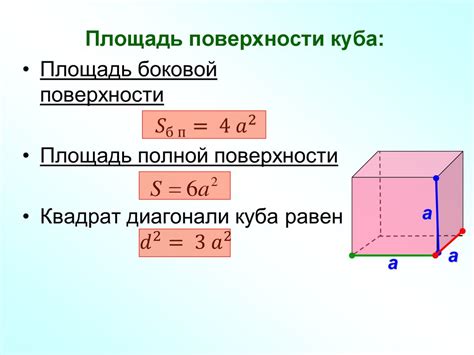
Площадь поверхности куба может быть вычислена с помощью формулы, которая учитывает длину ребра куба.
1. Определите длину ребра куба.
2. Возведите длину ребра куба в квадрат, чтобы найти площадь грани (Sг).
3. Умножьте площадь грани на 6, так как у куба 6 граней, чтобы найти общую площадь поверхности куба (Sп).
Формула для вычисления площади поверхности куба:
- Sг = a², где a - длина ребра куба.
- Sп = 6 * Sг, где Sп - площадь поверхности куба.
Пример вычисления площади поверхности куба:
- Пусть длина ребра куба a = 4 см.
- Вычисляем площадь грани: Sг = 4² = 16 см².
- Умножаем площадь грани на 6: Sп = 6 * 16 = 96 см².
Таким образом, площадь поверхности данного куба равна 96 см².
Обратная задача: как по площади поверхности найти диагональ куба?
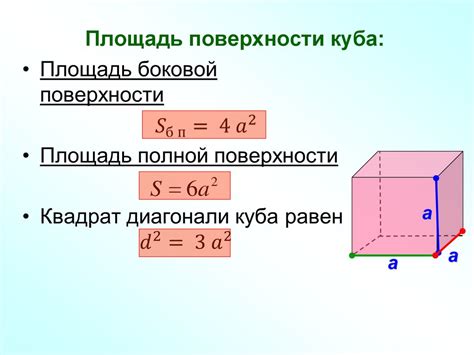
В предыдущей статье мы рассмотрели, как найти площадь поверхности куба при известной длине его диагонали. Теперь рассмотрим обратную задачу: как по заданной площади поверхности найти длину диагонали куба.
Для решения этой задачи нам понадобится использовать формулу для площади поверхности куба:
S = 6 * a2, где a - длина ребра куба.
Давайте представим, что нам известна площадь поверхности куба, например, S = 96. Наша задача - найти длину диагонали куба.
Для начала найдем длину ребра a по формуле:
a = √(S / 6).
Подставим значение площади поверхности куба в эту формулу:
a = √(96 / 6).
Выполним расчет:
√(96 / 6) = √16 = 4.
Таким образом, длина ребра куба равна a = 4.
Для решения обратной задачи нам необходимо найти длину диагонали куба. В кубе диагональ проходит от одного угла до противоположного угла через его центр. Диагональ куба можно найти по его ребру, используя формулу для диагонали куба:
d = a√3, где d - длина диагонали куба
Подставим значение длины ребра куба в эту формулу:
d = 4 * √3.
Окончательно, после выполнения расчета, получаем:
4 * √3 ≈ 6.93.
Таким образом, длина диагонали куба при заданной площади поверхности S = 96 составляет приблизительно d ≈ 6.93.
Теперь вы знаете, как по площади поверхности куба найти длину его диагонали. Удачи в расчетах!
Подробная инструкция по расчету диагонали куба

Расчет диагонали куба может быть полезным при выполнении задач, связанных с геометрией, строительством или интерьерным дизайном. Для того чтобы узнать диагональ куба, необходимо знать его площадь поверхности. В данной инструкции представлены шаги, которые помогут вам точно определить длину диагонали куба по известной площади поверхности.
- Определите площадь поверхности куба. Площадь поверхности куба вычисляется по формуле: S = 6 * a^2, где S - площадь поверхности, а - длина стороны куба.
- Найдите длину стороны куба. Для этого необходимо извлечь квадратный корень из площади поверхности, разделенной на 6: a = √(S/6).
- Рассчитайте диагональ куба. Диагональ куба вычисляется по формуле: d = √(3) * a, где d - длина диагонали куба, a - длина стороны куба.
Применяйте эту инструкцию, чтобы быстро и точно определить длину диагонали куба по известной площади поверхности. Если вам потребуется узнать другие параметры куба, например, объем или плотность, используйте соответствующие формулы и методы расчетов.
Примеры решения задач по диагонали куба

Ниже представлены несколько примеров решения задач, связанных с определением диагонали куба по известной площади поверхности:
- Задача 1
- Задача 2
- Задача 3
Дано: площадь поверхности куба равна 96 квадратных сантиметров.
Решение: для начала найдем длину одной стороны куба. Для этого воспользуемся формулой площади поверхности куба:
S = 6a^2, где S - площадь поверхности, а - длина стороны.
Из этой формулы выражаем a:
a = √(S/6).
Теперь, зная длину одной стороны куба, найдем длину его диагонали. Для этого воспользуемся теоремой Пифагора:
d = √(a^2 + a^2 + a^2), где d - диагональ, a - длина стороны.
Подставляем значение a:
d = √(3a^2).
И окончательно получаем:
d = √(3(√(S/6))^2).
Рассчитываем значение диагонали:
d = √(3(√(96/6))^2) ≈ 8.77 сантиметров.
Дано: площадь поверхности куба равна 150 квадратных метров.
Решение: аналогично предыдущей задаче, найдем длину одной стороны куба по формуле:
a = √(S/6).
Подставляем значение площади:
a = √(150/6) ≈ 4.08 метра.
Теперь найдем длину диагонали по формуле:
d = √(3(√(S/6))^2).
Подставляем значение стороны:
d = √(3(√(150/6))^2) ≈ 7.46 метров.
Дано: площадь поверхности куба равна 54 квадратных дециметра.
Решение: процесс решения такой же, как и в предыдущих задачах. Сначала находим длину стороны:
a = √(S/6).
Подставляем значение площади:
a = √(54/6) ≈ 2.31 дециметра.
Затем находим длину диагонали куба:
d = √(3(√(S/6))^2).
Подставляем значение стороны:
d = √(3(√(54/6))^2) ≈ 4.22 дециметра.
Следуя подобным шагам, можно решить любую задачу, связанную с нахождением диагонали куба по площади его поверхности.