Окружность кольца представляет собой непрерывную кривую, образованную неправильной фигурой, которая отличается от обычной окружности наличием внутреннего и внешнего радиусов. Нахождение длины окружности кольца является важной задачей в геометрии, а также в различных областях применения, включая строительство, инженерию и дизайн.
Существует несколько способов нахождения длины окружности кольца. Один из самых простых способов - использование формулы, основанной на радиусах внутренней и внешней окружностей. Для этого необходимо сложить длины окружностей обоих радиусов и умножить полученную сумму на два. Таким образом, формула для нахождения длины окружности кольца записывается как 2π(R1 + R2), где R1 - радиус внутренней окружности, R2 - радиус внешней окружности, а π - математическая константа, примерно равная 3.14159.
Если известны длина окружности одной из окружностей и разность радиусов внутренней и внешней окружностей, то можно найти длину окружности кольца по формуле 2πR, где R - полусумма радиусов внутренней и внешней окружностей. Этот метод удобен в ситуациях, когда измерение одной из окружностей производится с большей точностью или проще, чем измерение обеих окружностей.
Понятие длины окружности кольца

Длина окружности кольца является суммой длин внешней и внутренней окружностей. Для вычисления длины окружности кольца необходимо знать радиусы этих окружностей.
Формула для вычисления длины окружности кольца следующая:
- Для внешней окружности:
2 * π * R1, гдеR1- радиус внешней окружности - Для внутренней окружности:
2 * π * R2, гдеR2- радиус внутренней окружности
Общая длина окружности кольца определяется по формуле:
2 * π * (R1 + R2)
Здесь π (пи) - это математическая константа, приближенное значение которой равно 3,14.
Зная радиусы внешней и внутренней окружностей, можно использовать указанную формулу для вычисления длины окружности кольца, что позволяет определить длину периметра кольца и использовать эту информацию в различных приложениях и задачах геометрии и инженерии.
Зависимость длины окружности от радиуса

| Радиус (R) | Длина окружности (C) |
|---|---|
| 1 | 6.28 |
| 2 | 12.57 |
| 3 | 18.85 |
| 4 | 25.13 |
| 5 | 31.42 |
Из таблицы видно, что длина окружности пропорциональна радиусу. Каждый раз, когда радиус увеличивается на 1, длина окружности увеличивается на примерно 6.28 (или около этого значения). Это связано с тем, что длина окружности можно выразить через число пи (π), которое приближенно равно 3.14 или 22/7. Таким образом, формула для расчета длины окружности становится C = 2πR, где C - длина окружности, π - число пи, а R - радиус.
Знание зависимости длины окружности от радиуса позволяет быстро и точно рассчитать длину окружности и решить различные задачи, связанные с геометрией и физикой. Например, используя эту формулу, можно определить длину провода, необходимую для обмотки катушки с определенным радиусом, или расчитать путь, пройденный автомобилем по окружности определенного радиуса.
Способ 1: Использование формулы длины окружности

Для того чтобы узнать длину окружности кольца, можно воспользоваться формулой. Предположим, что радиус внутренней окружности равен R1, а радиус внешней окружности равен R2. Тогда формула для расчета длины окружности выглядит следующим образом:
Длина окружности = 2 * π * R
где π (пи) – это математическая константа, приближенное значение которой равно 3.14159...
Применяя эту формулу, можно легко вычислить длину окружности кольца, зная значения радиусов внутренней и внешней окружностей.
Способ 2: Использование угла и радиуса
Для начала, нужно измерить или найти угол в градусах между двумя радиусами кольца. Затем, следует найти значение радиуса кольца. С помощью этих данных можно использовать следующую формулу для расчета длины окружности:
Длина окружности = 2π * радиус * (угол/360)
где π (пи) - математическая константа, приближенное значение которой равно 3.1416.
Примечание: Если известна длина дуги, можно использовать эту формулу для нахождения радиуса кольца. Для этого формула преобразуется следующим образом:
Радиус = (Длина дуги * 360) / (2π * угол)
Используя данный способ расчета, можно определить длину окружности кольца при известных значении угла и радиуса.
Вычисление длины окружности с помощью Пи
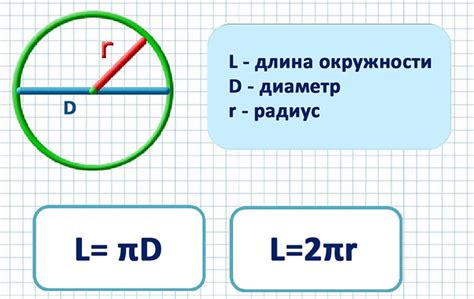
Длина окружности = 2πr
где π (пи) - это математическая константа, которая равна примерно 3,14159 или 22/7. Рекомендуется использовать более точное значение числа Пи, например, 3,141592653589793.
Для вычисления длины окружности с помощью формулы с Пи нужно знать значение радиуса кольца. Радиус обычно измеряется в единицах длины, например, в метрах, сантиметрах или дюймах.
Пример:
- Предположим, у нас есть кольцо с радиусом 5 сантиметров (r = 5 см).
- Для вычисления длины окружности с помощью формулы с Пи, вставим значение радиуса в формулу: Длина окружности = 2πr = 2 * 3,141592653589793 * 5 = 31,4159265358979 см.
- Таким образом, длина окружности равна примерно 31,42 сантиметра.
Используя формулу с Пи, можно вычислить длину окружности кольца в любых единицах измерения радиуса. С помощью этой формулы можно также вычислить площадь кольца и другие параметры окружности.
Примеры расчета длины окружности кольца

Для расчета длины окружности кольца необходимо знать его внешний и внутренний радиусы. Давайте рассмотрим несколько примеров расчета:
Пример 1:
Допустим, внешний радиус кольца составляет 10 см, а внутренний радиус - 5 см. Найдем длину окружности:
Для начала, воспользуемся формулой длины окружности:
C = 2πr
Для внешней окружности:
C1 = 2πr1 = 2π(10) ≈ 62.83 см
Для внутренней окружности:
C2 = 2πr2 = 2π(5) ≈ 31.42 см
Теперь, чтобы найти длину окружности кольца, нужно вычесть из длины внешней окружности длину внутренней окружности:
Cк = C1 - C2 = 62.83 - 31.42 ≈ 31.41 см
Пример 2:
Рассмотрим кольцо, у которого внешний радиус равен 8 мм, а внутренний радиус - 4 мм. Выполним аналогичные расчеты:
Для внешней окружности:
C1 = 2πr1 = 2π(8) ≈ 50.27 мм
Для внутренней окружности:
C2 = 2πr2 = 2π(4) ≈ 25.13 мм
Длина окружности кольца:
Cк = C1 - C2 = 50.27 - 25.13 ≈ 25.14 мм
Таким образом, длина окружности кольца составляет примерно 31.41 см в первом примере и 25.14 мм во втором примере.
Используя данную информацию, можно легко рассчитать длину окружности кольца при заданных радиусах.