Окружность - одна из основных геометрических фигур, часто встречающаяся в различных областях знаний. Хорда - это отрезок, соединяющий две точки на окружности. Важно знать, как вычислить длину хорды окружности, чтобы применять это знание в задачах и решать геометрические проблемы.
Длина хорды окружности зависит от ее положения внутри окружности и угла, натянутого между концами хорды. Существует несколько способов вычисления длины хорды окружности. Один из наиболее простых и универсальных методов основан на использовании радиуса окружности и величины центрального угла, образованного хордой.
Для вычисления длины хорды окружности можно воспользоваться формулой, которая связывает радиус окружности, центральный угол и длину хорды. При правильном использовании этой формулы можно точно определить длину хорды, даже если изначально даны только радиус и угол. Важно помнить, что угол измеряется в радианах, а не в градусах.
Окружность и хорда: определение и связь между ними
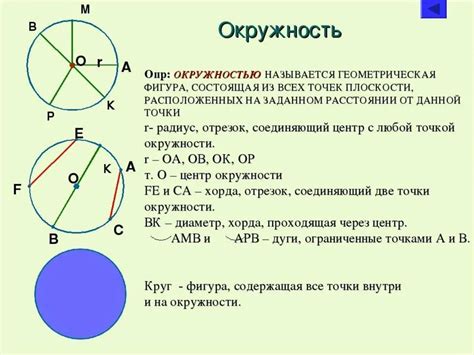
Хорда окружности - это отрезок, соединяющий две точки на окружности. Она является одной из основных составляющих окружности и имеет свои уникальные свойства. При изучении окружностей часто возникает необходимость вычисления длины хорды, чтобы решить различные задачи.
Связь между окружностью и хордой заключается в том, что любую хорду можно считать как отрезок на окружности, а именно как прямую линию, соединяющую две точки на окружности. Длина хорды зависит от её положения и угла, который она образует с диаметром окружности, проходящим через её концы.
Длина хорды окружности может быть вычислена с помощью формулы:
| Аргументы | Формула |
|---|---|
| Радиус окружности (r) | Длина хорды (c) = 2 * r * sin(θ/2) |
| Угол между радиусами (θ) |
Радиус окружности можно найти, зная диаметр, который является удвоенной длиной радиуса. В то же время, угол между радиусами можно найти с помощью геометрических свойств и формул.
Таким образом, зная радиус или диаметр окружности, а также угол между радиусами, можно вычислить длину хорды окружности, используя предложенную формулу. Это позволяет решать различные задачи, связанные с окружностями и хордами в геометрии и других областях знаний.
Формула вычисления длины хорды окружности

Длина хорды окружности может быть вычислена с помощью формулы:
l = 2r * sin(θ/2)
где:
- l - длина хорды;
- r - радиус окружности;
- θ - центральный угол, соответствующий хорде.
Для вычисления длины хорды необходимо знать радиус окружности и центральный угол, который хорде соответствует. Центральный угол измеряется в радианах.
Пример:
Пусть у нас есть окружность с радиусом 5 см и центральный угол θ равен 60°. Мы можем использовать формулу для вычисления длины хорды:
l = 2 * 5 * sin(60°/2) ≈ 2 * 5 * sin(30°) ≈ 2 * 5 * 0.5 ≈ 5 см.
Таким образом, длина хорды окружности составляет 5 см. Это означает, что расстояние между любыми двумя точками на хорде составляет 5 см.
Примеры вычисления длины хорды окружности
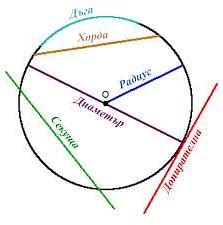
Вот несколько примеров, которые помогут вам понять, как вычислить длину хорды окружности:
Пример 1:
Дана окружность с радиусом 7 см и хорда, разделяющая окружность на две части. Найдем длину этой хорды.
Применяя формулу, длина хорды равна удвоенному произведению радиуса на синус половины центрального угла, образованного хордой.
Здесь р = 7 см и угол θ = 60° (так как половина центрального угла равна 120°).
Таким образом, длина хорды равна 2 × 7 см × sin(60°), что равно 14 см × √3 / 2 = 7 см × √3.
Таким образом, длина хорды окружности равна 7 см × √3.
Пример 2:
Предположим, что дана окружность с диаметром 10 см и хорда, разделяющая окружность на две части. Найдем длину хорды.
Радиус окружности равен половине диаметра, поэтому радиус r = 5 см.
Также, чтобы вычислить длину хорды, нам понадобится знать угол α, образованный хордой.
Длина хорды равна удвоенному произведению радиуса на синус половины центрального угла, образованного хордой. Давайте рассчитаем это.
Таким образом, длина хорды равна 2 × 5 см × sin(α/2).
В данном примере у нас нет данных о значении угла α, поэтому мы не можем рассчитать точную длину хорды. Но если было бы дано значение угла α, мы могли бы продолжить расчет, используя эту формулу.
Пример 3:
Пусть есть окружность с радиусом 9 см и хорда длиной 12 см. Найдем угол α, образованный хордой.
Мы можем использовать теорему косинусов для нахождения угла α. В этом случае, диаметр, проходящий через середину хорды, является биссектрисой этой хорды.
Тогда имеем: cos(α / 2) = (длина хорды) / (2 × радиус) = 12 см / 18 см = 2 / 3.
Используя таблицу значений или калькулятор, найдем значение угла α, равное приблизительно 48,59° (искомый угол α / 2).
Теперь, используя длину хорды и найденный угол α, можем вычислить длину хорды с помощью формулы: 2 × радиус × sin(α / 2).
Таким образом, длина хорды равна 2 × 9 см × sin(48,59°), что примерно равно 11,7 см.
Здесь мы использовали приближенное значение угла α, поэтому длина хорды также будет приближенной.
Важность знания длины хорды в геометрии и практические применения

Одним из основных применений знания длины хорды является ее использование для определения расстояния между двумя точками на окружности. Например, если нам известна длина хорды и радиус окружности, мы можем вычислить длину дуги между двумя точками, используя формулу для вычисления длины дуги окружности.
Длина хорды также используется в изучении геометрии треугольников. Например, если хорда является стороной треугольника, знание ее длины может быть полезным при вычислении площади треугольника или определении других его характеристик, таких как высоты или углы.
Практические применения знания длины хорды можно увидеть в различных областях, таких как инженерия, архитектура и дизайн. Например, в инженерии длина хорды может быть использована для расчета необходимой длины кабеля или провода, чтобы соединить две точки на окружности. В архитектуре и дизайне знание длины хорды помогает при построении и размещении декоративных элементов, таких как дуги, арки и окружности.
В-целом, знание длины хорды окружности играет важную роль в геометрии и находит применение в различных сферах жизни. Понимание этого концепта помогает решать задачи и строить точные геометрические модели.