Угол места - это угол, который образуется между линией наблюдения и горизонтальной линией. Понимание угла места и его измерение очень важно при работе с картами, навигацией и в других областях.
Если мы имеем дело с окружностью, то угол места может помочь найти длину дуги окружности между двумя точками. Важно понимать, что мы говорим не об априорном радиусе окружности, а лишь о длине дуги между двумя точками на ней.
Для вычисления длины дуги окружности по углу места используется простая формула: S = r * Φ, где S - длина дуги окружности, r - радиус окружности и Φ - угол места в радианах.
Что такое угол места?

Угол места важен при решении различных задач, связанных с навигацией и определением положения объектов. Он позволяет определить точное направление на нужное место и использовать это направление для построения планов движения или измерения расстояний.
Угол места можно измерить с помощью специальных инструментов, таких как теодолит или компас. Также существуют электронные приборы, способные измерять угол места с высокой точностью.
| Пример | Значение угла места | Описание |
|---|---|---|
| 0° | Горизонтальное направление | Наблюдаем прямо вперед |
| 90° | Вертикальное направление вверх | Наблюдаем вверх |
| 180° | Горизонтальное направление в обратную сторону | Наблюдаем назад |
| 270° | Вертикальное направление вниз | Наблюдаем вниз |
Знание угла места позволяет более точно определить местоположение объектов и использовать эту информацию в различных сферах деятельности, таких как геодезия, строительство и астрономия.
Определение и основные понятия
Угол места – это угол между прямой, соединяющей точку наблюдателя и центр окружности, и линией, соединяющей центр окружности и точку на дуге окружности.
Для определения дуги окружности по углу места необходимо знать радиус окружности и угол места. Радиус окружности – это расстояние от центра окружности до любой точки на окружности. Угол места измеряется в градусах и определяет положение точки на дуге окружности относительно наблюдателя.
Определение дуги окружности по углу места позволяет находить точку на окружности с известным углом места относительно наблюдателя. Это важное понятие в геометрии и используется в различных областях, таких как навигация, астрономия и машиностроение.
Как найти угол места?

Для нахождения угла места необходимо знать координаты точки наблюдения и точки, до которой проводится наблюдение.
Существует несколько способов вычисления угла места:
- Используя тригонометрические функции. Для этого необходимо знать высоту объекта над горизонтом и расстояние до него. Подставив эти значения в формулу, можно вычислить угол места.
- С помощью специальных инструментов, таких как угломер. Угломер позволяет определить угол места с большой точностью. Для этого необходимо измерить горизонтальный и вертикальный углы наблюдения и затем вычислить угол места с помощью формулы.
- Используя геодезические методы. Этот способ подразумевает выполнение измерений с помощью геодезических инструментов, таких как теодолит. С помощью теодолита можно измерить горизонтальный и вертикальный углы наблюдения и вычислить угол места.
Выбор метода зависит от доступных инструментов и условий наблюдения. Результаты вычислений угла места могут быть использованы в различных областях, таких как астрономия, геодезия, навигация и другие.
Методы расчета
Расчет дуги окружности по углу места может выполняться несколькими методами. В таблице ниже приведены основные методы и формулы для расчета дуги окружности.
| Метод | Формула |
|---|---|
| Метод синусов | S = R * (sin θ1 - sin θ2) |
| Метод косинусов | S = R * (cos θ2 - cos θ1) |
| Метод тангенсов | S = R * (tan θ2 - tan θ1) |
| Метод касательных | S = R * (2 * arctg((tan(θ2 - θ1) / 2)) |
Где:
S - дуга окружности
R - радиус окружности
θ1 и θ2 - углы места, заданные в радианах
Выбор метода зависит от конкретных условий задачи и доступных данных. Каждый метод имеет свои особенности и ограничения, поэтому важно правильно выбрать подходящий метод для расчета дуги окружности по углу места.
Что такое дуга окружности?
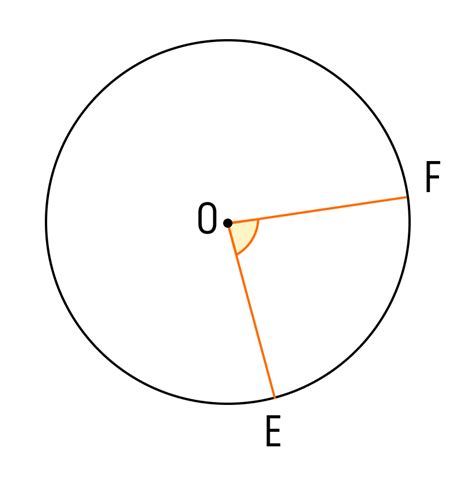
В геометрии дуга окружности играет важную роль. Она определяет длину пути, который нужно пройти, чтобы перейти из одной точки на окружности в другую. Дуга окружности также используется в различных задачах, связанных с измерением углов и расстояний.
Чтобы точнее описывать дугу окружности, используются такие понятия, как длина дуги и угол центральной части. Длина дуги определяется величиной угла, на который она открывается от центра окружности. Угол центральной части – это угол между двумя радиусами, проведенными к краям дуги. Они образуют хорду, которая является последним элементом окружности, ограниченным дугой.
Дуги окружности широко применяются в геометрии, науке и инженерии. Они помогают анализировать и решать различные задачи, связанные с геометрическими конструкциями и измерениями. Понимание и умение работать с дугами окружности – это важный элемент математического образования и практического применения геометрии.
Определение и свойства

Угол места – это угол между направлениями на два объекта от наблюдателя.
Определение дуги окружности по углу места обычно используется для нахождения расстояния между наблюдателем и объектом, а также для определения ориентации объекта относительно наблюдателя.
Для определения дуги окружности по углу места необходимо знать радиус окружности и угол места.
| Свойства | Значение |
|---|---|
| Длина дуги окружности | 2πr, где r – радиус окружности |
| Угол места | Величина от 0° до 360°, указывающая положение объекта относительно наблюдателя |
| Соотношение между длиной дуги и углом места | 1° = π/180 * r |
Зная радиус окружности и угол места, можно использовать формулу длины дуги окружности, чтобы найти длину дуги. Соотношение между длиной дуги и углом места представляет собой пропорцию, по которой можно вычислить длину дуги.