Определение дуги вписанного угла - важный элемент геометрии, который применяется в различных областях, начиная от строительства и заканчивая анализом данных. Этот метод позволяет нам рассчитать длину дуги, которую образует угол, вписанный в окружность. Открытие этой техники открывает перед нами возможности для решения различных задач, связанных с углами и окружностями.
Для определения дуги вписанного угла нам потребуются базовые знания геометрии и некоторые формулы. Окружность играет важную роль в этом процессе, поэтому основное внимание следует уделить пониманию ее свойств и структуры. В то же время, вводные сведения о тригонометрии будут полезными для расчетов и измерений.
Эта статья предлагает практическое руководство, которое поможет вам научиться определять дугу вписанного угла с помощью простых шагов и примеров. Вы узнаете, как использовать формулы и концепции геометрии для решения задач и описания окружностей. Следуя этому руководству, вы сможете углубить свои знания в области геометрии и научиться применять их на практике.
Как определить вписанный угол по дуге?

1. Найдите середину дуги, разделив ее на две равные части. Для этого можно использовать циркуль и линейку.
2. Проведите радиус из центра окружности к середине дуги. Эта линия будет являться биссектрисой вписанного угла.
3. С помощью угломера или линейки измерьте получившийся угол, который является половиной вписанного угла.
4. Умножьте измеренный угол на 2, чтобы получить значение вписанного угла.
Теперь вы знаете, как определить вписанный угол по дуге. Этот метод может быть полезен при решении геометрических задач, связанных с окружностями и углами. Удачи в обучении!
Измерение дуги: простой способ определения вписанного угла
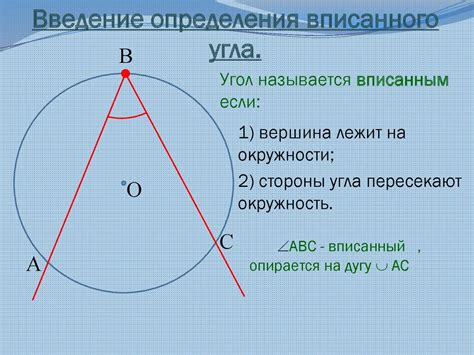
Дуга вписанного угла представляет собой часть окружности, ограниченную двумя хордами на окружности и соединяющую две точки на окружности, через которые проходят эти хорды.
Определение вписанного угла основано на измерении дуги, которую занимает этот угол на окружности. Для измерения дуги можно использовать угломерный линейк и следующие шаги:
- Выберите две точки на окружности, через которые проходят хорды, и отметьте их.
- Подключите угломерный линейк к этим точкам, приложив его к окружности.
- Зафиксируйте угол, образованный угломерным линейком, показывающим расположение двух хорд.
- Измерьте дугу, которую занимает этот угол на окружности, используя угломерный линейк как меру.
Полученное измерение дуги представляет собой значение в градусах, которое можно использовать для определения вписанного угла.
Измерение дуги является простым способом определения вписанного угла на окружности. Оно позволяет точно измерить угол, который образуется двумя хордами и проходит через две точки на окружности.
Как вычислить вписанный угол используя центральный угол?

Шаги для вычисления вписанного угла используя центральный угол:
- Найдите центр окружности.
- Проведите два радиуса, протянув их к концам дуги.
- Измерьте центральный угол между двумя радиусами, используя секундомер или универсальный угломер.
- Результат измерения центрального угла будет являться мерой вписанного угла.
Этот метод достаточно прост и позволяет легко определить меру вписанного угла. Он используется в геометрии и в различных задачах, связанных с окружностями и углами, которые образуются на их дугах. Данный способ также позволяет вычислить меру вписанного угла в тех случаях, когда нет прямых данных о самой дуге.
Применение дуг вписанного угла в геометрических расчетах

Применение дуг вписанного угла широко распространено в архитектуре, строительстве, инженерии и других отраслях. В архитектуре дуги вписанного угла позволяют определить размеры и форму арок, а также провести расчеты для создания изящных и прочных конструкций.
В строительстве дуги вписанного угла применяются для верных измерений и построения линий. Например, при проведении замеров и построении планов помещений, дуги вписанного угла используются для определения точного расположения стен, дверных и оконных проемов.
В инженерии дуги вписанного угла широко применяются для проведения расчетов при проектировании конструкций, машин и механизмов. Они позволяют определить углы наклона, размеры и общую форму элементов, а также взаимное расположение различных деталей.
Одним из наиболее удобных и практичных способов использования дуг вписанного угла является создание круглых и дуговых диаграмм. Они активно применяются в статистике, экономике, маркетинге и других областях, чтобы наглядно и наглядно представить данные и результаты анализа.
Таким образом, дуги вписанного угла являются важным инструментом в геометрических расчетах и находят широкое применение в различных отраслях. Они помогают определить размеры, форму и расположение элементов конструкций и фигур, а также наглядно представлять данные в виде диаграмм и графиков.
Таблица 1: Применение дуг вписанного угла в геометрических расчетах
| Отрасль | Применение |
|---|---|
| Архитектура | Определение размеров и формы арок |
| Строительство | Измерение и построение линий |
| Инженерия | Проектирование конструкций и механизмов |
| Статистика и экономика | Представление данных в диаграммах |
Вычисление координат дуги вписанного угла в пространстве
Для начала, необходимо определить точки начала и конца дуги окружности. Для этого используется формула:
X1 = Xc + R * cos(α/2)
Y1 = Yc + R * sin(α/2)
X2 = Xc + R * cos(α)
Y2 = Yc + R * sin(α)
Эти формулы позволяют вычислить координаты точек начала и конца дуги окружности. Здесь X1 и Y1 представляют собой координаты начальной точки, а X2 и Y2 - координаты конечной точки.
Чтобы получить координаты дуги, можно воспользоваться дугой окружности и формулой Брезенхэма. Данная формула позволяет аппроксимировать дугу окружности с помощью отдельных точек, заданных координатами.
В общем виде, для каждой точки на дуге окружности нужно вычислить ее координаты. Для этого можно использовать формулы:
X = Xc + R * cos(t)
Y = Yc + R * sin(t)
Здесь X и Y - это координаты точки на дуге окружности, t - это параметр, охватывающий всю дугу с абсолютными значениями от 0 до α.
С помощью данных формул, можно вычислить координаты точек на дуге вписанного угла в пространстве. Эти координаты могут быть использованы в различных задачах геометрии или программирования.
Использование дуг вписанного угла в архитектуре и дизайне

Дуги вписанного угла представляют собой важный элемент в архитектуре и дизайне, который использовался на протяжении многих веков. Они придают структурам и объектам эстетическую привлекательность и позволяют создать уникальные визуальные эффекты.
В архитектуре, дуги вписанного угла часто используются для создания арочных окон, дверных проемов и арок. Они добавляют изящество и элегантность внешнему виду зданий, делая их более привлекательными и уникальными. Дуги вписанного угла могут быть разных размеров и форм, от круглых до остроугольных, что позволяет архитекторам создавать разнообразные дизайнерские решения.
В дизайне интерьера, дуги вписанного угла также играют важную роль. Они могут быть использованы для создания изгибов и изгибчивых линий в мебели, освещении и декоративных элементах, добавляя грацию и движение в пространство. Дуги вписанного угла могут быть использованы как самостоятельный элемент или в сочетании с другими геометрическими формами, например, с прямыми или кривыми линиями.
В дизайне ландшафта, дуги вписанного угла могут использоваться для создания декоративных элементов, таких как арки или рамы для цветочных клумб. Они помогают придать участку гармонию и симметрию, а также создать архитектурные эффекты на открытом пространстве.
Использование дуг вписанного угла в архитектуре и дизайне предоставляет дизайнеру безграничные возможности для творчества. Они могут быть использованы как основной декоративный элемент или в качестве дополнительного акцента, добавляя интерес и уникальность в окружающую среду.
Таким образом, дуги вписанного угла являются важным инструментом для создания эстетически привлекательных и функциональных архитектурных и дизайнерских решений. Они добавляют изящество и характер в различные структуры и объекты, придавая им уникальность и привлекательность.
Как создать эффект дуги вписанного угла на веб-странице

Создание эффекта дуги вписанного угла на веб-странице может быть интересным и креативным способом украшения вашего сайта. Этот эффект может быть использован для добавления визуального интереса к различным элементам интерфейса, таким как заголовки, меню или кнопки.
Для создания эффекта дуги вписанного угла на веб-странице можно использовать CSS-свойство border-radius. Это свойство позволяет задать радиус закругления углов элементов. Чтобы создать эффект дуги вписанного угла, достаточно задать значение 50% для свойства border-radius у нужного элемента. Например:
<div style="width: 200px; height: 200px; background-color: #ccc; border-radius: 50%;"></div>
Этот код создаст круглый элемент размером 200x200 пикселей с серым фоном.
Однако, чтобы создать эффект дуги вписанного угла, нужно включить в элемент еще один блок с фоном, которые будет являться дугой. С помощью CSS-свойства transform можно повернуть этот блок и сделать так, чтобы дуга выглядела именно так, как требуется. Например:
<div style="position: relative; width: 200px; height: 200px; background-color: #ccc; border-radius: 50%;">
<div style="position: absolute; top: 50%; left: 50%; width: 200px; height: 200px; background-color: #f00; transform: rotate(45deg);"></div>
</div> В данном примере создается круглый элемент со слегка красной дугой на правом верхнем углу элемента. С помощью свойств top: 50% и left: 50% мы поместили блок с дугой в центр круга, а с помощью свойства transform: rotate(45deg) повернули его на 45 градусов.
Теперь вы можете экспериментировать с различными значениями радиуса, цветом и поворотом дуги, чтобы создать нужный вам эффект вписанного угла на веб-странице.
Примеры использования дуг вписанного угла в различных задачах

| Пример задачи | Решение |
|---|---|
| 1. Найти значение вписанного угла, если известны длины дуг, пересекаемых этим углом. | Пользуясь свойством вписанного угла, можно установить соответствие между дугами и углом. Затем используя формулы для длины дуги и радиуса окружности, можно найти значение угла. |
| 2. Найти длину дуги окружности, если известен угол, на который эта дуга накрывает центральный угол. | Пользуясь свойством центрального и вписанного угла, можно установить соответствие между углом и дугой. Затем используя формулу для нахождения длины дуги, можно найти её значение. |
| 3. Доказать, что две дуги равны, используя свойство вписанного угла. | Предположим, что две дуги равны и построим соответствующий вписанный угол. Затем используя свойства этого угла и критерий равенства дуг, можно доказать, что дуги действительно равны. |
Это лишь некоторые примеры использования дуг вписанного угла в различных задачах на геометрию. Понимание данных концепций и умение применять их в практических задачах является важным навыком для успешного решения подобных задач.