Тангенс - это тригонометрическая функция, которая определяется как отношение противолежащего катета к прилежащему катету прямоугольного треугольника. Градусная мера тангенса - это угол, для которого данный тангенс принимает определенное значение. Если вы хотите узнать, как найти градусную меру тангенса, вы находитесь в правильном месте.
Первым шагом в нахождении градусной меры тангенса является получение значения тангенса. Для этого необходимо определить противолежащий и прилежащий катеты и использовать соответствующую формулу. После этого можно перейти к определению градусной меры тангенса.
Один из способов нахождения градусной меры тангенса - использование тригонометрических таблиц или калькулятора. В таких таблицах приведены значения тангенса для различных углов. Вы можете найти значение тангенса, которое соответствует вашей изначальной задаче, и определить градусную меру для этого значения.
Еще один способ нахождения градусной меры тангенса - использование обратных функций тригонометрии. Например, если вам изначально известно значение тангенса, вы можете использовать обратную функцию тангенса (арктангенс) для определения градусной меры этого значения. Это особенно полезно, если вы хотите найти градусную меру тангенса именно для заданного значения, а не для значения из таблицы.
Что такое градусная мера тангенса?
Градусная мера тангенса обозначается как tg угла и измеряется в градусах. Для нахождения градусной меры тангенса может использоваться таблица значений или математическая формула. Часто она используется для вычисления угла при известных значениях противоположного и прилегающего катетов.
Пользуясь градусной мерой тангенса, можно решать множество геометрических и физических задач. Она широко применяется в таких областях, как астрономия, строительство, навигация, а также при решении задач связанных с оптикой, электричеством и магнетизмом.
Важно помнить, что градусная мера тангенса имеет свои ограничения и нельзя применять ее повсеместно. Например, в вычислениях, требующих высокой точности, часто используется радианная мера тангенса.
Математические основы

Градус – это единица измерения плоского угла, обозначаемая символом °. Полный угол составляет 360 градусов, при этом каждый градус может быть разделен на 60 минут, а каждая минута может быть разделена на 60 секунд. Для удобства использования, градусы могут быть представлены в десятичной форме, например, 30.5 градусов.
Тангенс угла – это отношение противолежащего катета к прилежащему катету прямоугольного треугольника. Он часто обозначается сокращенно как tan или tg. Для вычисления точного значения тангенса угла, необходимо знать все стороны треугольника или иметь информацию об отношении сторон.
Однако, чаще всего значение градусной меры тангенса вычисляется с использованием таблиц и графиков или с помощью калькулятора, который имеет встроенную функцию для расчета тангенса. В настоящее время существует также множество онлайн-инструментов и приложений, которые могут помочь в рассчетах.
| Угол (в градусах) | Тангенс |
|---|---|
| 0 | 0 |
| 30 | 0.577 |
| 45 | 1 |
| 60 | 1.732 |
| 90 | неопределен |
В таблице приведены некоторые расчеты градусной меры тангенса для некоторых углов. Заметим, что при угле 90 градусов тангенс является неопределенным, так как в этом случае прилежащий катет равен нулю, а противолежащий катет несуществующий.
Простейший способ поиска градусной меры тангенса

Для нахождения градусной меры тангенса необходимо выполнить следующие шаги:
- Выберите значение угла в радианах, для которого вы хотите найти тангенс.
- Воспользуйтесь калькулятором для вычисления значения тангенса данного угла.
- Полученный результат представит собой численное значение тангенса данного угла.
Если вы предпочитаете использовать таблицу значений тангенса, то можно воспользоваться следующей таблицей:
| Угол (в градусах) | Тангенс |
|---|---|
| 0 | 0 |
| 30 | 0.577 |
| 45 | 1 |
| 60 | 1.732 |
| 90 | бесконечность |
Обратите внимание, что для углов 0, 90 и их кратных значений тангенс не определен.
Подробная формула для определения градусной меры тангенса

Для определения градусной меры тангенса необходимо знать значение противоположной стороны (a) и значение прилежащей стороны (b) в прямоугольном треугольнике. Формула для расчета градусной меры тангенса выглядит следующим образом:
| Тангенс угла (Т) = | a | / | b |
Таким образом, чтобы получить градусную меру тангенса, необходимо разделить значение противоположной стороны на значение прилежащей стороны треугольника.
Пример:
Пусть в прямоугольном треугольнике противоположная сторона (a) равна 5, прилежащая сторона (b) равна 3. Чтобы найти градусную меру тангенса (Т), необходимо разделить 5 на 3:
| Тангенс угла (Т) = | 5 | / | 3 | = | 1.6667 |
Таким образом, градусная мера тангенса угла в треугольнике равна 1.6667.
Практическое применение

Тангенс:
Градусная мера тангенса находит свое применение в различных областях науки и техники. Например, в геометрии тангенс используется для решения треугольников, нахождения углов и расчета длин сторон. Также тангенс применяется в физике при изучении колебаний и волн, а также в радиоэлектронике при расчете параметров антенн.
Однако наиболее распространенное практическое применение тангенса можно найти в области технических наук, связанных с инженерией и строительством. Например, тангенс используется для расчета наклона поверхностей и склонов при проектировании дорог и железных дорог, строительстве зданий, мостов и туннелей.
Пример:
Представим ситуацию, когда строительные инженеры планируют построить мост через реку. Для того чтобы точно определить угол наклона железнодорожной подъездной площадки к мосту, инженерам необходимо знать градусную меру тангенса данного угла. С помощью этой величины инженеры смогут правильно рассчитать длину и высоту подъездной площадки, чтобы обеспечить безопасное движение по ней.
Таким образом, градусная мера тангенса имеет огромное практическое применение в различных областях, где требуется точный расчет углов, наклонов и длин.
Как применять градусную меру тангенса в реальной жизни?
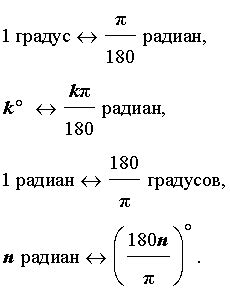
- Инженерные расчеты: Градусная мера тангенса используется инженерами при проектировании различных строительных объектов, таких как мосты, здания и дороги. Она позволяет определить угол наклона отдельных элементов конструкции и выбрать правильную геометрию для обеспечения их прочности.
- Навигация: При использовании карт и навигационных приборов, градусная мера тангенса позволяет определить угол между двумя направлениями и помочь в построении наиболее эффективного маршрута.
- Астрономия: Градусная мера тангенса используется астрономами для изучения движения небесных тел. Она позволяет измерять угол наклона планет и звезд, а также определить их положение на небосводе.
- Физика: В физике, угол наклона плоскости может быть измерен с помощью градусной меры тангенса. Это позволяет определить силу трения и провести различные эксперименты связанные с наклонными плоскостями.
Примеры решений
Пример 1:
Найдем градусную меру тангенса для угла α в прямоугольном треугольнике ABC. Угол α противолежит стороне AC.
Известно, что сторона AB равна 5 см, а сторона BC равна 3 см.
Для начала, найдем значение тангенса угла α:
тангенс угла α = противоположная сторона / прилежащая сторона
тангенс α = BC / AB
тангенс α = 3 / 5
Рассчитаем численное значение тангенса:
тангенс α ≈ 0.6
Чтобы найти градусную меру тангенса, воспользуемся обратной функцией тангенса - арктангенсом (или tan-1).
градусная мера α = arctan(тангенс α)
градусная мера α ≈ arctan(0.6)
С помощью калькулятора или математического программного обеспечения можно рассчитать приближенное значение градусной меры тангенса:
градусная мера α ≈ 30.96°
Пример 2:
Рассмотрим еще один пример с прямоугольным треугольником ABC. В данном случае известны сторона AB = 8 см и угол α равен 45°.
Сначала нужно найти значение тангенса угла α:
тангенс α = противоположная сторона / прилежащая сторона
тангенс α = AC / BC
Находим противоположную катету с помощью теоремы Пифагора:
AC2 = AB2 - BC2
AC2 = 82 - BC2
AC2 = 64 - BC2
AC2 = 8 - BC2
AC ≈ √(8 - BC2)
С учетом угла α = 45°, получаем:
тангенс α = (√(8 - BC2)) / BC
Решая эту уравнение численно или с помощью математического программного обеспечения, найдем:
тангенс α ≈ 0.4142
Затем, с применением обратной функции тангенса:
градусная мера α = arctan(тангенс α)
градусная мера α = arctan(0.4142)
Используя калькулятор или компьютерную программу для математических расчетов, найдем градусную меру тангенса:
градусная мера α ≈ 22.5°
Примеры поиска градусной меры тангенса

Для нахождения градусной меры тангенса можно использовать как тригонометрический круг, так и математические формулы. Вот несколько примеров:
Пример 1:
Пусть угол А составляет 45 градусов. Тогда градусная мера тангенса этого угла будет равна:
тан А = sin А / cos А
тан 45° = sin 45° / cos 45°
тан 45° = 1 / 1 = 1
Таким образом, градусная мера тангенса угла 45° равна 1.
Пример 2:
Пусть угол В составляет 30 градусов. Для нахождения градусной меры тангенса этого угла мы можем воспользоваться таблицей значений тригонометрических функций:
тан В = sin В / cos В
Значение синуса и косинуса для 30° можно найти в таблице:
sin 30° = 0.5
cos 30° = √3 / 2 ≈ 0.866
Тогда градусная мера тангенса угла 30° будет:
тан 30° = 0.5 / 0.866 ≈ 0.577
Таким образом, градусная мера тангенса угла 30° приближенно равна 0.577.
Пример 3:
Пусть угол С составляет 60 градусов. Для нахождения градусной меры тангенса этого угла мы также можем воспользоваться таблицей значений тригонометрических функций:
тан С = sin С / cos С
Значение синуса и косинуса для 60° можно найти в таблице:
sin 60° = √3 / 2 ≈ 0.866
cos 60° = 0.5
Тогда градусная мера тангенса угла 60° будет:
тан 60° = 0.866 / 0.5 ≈ 1.732
Таким образом, градусная мера тангенса угла 60° приближенно равна 1.732.