Изучение закона всемирного тяготения является важной частью физики. Один из ключевых параметров в этом законе - масса. Но как находить массу с помощью формулы и какие методы расчета применять?
Согласно закону всемирного тяготения, сила притяжения между двумя телами прямо пропорциональна их массам, а обратно пропорциональна квадрату расстояния между ними. Зная эту формулу, можно определить массу объекта, если известны другие параметры.
Существует несколько методов расчета массы из закона всемирного тяготения. Один из них - метод, основанный на измерении силы притяжения между объектами с известными массами. Измерив силу, можно выразить массу искомого объекта через известные массы и расстояние между ними.
Еще один метод - определение массы путем измерения времени свободного падения объекта под действием гравитационной силы. Положив время и расстояние в формулу, можно найти массу объекта.
Закон всемирного тяготения
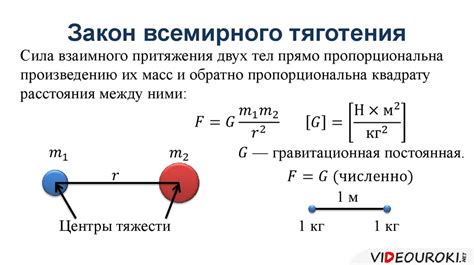
Согласно закону всемирного тяготения, сила притяжения между двумя объектами прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними. Математически этот закон выражается формулой:
F = G * (m1 * m2) / r^2
Где F - сила притяжения между объектами, G - гравитационная постоянная, m1 и m2 - массы объектов, а r - расстояние между ними.
Закон всемирного тяготения позволяет рассчитывать силу притяжения и массу объекта при известной силе притяжения и расстоянии до него. Для этого формулу можно преобразовать и выразить массу одного из объектов:
m1 = (F * r^2) / (G * m2)
Таким образом, с помощью закона всемирного тяготения можно определить массу объекта, если известна сила притяжения между ними и расстояние.
Использование данного закона широко распространено в физике и астрономии для изучения движения небесных тел, планет, спутников и других объектов в космосе. Он также лежит в основе работы спутниковых систем и космических миссий.
Первые шаги в расчете массы

Чтобы рассчитать массу, необходимо знать два параметра: силу гравитационного притяжения и ускорение свободного падения. Для начала определимся с физическими величинами и единицами измерения, которые мы будем использовать в расчетах.
Сила гравитационного притяжения обозначается символом F и измеряется в ньютонах (Н). По закону всемирного тяготения, ее значение определяется формулой:
F = G * (m1 * m2) / r^2
где G - гравитационная постоянная (6,67430 × 10^(-11) Н·м^2/кг^2), m1 и m2 - массы двух взаимодействующих тел, r - расстояние между их центрами.
Ускорение свободного падения обозначается символом g и измеряется в метрах в секунду в квадрате (м/с²). Для поверхности Земли его значением принято считать приближенно равным 9,8 м/с².
С помощью этих данных и формулы мы сможем рассчитать массу тела. Для этого необходимо известно значение силы гравитационного притяжения и ускорения свободного падения, а также значение расстояния между телами.
Обратите внимание, что расчет массы по данной формуле возможен только при условии, что у нас уже есть информация о силе гравитационного притяжения и ускорении свободного падения. В противном случае, требуется провести дополнительные измерения или получить данные из других источников.
Опыты Эйнштейна и масса

Один из самых известных ученых XX века, Альберт Эйнштейн, сыграл ключевую роль в развитии теории относительности. В своих опытах он исследовал различные аспекты массы и доказал основные законы, которые сейчас используются для рассчета массы.
Эйнштейн пояснил, что масса тела определяется его энергией по знаменитой формуле E=mc², где E - энергия, m - масса, c - скорость света. Эта формула указывает на то, что энергия и масса являются взаимосвязанными и взаимодополняющими понятиями.
Для определения массы тела, базируясь на законе всемирного тяготения, Эйнштейн также разработал ряд методов. Он использовал различные устройства и датчики для измерения силы притяжения и определения массы. Эти опыты дали основу для разработки современных методов расчета массы.
Опыты Эйнштейна оказали огромное влияние на наше понимание массы и ее взаимосвязи с энергией. Его открытия и исследования легли в основу современной физики и имеют неоценимое значение для науки в целом.
Планетарные весы и методы измерения массы

Для измерения массы планеты с помощью планетарных весов используются несколько методов. Один из них - метод измерения времени свободного падения. Суть метода заключается в определении времени, за которое предмет свободно падает на поверхности планеты. По правилам классической механики, время свободного падения зависит от массы планеты и силы тяжести. Путем измерения времени свободного падения и зная силу тяжести, можно рассчитать массу планеты.
Еще один метод измерения массы планеты - метод измерения радиуса орбиты спутника. Этот метод основывается на третьем законе Кеплера, который связывает период обращения спутника вокруг планеты с массой планеты и радиусом его орбиты. Зная период обращения спутника и радиус его орбиты, можно рассчитать массу планеты.
Также существуют другие методы измерения массы планеты, такие как измерение деформации поверхности планеты под воздействием ее собственной гравитации или использование спутниковых данных для расчета гравитационного поля.
Планетарные весы и методы измерения массы планеты являются важными инструментами для астрономии и космических исследований. Они позволяют узнать массу планеты и лучше понять ее структуру и эволюцию.
Гравитационная формула Ньютона и расчет массы
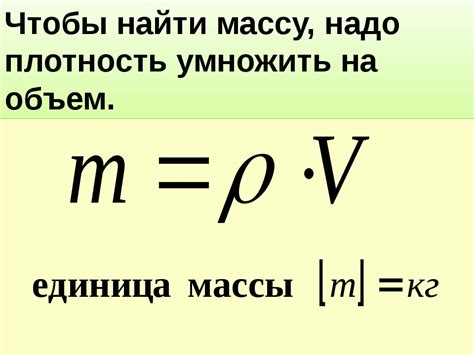
Математически, гравитационная формула Ньютона записывается как:
где - сила притяжения между телами,
- гравитационная постоянная,
и
- массы тел,
- расстояние между телами.
Расчет массы тела на основе гравитационной формулы Ньютона может быть произведен, если известны значения силы притяжения, гравитационной постоянной и расстояния между телами. При этом формула может быть переставлена для получения значения массы одного из тел:
Гравитационная формула Ньютона и методы ее использования являются важными инструментами в различных областях физики и астрономии, позволяющими определять массу тел на основе данных об их взаимодействии.
| Символ | Название | Значение | Единица измерения |
|---|---|---|---|
| G | Гравитационная постоянная | 6,67430 × 10-11 | м3⋅кг-1⋅с-2 |
| m1 | Масса тела 1 | кг | |
| m2 | Масса тела 2 | кг | |
| F | Сила притяжения | Н | |
| r | Расстояние между телами | м |
Расчет массы с использованием ускорения свободного падения

Для расчета массы тела с использованием ускорения свободного падения необходимо знать два параметра: ускорение свободного падения g и сила тяготения F.
Формула для расчета массы выглядит следующим образом:
m = F / g
Где:
m - масса тела,
F - сила тяготения,
g - ускорение свободного падения.
Для точных расчетов необходимо использовать значения ускорения свободного падения, принятые в научных и инженерных расчетах. Для Земли значение ускорения свободного падения примерно равно 9,81 м/с².
Таким образом, для расчета массы тела с использованием ускорения свободного падения необходимо знать силу тяготения и значение ускорения свободного падения на данной планете или спутнике.
Формула расчета массы на основе движения орбиты спутника
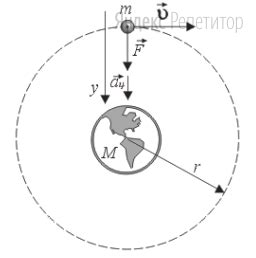
Расчет массы объекта, например планеты или звезды, может быть выполнен на основе движения орбиты спутника вокруг данного объекта. Этот метод расчета впервые был предложен Исааком Ньютоном и стал основой для развития классической механики.
Формула, позволяющая определить массу объекта, основывается на известной формуле закона всемирного тяготения:
F = G * (m1 * m2) / r^2
где:
F - сила притяжения между двумя объектами,
G - гравитационная постоянная (6,67430 * 10^-11 м^3 кг^-1 с^-2),
m1 и m2 - массы двух объектов (объект, который движется вокруг и объект, вокруг которого движется спутник),
r - расстояние между центрами двух объектов.
На практике мы можем использовать эту формулу для определения массы планеты, например, путем наблюдения орбиты спутника, который находится на заданной высоте над поверхностью планеты.
Используя известные значения гравитационной постоянной и радиуса орбиты спутника, мы можем записать формулу следующим образом:
F = G * (m1 * m2) / r^2
G * m2 = F * r^2 / m1
m2 = (F * r^2) / (G * m1)
Где m2 - масса планеты или объекта, вокруг которого движется спутник.
Таким образом, путем измерения силы, необходимой для поддержания спутника на заданной орбите, и известной массы спутника и поверхности планеты, мы можем определить массу объекта с помощью данной формулы.