Функция арксинуса (или обратная синусоида) - это элементарная функция, обратная к синусу. В математике она обозначается символом asin(x) или arcsin(x). Она позволяет находить такой угол, синус которого равен заданному числу.
Однако, при работе с этой функцией необходимо помнить о ее области определения, чтобы избежать ошибок. Область определения функции арксинуса включает в себя все значения, для которых арксинус имеет смысл. Так как мы говорим о значении синуса, то значения арксинуса ограничены диапазоном от -1 до 1.
То есть, область определения функции арксинуса выглядит следующим образом: D = [-1, 1]. На этом интервале арксинус является строго возрастающей функцией. Значит, для любого значения из этого диапазона мы можем найти единственное значение арксинуса.
Однако стоит учесть, что арксинус не определен для значений, выходящих за пределы этого интервала. Например, арксинус от 1.5 не имеет смысла и не может быть вычислен. Поэтому, при использовании функций, включающих в себя арксинус, всегда стоит проверять, находится ли значение в пределах области определения.
Как найти область определения функции арксинуса

Область определения функции арксинуса (sin-1(x)) определяется ограничениями на аргумент x, для которых функция арксинуса имеет математический смысл. Функция арксинуса обратна к функции синуса, поэтому ее значения ограничены значениями функции синуса.
Зная, что аргумент синуса должен принадлежать отрезку [-1, 1], можно определить область определения арксинуса как множество значений x, для которых выполнено неравенство -1 ≤ x ≤ 1.
Таким образом, область определения функции арксинуса состоит из всех действительных чисел x, таких что -1 ≤ x ≤ 1.
| Функция | Область определения |
|---|---|
| sin-1(x) | -1 ≤ x ≤ 1 |
Обратите внимание, что для аргументов вне этого интервала, функция арксинуса не имеет значения и не определена.
Научитесь распознавать арксинус
Функция арксинус определена только для значений от -1 до 1. Если мы попытаемся взять арксинус от числа за пределами этого интервала, получим неопределенность.
Область определения функции арксинус задается следующим образом:
Dom(arcsin(x)) = [-1, 1]
Таким образом, если аргумент функции арксинус находится в указанном интервале, функция определена и имеет ровно одно значение.
Понимание области определения функции арксинуса важно при решении уравнений и неравенств, а также при проведении анализа графика этой функции. Знание этой информации поможет вам избегать ошибок и выходить на правильные решения.
Узнайте, что такое область определения

Функция арксинуса, обозначаемая как arcsin(x) или sin-1(x), является обратной функцией для синуса. Она позволяет находить угол, для которого синус равен указанному значению. Например, если мы знаем, что sin(x) = 1/2, то функция арксинуса может помочь нам определить, что x = π/6.
Однако, не все значения x подходят для функции арксинуса. Функция арксинуса определена только для значений, которые лежат в диапазоне от -1 до 1 включительно. Это означает, что область определения функции арксинуса равна [-1, 1].
Если мы попытаемся вычислить арксинус для значения x, которое не принадлежит к этому диапазону, мы получим неопределенность или ошибку. Например, арксинус от 2 или -3 не существует.
Область определения функции арксинуса можно представить в виде таблицы:
| x | Область определения |
|---|---|
| -1 ≤ x ≤ 1 | [-1, 1] |
Из этой таблицы видно, что функция арксинуса определена только для значений x, которые лежат в диапазоне от -1 до 1 включительно.
Понятие обратной функции
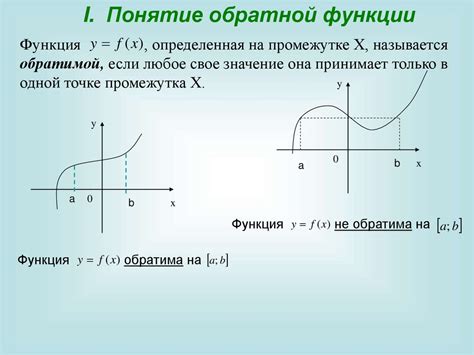
Другими словами, если у нас есть функция f(x), то обратная функция к ней, обозначается как f-1(y), может преобразовывать значения y обратно в значения x.
Для того, чтобы функция имела обратную функцию, она должна обладать некоторыми свойствами. Во-первых, каждому x из области определения функции должен соответствовать только один y. Во-вторых, каждому y из области значений функции должен соответствовать только один x. Если эти условия выполняются, то функция считается обратимой и имеет обратную функцию.
Обратная функция f-1(y) может использоваться для решения уравнений, в которых искомое значение является аргументом функции f(x). Также она может применяться для нахождения значения x по заданному значению y.
Ограничения функции арксинуса
Одной из основных особенностей функции арксинуса является то, что она определена только в определенном диапазоне значений, который ограничен интервалом [-1, 1]. Это означает, что функция арксинуса может принимать только значения от -π/2 до π/2 включительно. Если аргумент функции выходит за пределы этого интервала, то функция арксинуса не будет определена.
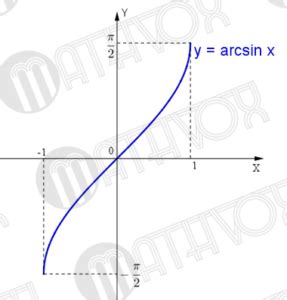
Этот интервал [-1, 1] соответствует области, в которой синусная функция принимает значения от -1 до 1. Функция арксинуса возвращает угол, значение синуса которого равно данному аргументу.
Еще одно ограничение функции арксинуса связано с ее графиком. График функции арксинуса - это часть графика синусной функции, ограниченная интервалом [-π/2, π/2] по оси абсцисс и [-π/2, π/2] по оси ординат.
Зная эти ограничения и определение функции арксинуса, можно грамотно использовать эту функцию для решения различных задач, связанных с тригонометрией, геометрией и прочими областями математики.
Допустимое множество значений

При этом, для функции арксинуса область определения ограничена диапазоном от -π/2 до π/2 (математически записывается как -π/2 ≤ x ≤ π/2), где x это аргумент функции арксинуса. Это означает, что функция арксинуса принимает значения только в этом интервале и не может быть определена за его пределами.
Допустимое множество значений функции арксинуса является действительными числами из интервала от -π/2 до π/2 включительно.
Границы области определения

Область определения функции арксинуса ограничена значениями, которые может принимать ее аргумент. Аргумент арксинуса должен принадлежать интервалу от -1 до 1 включительно, чтобы функция была определена.
Границы области определения обусловлены свойствами синусной функции, которой является аргумент арксинуса. Синусная функция принимает значения от -1 до 1 включительно. Арксинус является обратной функцией синусу, поэтому его аргумент должен быть ограничен теми же значениями.
Если аргумент арксинуса выходит за пределы области определения, то функция не имеет значения и является неопределенной. Границы области определения можно записать следующим образом: DARCSIN = [-1, 1].
Важно помнить, что область определения арксинуса ограничена значениями аргумента, а не значениями самой функции. Арксинус может принимать любое значение в интервале от -π/2 до π/2 радиан включительно.