Радиус окружности – одно из основных понятий в физике, которое используется для определения формы и размеров объектов. Понимание радиуса окружности является важным шагом в обучении физике и может иметь практическое применение во многих областях, включая геометрию, астрономию и инженерию.
Радиус окружности определяется как расстояние от центра окружности до любой точки на ее границе. Обозначается буквой "r", радиус является половиной диаметра окружности. Радиус окружности является ключевым параметром, который позволяет определить ее площадь, длину окружности и многое другое.
Если вам нужно определить радиус окружности, вам понадобятся соответствующие формулы. Для начала, если у вас есть диаметр окружности, радиус можно найти по формуле r = d/2, где d - диаметр. А если известна площадь окружности, радиус можно вычислить по формуле r = √(S/π), где S - площадь.
Понимание радиуса окружности ценно при работе с геометрическими фигурами, такими как круги, и при решении задач в физике. Этот параметр помогает определить спектр свойств и характеристик окружности, что открывает дверь для дальнейшего изучения и практического применения данного понятия.
Законы физики и определение радиуса окружности

Один из самых важных законов, связанных с радиусом окружности, - закон Гука. Он устанавливает связь между силой и деформацией упругого материала. При растяжении или сжатии упругого материала, радиус окружности может измениться. Формула Гука позволяет определить изменение радиуса окружности в зависимости от силы, деформации и характеристик материала.
Еще одним важным физическим законом, который связан с радиусом окружности, является закон всемирного тяготения Ньютона. Он говорит о том, что все тела притягиваются друг к другу силой, пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними. В этом законе радиус окружности определяет расстояние между центрами притягивающихся тел.
Также, при изучении движения тел и определении радиуса окружности играют важную роль законы Ньютона о движении. Эти законы определяют движение тела в пространстве и связывают силу, массу и ускорение тела. В формулах, описывающих движение, радиус окружности может присутствовать как параметр орбитальной траектории тела.
Таким образом, знание физических законов и умение использовать соответствующие формулы позволяют определить радиус окружности в разных физических задачах. От расстояния между точками центра и окружности, изменения формы окружности до орбитальной траектории в пространстве - радиус окружности играет важную роль в понимании физического мира.
Радиус окружности: понятие и применение
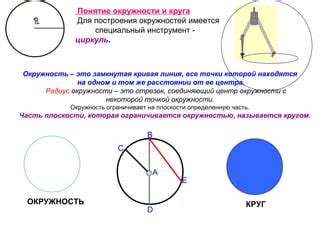
Радиус окружности имеет множество применений в физике. В механике, например, он используется для определения скорости вращения твердого тела, такого как колесо автомобиля. Радиус окружности является элементом формулы для вычисления линейной скорости вращения тела, где он связан с угловой скоростью и длиной дуги, пройденной телом.
Кроме того, в электричестве и магнетизме радиус окружности используется для описания траектории, по которой движется заряженная частица в магнитном поле. Известный величина радиуса, масса частицы и интенсивность магнитного поля позволяют определить радиус окружности, по которой будет двигаться частица.
Радиус окружности также находит применение в оптике, где он используется для определения фокусного расстояния линзы. В этом случае радиус окружности связан с кривизной поверхности линзы и позволяет определить ее оптические свойства, такие как фокусное расстояние и фокусное число.
Связь радиуса окружности с другими физическими величинами
Величина радиуса окружности обозначается символом R. Она может быть применена во множестве физических задач, и знание ее значения позволяет нам анализировать и предсказывать значения других физических величин.
Одним из простых примеров связи радиуса окружности с другими физическими величинами является длина окружности. Формула для вычисления длины окружности - это 2πR, где π - это число пи, примерное значение которого равно 3,14. Таким образом, мы можем найти длину окружности, если мы знаем значение радиуса.
Площадь круга также имеет прямую зависимость от радиуса окружности. Формула для вычисления площади круга = πR^2. В этих выражениях можно заметить, что радиус возводится в квадрат. Это означает, что даже небольшое изменение радиуса окружности может значительно изменить его площадь.
Радиус окружности также играет важную роль в изучении кинематики и динамики. Например, скорость, с которой тело движется по окружности, зависит от радиуса и времени, прошедшего во время вращения. Формула для вычисления такой скорости - это V = 2πR/T, где V - скорость, T - время.
Таким образом, радиус окружности является основным параметром, который устанавливает связь между окружностью и другими физическими величинами. Понимая эту связь, мы можем применять различные формулы для получения информации о радиусе, длине окружности, площади круга и скорости вращения объектов.
Формулы расчета радиуса окружности в разных сферах физики
В физике существует несколько сфер, в которых необходимо определить радиус окружности. Рассмотрим некоторые из них:
| Сфера физики | Формула для расчета радиуса окружности |
|---|---|
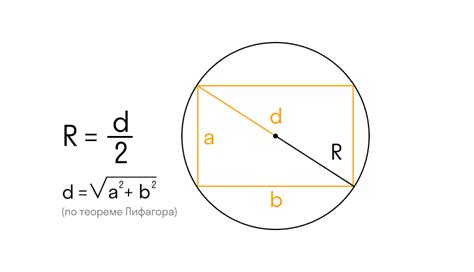
| Геометрия | Радиус окружности - это расстояние от центра окружности до любой точки на ее окружности. Формула для расчета радиуса окружности в геометрии: r = d/2, где d - диаметр окружности. |
| Электричество и магнетизм | Радиус окружности, по которой двигается электрический заряд в магнитном поле, можно определить с помощью формулы r = mv/qB, где m - масса заряда, v - скорость его движения, q - величина заряда, B - магнитная напряженность. |
| Механика | В механике радиус окружности может быть определен с помощью формулы r = v^2 / (a * sinθ), где v - скорость объекта, a - центростремительное ускорение, θ - угол между направлением движения объекта и радиусом окружности. |
| Оптика | В оптике радиус окружности может быть определен с помощью формулы r = f/2, где f - фокусное расстояние линзы. |
| Квантовая механика | В квантовой механике радиус окружности может быть определен с помощью формулы r = n²ħ² / (mke²), где n - главное квантовое число, ħ - постоянная Планка, m - масса электрона, ke - электростатическая постоянная. |
Учитывайте, что в каждой конкретной ситуации расчет радиуса окружности может требовать использования других параметров и формул. Важно учесть контекст и задачу, с которой вы сталкиваетесь. Знание соответствующих формул и их применение помогут вам правильно определить радиус окружности в различных сферах физики.
Практическое использование радиуса окружности в физике

Один из примеров практического использования радиуса окружности может быть в области механики. Например, при изучении движения тела по окружности, радиус окружности играет важную роль в определении скорости и ускорения тела. Формула для определения радиуса окружности в данном случае будет зависеть от известных величин, таких как период движения и линейная скорость.
Радиус окружности также используется в оптике. Например, в определении радиуса кривизны сферической поверхности линзы, который позволяет определить ее фокусное расстояние. Значение радиуса окружности в данном случае будет влиять на фокусное расстояние и позволит определить свойства линзы и возможности ее использования.
Кроме того, радиус окружности применяется в электромагнетизме. Например, в законе Кулона для определения силы взаимодействия между двумя точечными зарядами, радиус окружности является расстоянием между ними. Знание радиуса позволяет определить силу и направление электростатического взаимодействия между зарядами.
Практическое использование радиуса окружности в физике позволяет анализировать и предсказывать различные явления и свойства объектов и систем. Корректное определение и учет радиуса окружности является важным шагом при решении физических задач и проведении экспериментов.