Окружность является одной из важнейших геометрических фигур, которая окружает нас повсюду. Она представляет собой множество точек, равноудаленных от одной фиксированной точки, называемой центром окружности. Важным параметром окружности является ее радиус, который определяет ее размер. Но что делать, если нам известна площадь кругового сектора, а требуется найти радиус окружности? В этой статье мы рассмотрим формулу для вычисления радиуса окружности по площади кругового сектора и приведем несколько примеров вычислений.
Формула для вычисления радиуса окружности по площади кругового сектора очень проста и основана на базовых математических принципах. Она позволяет найти радиус окружности, используя известную площадь кругового сектора и угол, под которым он занимает центральную часть окружности. Формула имеет следующий вид:
Радиус = квадратный корень ( (Площадь * 360) / (π * Угол) )
Где:
- Радиус - радиус окружности;
- Площадь - площадь кругового сектора;
- Угол - угол, под которым круговой сектор занимает центральную часть окружности;
- π - математическая константа, примерное значение которой равно 3,14159.
Давайте разберемся с использованием формулы на примере. Предположим, что нам известна площадь кругового сектора, равная 50 квадратных сантиметров, и угол, под которым он занимает центральную часть окружности, равный 30 градусов. Подставим значения в формулу и произведем необходимые вычисления:
Радиус = квадратный корень ( (50 * 360) / (3,14159 * 30) )
Радиус = квадратный корень ( 18000 / 94,2478 )
Радиус = квадратный корень ( 191.2618 )
Радиус ≈ 13.835 сантиметров
Таким образом, радиус окружности составляет приблизительно 13.835 сантиметров, если известна площадь кругового сектора равная 50 квадратных сантиметров и угол, под которым он занимает центральную часть окружности, равный 30 градусов.
Что такое радиус окружности?
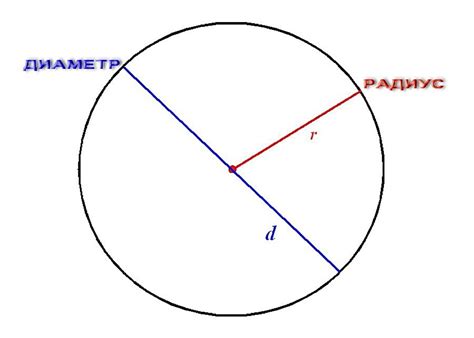
Радиус обозначается символом "R". Вместе с диаметром ("D") и окружностью ("C") он помогает определить все основные характеристики окружности. Радиус можно найти, зная диаметр или окружность, а также площадь или длину дуги кругового сектора.
Например, для нахождения площади кругового сектора, нам нужно знать длину радиуса. Без радиуса невозможно провести также другие геометрические конструкции, такие как построение касательной или определение перекрывания окружностей.
Радиус окружности играет ключевую роль во многих областях знания, включая геометрию, физику, инженерию и естественные науки. Понимание понятия радиуса окружности является основой для решения различных задач и построения математических моделей в этих областях.
Определение и основные понятия
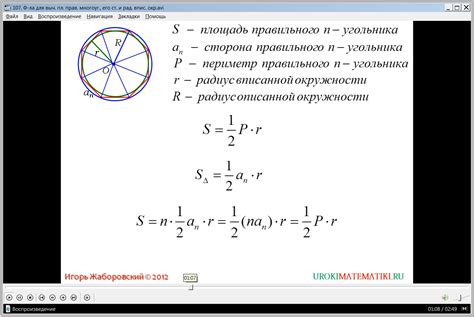
В геометрии круговой сектор представляет собой часть плоскости, ограниченную двумя радиусами и дугой окружности. Этот сектор имеет известную площадь, которую можно использовать для вычисления радиуса окружности, на основе которой строится сектор.
Площадь кругового сектора может быть вычислена с помощью формулы:
S = (П/360) * Пи * r^2,
где S - площадь сектора, Пи - математическая константа, равная приблизительно 3,14159, r - радиус окружности.
Радиус окружности, в свою очередь, можно найти, переставляя элементы в уравнении и решая его относительно радиуса:
r = корень из (S * (360/П) )
где r - радиус окружности, S - площадь кругового сектора, Пи - математическая константа, равная приблизительно 3,14159.
При вычислении радиуса окружности по площади кругового сектора необходимо учесть, что исходная площадь может быть выражена в различных единицах измерения (например, квадратных метрах или квадратных сантиметрах), поэтому необходимо использовать соответствующую систему единиц для получения правильного результата.
Приведенная формула и примеры вычислений позволяют определить радиус окружности по известной площади кругового сектора, что является важным элементом для решения различных геометрических задач и конструкций.
Как вычислить площадь кругового сектора?

Площадь кругового сектора может быть вычислена с использованием формулы:
S = (π * r^2 * φ) / 360
Где:
- S - площадь кругового сектора
- π (пи) - математическая константа, примерное значение равно 3.14
- r - радиус окружности
- φ - центральный угол, измеряемый в градусах
Для вычисления площади кругового сектора необходимо знать значение радиуса окружности и меру угла, которую охватывает сектор. Вычисление площади кругового сектора может быть полезно при решении различных геометрических задач, например, при расчете площади фигуры, ограниченной несколькими секторами окружности.
Важно помнить, что значения радиуса и центрального угла должны быть выражены в одинаковых единицах измерения. Вычисляя площадь кругового сектора, необходимо также обратить внимание на точность результатов, учитывая ограниченное значение числа π.
Вот пример вычисления площади кругового сектора:
Радиус окружности: r = 5 см
Центральный угол: φ = 60°
Подставим значения в формулу:
S = (3.14 * 5^2 * 60) / 360
S = (3.14 * 25 * 60) / 360
S = (3.14 * 1500) / 360
S ≈ 13.09 см²
Таким образом, площадь кругового сектора при радиусе окружности 5 см и центральном угле 60° составляет примерно 13.09 см².
Формула для вычисления площади
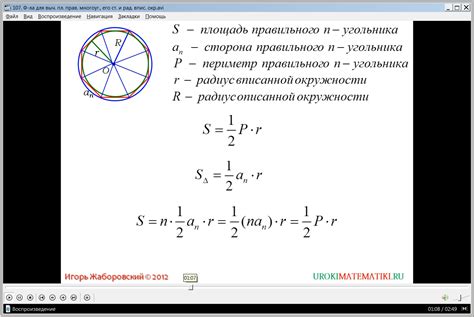
Площадь кругового сектора может быть вычислена с использованием следующей формулы:
S = (π * r^2 * α) / (2 * π) = (r^2 * α) / 2
где:
- S - площадь кругового сектора
- r - радиус окружности
- α - центральный угол, измеряемый в радианах
- π (пи) - математическая константа, приближенно равная 3.14159
Данная формула позволяет вычислить площадь кругового сектора, исходя из значения радиуса и центрального угла. Результат вычисления будет представлять собой численное значение площади в квадратных единицах.
Как найти радиус окружности по площади кругового сектора?

Для нахождения радиуса окружности по площади кругового сектора необходимо знать формулу для вычисления площади сектора и расставить известные значения. Формула для нахождения площади кругового сектора S с радиусом r и центральным углом α выглядит следующим образом:
S = (π * r² * α) / 360°
Для нахождения радиуса окружности по площади кругового сектора необходимо преобразовать формулу, чтобы избавиться от неизвестного значения радиуса:
r = √((S * 360°) / (π * α))
Где:
r - радиус окружности,
S - площадь кругового сектора,
π - число π (пи), примерное значение 3.14159,
α - центральный угол в градусах.
Давайте рассмотрим пример вычисления радиуса окружности по площади кругового сектора:
Пусть площадь сектора S = 25 кв. см и центральный угол α = 90°.
Мы можем использовать формулу для вычисления радиуса:
r = √((25 * 360°) / (3.14159 * 90°))
После вычислений получаем:
r ≈ 3,18 см
Таким образом, радиус окружности примерно равен 3,18 см при заданных значениях площади кругового сектора и центрального угла.
Формула для вычисления радиуса

Для вычисления радиуса окружности по заданной площади кругового сектора используется следующая формула:
- Найдите площадь кругового сектора, зная центральный угол и площадь всего круга.
- Пользуясь формулой для площади кругового сектора, найдите длину радиуса сектора.
- Искомый радиус окружности будет равен квадратному корню из найденной длины радиуса кругового сектора.
Формула вычисления радиуса окружности по площади кругового сектора выглядит следующим образом:
r = √(S/π)
где:
- r - радиус окружности;
- S - площадь кругового сектора;
- π - математическая константа пи, приближенное значение которой равно 3.14159.
Данная формула позволяет определить радиус окружности по известной площади кругового сектора, позволяя более точно рассчитывать геометрические параметры окружностей и круговых секторов.
Примеры вычислений радиуса окружности
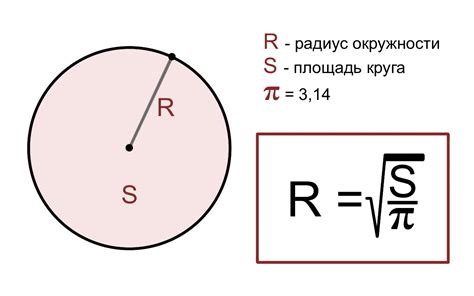
Ниже приведены несколько примеров вычисления радиуса окружности по известной площади кругового сектора:
Пример 1:
Площадь кругового сектора равна 25 квадратных сантиметров. Вычислим радиус окружности.
Формула для вычисления радиуса окружности по площади кругового сектора: Радиус = √(Площадь / π)
Решение: Радиус = √(25 / π) ≈ √(7.957) ≈ 2.82 сантиметра
Ответ: Радиус окружности равен примерно 2.82 сантиметра
Пример 2:
Площадь кругового сектора равна 50 квадратных метров. Найдем радиус окружности.
Формула для вычисления радиуса окружности по площади кругового сектора: Радиус = √(Площадь / π)
Решение: Радиус = √(50 / π) ≈ √(15.915) ≈ 3.99 метра
Ответ: Радиус окружности равен примерно 3.99 метра
Пример 3:
Площадь кругового сектора составляет 100 квадратных дециметров. Вычислим радиус окружности.
Формула для вычисления радиуса окружности по площади кругового сектора: Радиус = √(Площадь / π)
Решение: Радиус = √(100 / π) ≈ √(31.830) ≈ 5.64 дециметра
Ответ: Радиус окружности равен примерно 5.64 дециметра
Пример 1: вычисление радиуса по известной площади
Предположим, у нас есть круговой сектор с известной площадью. Нам необходимо вычислить радиус данной окружности. Для этого мы можем воспользоваться следующей формулой:
Радиус = √(Площадь / π)
Где:
- Радиус - искомая величина
- Площадь - известная площадь кругового сектора
- π - математическая константа, приближенное значение которой равно 3.14
Давайте рассмотрим конкретный пример:
Пусть площадь кругового сектора равна 25 квадратных сантиметров. Чтобы вычислить радиус, мы подставляем значения в формулу:
Радиус = √(25 / 3.14) ≈ √7.96 ≈ 2.82 сантиметра
Таким образом, радиус данной окружности составляет примерно 2.82 сантиметра.
Пример 2: вычисление радиуса по известному углу и длине дуги
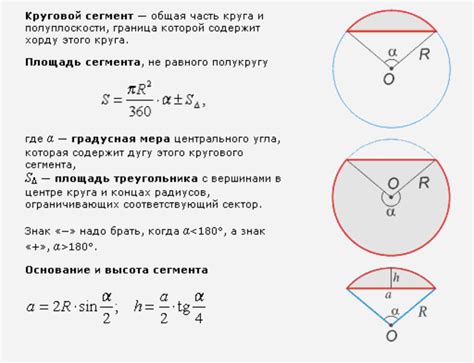
Иногда нам известны угол, под которым виден круговой сектор, и длина дуги этого сектора. В таком случае можно использовать эти данные для вычисления радиуса окружности.
Для начала, нам нужно записать формулы, которые связывают угол и длину дуги с радиусом. Эти формулы будут:
Длина дуги: Д = r * α, где Д - длина дуги, r - радиус окружности, α - угол в радианах.
Угол в радианах: α = Д / r.
Итак, допустим, у нас есть круговой сектор, угол которого 3 радиана, а длина дуги этого сектора равна 6 см. Мы можем использовать вторую формулу для вычисления радиуса:
α = Д / r
3 = 6 / r
r = 6 / 3
r = 2
Таким образом, радиус данной окружности равен 2 см.
Учитывайте, что в данном примере мы использовали угол в радианах. Если угол был задан в градусах, он должен быть преобразован в радианы перед вычислением.