Тангенс – это одно из основных тригонометрических отношений, которое играет важную роль в геометрии и математике в целом. Если у вас есть задача, связанная с нахождением тангенса треугольника, и вам даны координаты вершин в виде клеточек на плоскости, то с помощью нескольких простых шагов вы сможете решить эту задачу без особых проблем.
Для начала, обозначим каждую вершину треугольника координатами вида (x, y), где x - это номер столбца, а y - номер строки клеточки на плоскости. Затем, найдем стороны треугольника, используя формулу расстояния между двуми точками в прямоугольной системе координат. Для этого нужно вычислить разницу между значениями координат по оси x и по оси y для каждой пары вершин.
После получения длин всех сторон треугольника, можно приступить к вычислению значения тангенса. Формула для нахождения тангенса треугольника состоит из отношения противолежащего катета (противоположной стороны треугольника) к прилежащему катету (стороне треугольника, инцидентной заданному углу).
Что такое тангенс треугольника?
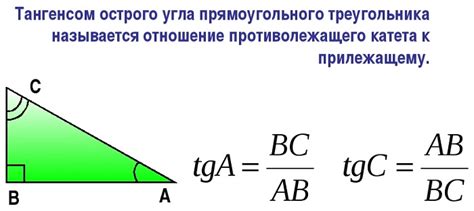
Формула для вычисления тангенса треугольника имеет следующий вид:
| Тангенс треугольника: | tg(α) = (противолежащая сторона) / (прилежащая сторона) |
Здесь α обозначает угол между примыкающей стороной и горизонтальной осью.
Тангенс треугольника может быть положительным или отрицательным, в зависимости от угла α. Если угол α находится в первой или третьей четверти, то тангенс будет положительным. Во второй или четвертой четверти тангенс будет отрицательным.
Знание тангенса треугольника является важным при решении задач, связанных с геометрией, физикой и другими науками. Оно позволяет находить значения неизвестных сторон и углов треугольника по заданным данным.
Раздел 1

Для вычисления тангенса треугольника по клеточкам необходимо знать значение длин сторон треугольника. Для этого можно использовать таблицу, в которой каждая клеточка представляет собой одинаковую единицу измерения.
Построим таблицу размером 3x3:
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
Для вычисления тангенса треугольника сначала найдем длины его сторон:
Длина стороны AB = 2 клеточки (от 1 до 3)
Длина стороны BC = 3 клеточки (от 3 до 9)
Длина стороны CA = 4 клеточки (от 9 до 7)
Зная длины сторон треугольника, можно вычислить его тангенс по формуле:
Тангенс треугольника ABC = Длина стороны AB / Длина стороны BC
Какие данные нужны для нахождения тангенса треугольника?

Для нахождения тангенса треугольника необходимо знать значения двух сторон треугольника и угла между ними.
Тангенс треугольника вычисляется как отношение противоположной стороны к прилежащей стороне, где противоположная сторона это сторона, противолежащая углу, а прилежащая сторона это сторона, прилегающая к углу. То есть, для вычисления тангенса треугольника, нужно знать длину стороны, противолежащей углу, и длину стороны, прилегающей к углу.
Зная значения сторон треугольника и угла между ними, можно применить тригонометрическую функцию тангенса, чтобы вычислить значение тангенса треугольника.
Раздел 2

Как найти тангенс треугольника по клеточкам
Теперь, когда мы знаем значения сторон треугольника, можно рассчитать его тангенс. Тангенс - это отношение противоположной стороны к прилежащей стороне. Для этого нужно взять значение противоположной стороны и разделить его на значение прилежащей стороны.
Формула для расчета тангенса треугольника:
тангенс = противоположная сторона / прилежащая сторона
По ранее найденным значениям, подставим их в формулу и выполним вычисления:
тангенс = (значение противоположной стороны) / (значение прилежащей стороны)
Таким образом, мы можем найти тангенс треугольника, используя известные длины его сторон.
Как найти значение тангенса треугольника?

- Измерьте длины противолежащего катета (сторону, лежащую напротив угла, для которого вы хотите найти тангенс) и прилежащего катета (сторону, прилегающую к углу).
- Разделите длину противолежащего катета на длину прилежащего катета.
- Полученное значение является тангенсом угла треугольника.
Значение тангенса может быть положительным или отрицательным в зависимости от положения угла в треугольнике или квадранте. Углы с положительным тангенсом находятся в I и III квадрантах, а углы с отрицательным тангенсом - во II и IV квадрантах. Также помните, что значения тангенса близкие к бесконечности считаются вертикальными линиями, а значения близкие к нулю - горизонтальными.
Используя формулу и известные длины катетов, вы можете легко найти значение тангенса треугольника и использовать его в дальнейших вычислениях.
Раздел 3: Как найти тангенс треугольника по клеточкам
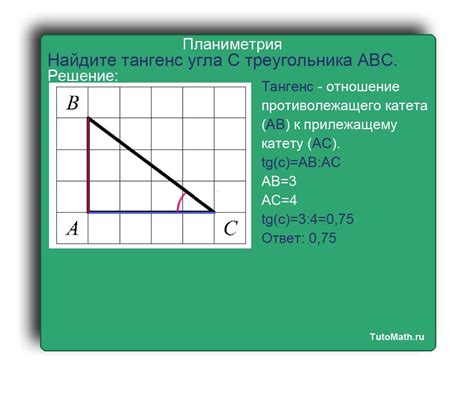
tan(A) = противолежащий катет / прилежащий катет
То есть, чтобы найти тангенс угла A треугольника, нужно разделить значение противолежащего катета на значение прилежащего катета. Полученное значение будет являться тангенсом угла A.
Для нахождения значений катетов и их соотношения между собой, мы можем использовать ранее описанные методы и формулы. После нахождения этих значений, вычисление тангенса становится простым.
Таким образом, в данном разделе мы рассмотрели, как найти тангенс треугольника по клеточкам. Зная значения катетов, можно легко вычислить этот тригонометрический показатель и использовать его в дальнейших расчётах и анализе треугольников.
Способы определить углы треугольника
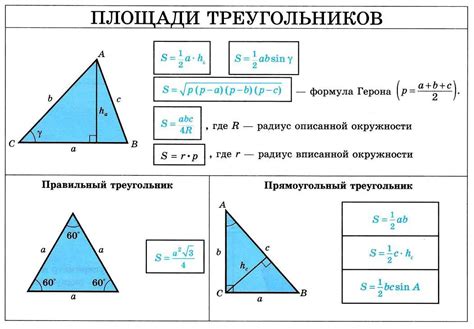
- Использование формулы синусов. Этот метод позволяет определить углы треугольника по длинам его сторон. Формула синусов выглядит следующим образом: sin(A) = a/c, где A - малый угол противоположный стороне a, c - гипотенуза треугольника.
- Использование формулы косинусов. Этот метод позволяет определить углы треугольника по длинам его сторон. Формула косинусов выглядит следующим образом: cos(A) = (b^2 + c^2 - a^2) / (2bc), где A - большой угол противоположный стороне a, b и c - остальные стороны треугольника.
- Использование теоремы Пифагора. Этот метод позволяет определить углы треугольника по длинам его сторон, если треугольник прямоугольный. По теореме Пифагора: a^2 + b^2 = c^2, где a и b - катеты треугольника, c - гипотенуза треугольника.
- Использование известных углов и метода подсчета. Этот метод используется, если некоторые углы треугольника известны. В этом случае, можно использовать сумму углов треугольника (180 градусов) и вычитать из нее известные углы, чтобы определить неизвестные.
Каждый из этих методов имеет свои преимущества и требует определенных условий для использования. Выбор способа определения углов треугольника зависит от известной информации и задачи, которую необходимо решить.