Измерение диагонали квадрата является важной задачей для определения его размеров. Диагональ – это отрезок, соединяющий две противоположные вершины. Нахождение диагонали квадрата может пригодиться в различных ситуациях: от строительства до решения школьных задач.
Существует несколько способов определения диагонали квадрата. Один из самых простых и точных методов заключается в использовании формулы, основанной на его стороне. Если известна длина стороны (a), то диагональ (d) может быть рассчитана по формуле: d = a * √2.
Другой способ заключается в использовании известной площади квадрата. Площадь позволяет найти сторону, а соответствующая сторона - диагональ. Формулу можно определить следующим образом: d = √(2 * S), где S – площадь квадрата.
Не забывайте, что если измеряете диагональ на физическом объекте, то необходимо использовать инструменты для получения точных результатов, как, например, линейка или измерительная лента. При расчете через формулу, желательно использовать калькулятор, чтобы избежать ошибок. Помните, что точные измерения являются ключевыми для успешного использования диагонали квадрата в практических целях.
Как узнать диагональ квадрата: подробное руководство

Если у вас есть одна из сторон квадрата, вы можете найти диагональ с помощью теоремы Пифагора, которую можно представить следующей формулой:
Диагональ квадрата = √(Сторона2 + Сторона2)
Для расчета диагонали квадрата сначала необходимо возвести длину его стороны в квадрат, затем сложить два значения и извлечь квадратный корень получившейся суммы. Результат будет равен длине диагонали квадрата.
Ниже приведена таблица с примерами расчета диагонали квадрата при разных значениях стороны:
| Сторона квадрата | Диагональ квадрата |
|---|---|
| 1 | 1.41 |
| 2 | 2.83 |
| 3 | 4.24 |
| 4 | 5.66 |
Например, если сторона квадрата равна 5, применяя указанную формулу, мы получим следующий результат: √(52 + 52) = √(25 + 25) = √50 ≈ 7.07. Следовательно, диагональ квадрата равна примерно 7.07.
Теперь, с простыми инструкциями и формулой, вы сможете легко и точно определить диагональ квадрата при известной стороне. Это позволит вам выполнять различные задачи, связанные с геометрией и строительством.
Инструменты для измерения диагонали квадрата

Если вам необходимо измерить диагональ квадрата, вам понадобится набор простых инструментов. Независимо от того, используете ли вы профессиональное оборудование или простые средства, такие как линейка и уровень, точные измерения обеспечат правильные результаты.
Ниже приведен список основных инструментов, которые можно использовать для измерения диагонали квадрата:
- Линейка: это самый простой инструмент, используемый для измерений. Найдите линейку с четкими делениями и достаточной длиной для измерения диагонали квадрата.
- Уровень: уровень может быть полезен при измерении диагонали квадрата, особенно если у вас нет достаточно длинной линейки. Приложите уровень вдоль стороны квадрата и продолжайте его через центр, чтобы найти длину диагонали.
- Измерительная лента: если у вас есть достаточно длинная измерительная лента, вы можете использовать ее для измерения диагонали квадрата. Просто протяните ленту через центр квадрата, чтобы получить точные измерения.
- Лазерный измеритель: современные технологии позволяют использовать лазерные измерители для точного измерения. Просто наведите лазер на две противоположные стороны квадрата и измерьте длину диагонали.
Вне зависимости от выбранного инструмента, важно удостовериться, что вы правильно натягиваете или стабилизируете измерительный инструмент, чтобы получить наиболее точные измерения. Также помните, что использование нескольких инструментов для сравнения результатов может помочь подтвердить точность вашего измерения.
Точный способ измерения диагонали квадрата: шаги

- Возьмите линейку или мерную ленту, которая может измерять в сантиметрах или дюймах.
- Расположите квадрат на плоской поверхности таким образом, чтобы все его стороны были ровно параллельны и перпендикулярны друг другу.
- Выберите любую сторону квадрата и измерьте ее длину. Запишите это значение для дальнейшего использования.
- Возьмите линейку или мерную ленту и разместите ее по диагонали квадрата, начиная от одного угла до противоположного. Убедитесь, что инструмент находится вровень с квадратом и не искажает результаты измерений.
- Проследуйте линейкой или лентой по диагонали и определите точку, где она пересекает противоположный угол квадрата.
- Запишите значение измеренной диагонали.
Теперь вы знаете точный способ измерения диагонали квадрата. Используйте эти инструкции, чтобы получить точные результаты и справиться с геометрическими задачами.
Определение диагонали квадрата по его сторонам
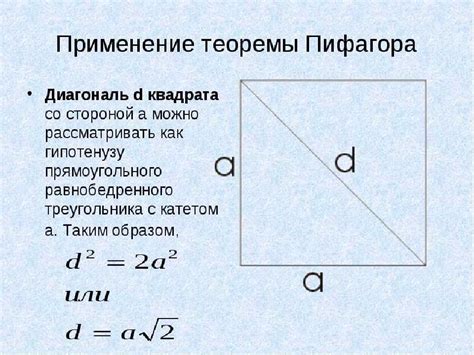
Диагональ квадрата = сторона × √2
Прежде чем применять эту формулу, необходимо знать длину стороны квадрата. Если известна сторона квадрата, можно произвести простой расчет, умножив ее на коэффициент √2.
Например, если сторона квадрата равна 5 см, то диагональ можно определить следующим образом:
Диагональ квадрата = 5 см × √2
Диагональ квадрата ≈ 7,07 см
Таким образом, диагональ квадрата с стороной 5 см составляет около 7,07 см.
Зная формулу и длину стороны, можно легко определить диагональ квадрата и использовать эту информацию для различных задач.
Формула для расчета диагонали квадрата
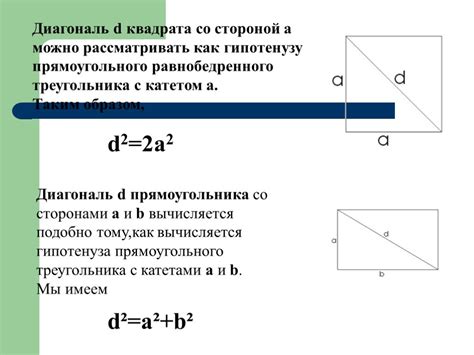
Для расчета диагонали квадрата с известной стороной достаточно использовать простую формулу. Диагональ квадрата можно найти, зная длину одной из его сторон, так как все стороны квадрата равны.
Для нахождения диагонали квадрата, нужно воспользоваться теоремой Пифагора. Если сторона квадрата равна a, то диагональ квадрата равна d и можно воспользоваться формулой:
d = a√2
Здесь символ √2 обозначает квадратный корень из 2. Поэтому умножаем длину одной из сторон на √2, чтобы найти длину диагонали. Например, если сторона квадрата равна 5 сантиметров, то:
d = 5 * √2 ≈ 7.071 сантиметра
Таким образом, длина диагонали квадрата составляет примерно 7.071 сантиметра при стороне 5 сантиметров.
Полезные советы при измерении и расчете диагонали квадрата

1. Используйте правильный инструмент
Для измерения диагонали квадрата лучше всего использовать рулетку или линейку, которые имеют деления в миллиметрах. Это позволит получить более точные и надежные измерения.
2. Установите квадрат на ровную поверхность
Перед измерением диагонали квадрата важно убедиться, что он равномерно и стабильно расположен на ровной поверхности. Это поможет избежать искажений в результатах измерения.
3. Измеряйте диагональ от угла к углу
Для получения наиболее точных результатов измерения необходимо проводить измерение диагонали квадрата от одного угла до другого. Для этого поместите один конец рулетки или линейки в один угол квадрата и проведите ее до противоположного угла.
4. Записывайте результат в миллиметрах
При измерении диагонали квадрата обязательно записывайте полученные значения в миллиметрах, чтобы не потерять результаты и иметь возможность использовать их в дальнейших расчетах.
5. Повторяйте измерение несколько раз
Для обеспечения более точного и надежного результата рекомендуется провести измерение диагонали квадрата несколько раз. При этом следует убедиться, что все измерения дают одинаковый результат. Если есть расхождения, следует повторить измерение или провести дополнительную проверку.
Следуя этим полезным советам, вы сможете правильно измерить и рассчитать диагональ квадрата. Помните, что точность измерений зависит от правильного подхода и использования подходящих инструментов.
Применение знания о диагонали квадрата в практике
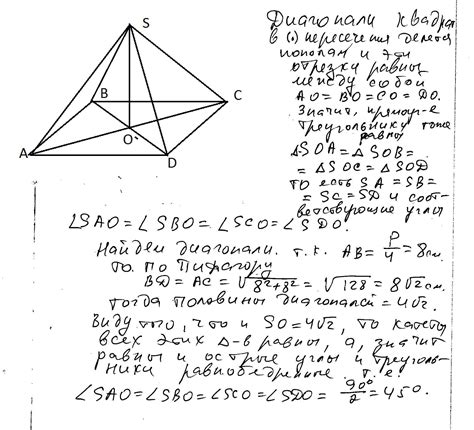
Знание длины диагонали квадрата может быть полезно в различных ситуациях. Рассмотрим некоторые из них:
- Планирование интерьера. Если вы планируете разместить квадратные предметы (например, картину или стол) на стене или полу, знание длины диагонали поможет вам определить оптимальное расстояние между ними. Вы можете использовать формулу диагонали квадрата и применить ее к конкретным измерениям предметов, чтобы получить точные результаты.
- Расчет площади квадратного участка. Если вы занимаетесь садоводством или ландшафтным дизайном, знание длины диагонали квадрата поможет вам расчитать площадь квадратного участка. Для этого можно воспользоваться формулой диагонали и использовать ее вместе с известными измерениями сторон квадрата.
- Фотография и графика. Используя знание длины диагонали квадрата, вы можете создавать эффектные композиции и пропорции в фотографиях и графическом дизайне. Зная длину диагонали, вы можете правильно разместить объекты в кадре и добиться гармоничного визуального впечатления.
Знание и понимание диагонали квадрата помогут вам применять математические концепции и принципы в повседневной жизни. Это полезное знание, которое может быть применено в разных сферах деятельности.