Геометрия - одна из самых увлекательных наук, которая изучает формы, размеры и пространственные отношения объектов. Одним из основных элементов геометрии является треугольник. Он состоит из трех сторон и трех углов, а по нашей задаче нам известны две стороны. Но как найти основание такого треугольника? Этому вопросу мы сегодня посвятим нашу статью.
Известно, что треугольник может быть разных типов, например, прямоугольный, остроугольный или тупоугольный, а основание найти довольно просто. Мы можем воспользоваться теоремой Пифагора, которая рассказывает нам о связи между сторонами прямоугольного треугольника. Если известны две стороны треугольника, то можно найти третью сторону по формуле c^2 = a^2 + b^2, где a и b - это известные стороны, а c - гипотенуза.
Чтобы найти основание треугольника, нужно использовать теорему косинусов. Для этого нам понадобятся длины двух известных сторон и угол между ними. Формула для вычисления основания треугольника выглядит следующим образом: a^2 = b^2 + c^2 - 2bc * cosA, где a - это основание, b и c - известные стороны, а A - угол между ними.
Метод Пифагора и теорема косинусов
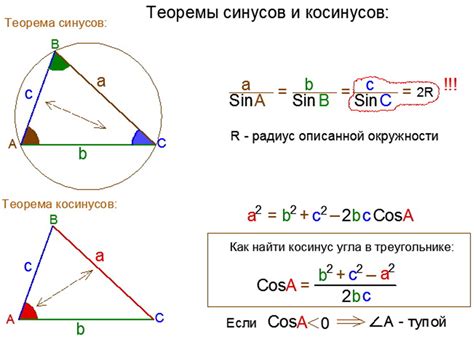
Метод Пифагора, названный в честь древнегреческого математика Пифагора, применяется для нахождения третьего неизвестного катета прямоугольного треугольника. Если мы знаем длину двух сторон треугольника, то с помощью теоремы Пифагора можно найти длину третьего катета.
Теорема Пифагора гласит: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. То есть, если a и b - длины катетов, а c - длина гипотенузы, то формула будет выглядеть следующим образом: c^2 = a^2 + b^2. Используя эту формулу, можно найти длину третьего катета треугольника.
Теорема косинусов позволяет найти длину третьей стороны треугольника, если известны длины двух других сторон и меры двух углов. Теорема косинусов имеет несколько вариаций, одна из которых гласит: квадрат длины третьей стороны треугольника равен сумме квадратов длин двух других сторон минус удвоенное произведение этих сторон на косинус между ними. Формулу можно записать следующим образом: c^2 = a^2 + b^2 - 2ab * cos(C), где C - мера угла, противолежащего третьей стороне.
Используя метод Пифагора и теорему косинусов, можно находить неизвестные значения сторон треугольников и вычислять их геометрические характеристики. Такие знания могут быть полезными при решении задач в различных областях, например, в архитектуре, машиностроении и геодезии.
Равенство оснований треугольников и сторон
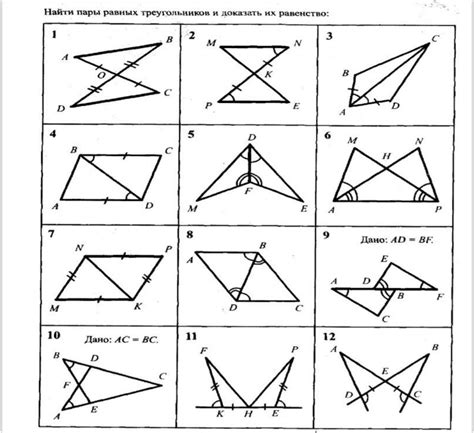
Пусть у нас есть треугольник ABC, у которого известны длины сторон AB и AC. Среди всех возможных треугольников с данными сторонами один из них является равнобедренным, то есть имеет две равные стороны. Зафиксируем основание равнобедренного треугольника и изменим длину его равных сторон, добавив к ним или вычтя из них одинаковые величины. Тогда длина основания и измененные стороны также равны.
Другой способ найти основание треугольника по двум сторонам - воспользоваться теоремой косинусов. Если известны длины двух сторон и угол между ними, то можно найти длину третьей стороны и основание треугольника.
Важно помнить, что существует ограничение на длины сторон треугольника. Сумма длин любых двух сторон треугольника должна быть больше длины третьей стороны. Если это условие не выполняется, треугольник невозможно построить.
Угол между сторонами и основанием: как найти и использовать его

Существует несколько способов найти угол между сторонами и основанием треугольника. Один из самых простых методов - использование теоремы косинусов. Если известны длины всех трех сторон треугольника (a, b и c), то угол между основанием и одной из боковых сторон (угол A) можно найти с помощью следующей формулы:
| Формула | Описание |
|---|---|
| cosA = (b² + c² - a²) / (2bc) | Формула для нахождения косинуса угла A |
Если известны только длины сторон треугольника и необходимо найти угол между основанием и боковой стороной, то можно использовать обратные функции косинуса (арккосинус). Для этого нужно знать значение косинуса угла A и применить такую формулу:
| Формула | Описание |
|---|---|
| A = arccos((b² + c² - a²) / (2bc)) | Формула для нахождения угла A |
Угол между сторонами и основанием треугольника может быть использован в различных вычислениях и построениях. Например, используя этот угол, можно найти высоту треугольника относительно основания или найти площадь треугольника с помощью формулы S = 0.5 * b * c * sinA, где S - площадь треугольника.
Таким образом, угол между сторонами и основанием треугольника играет важную роль в геометрии и может быть легко и точно вычислен с использованием соответствующих формул. С его помощью можно решать различные геометрические задачи и находить различные параметры треугольника.
Высота треугольника и связь с основанием
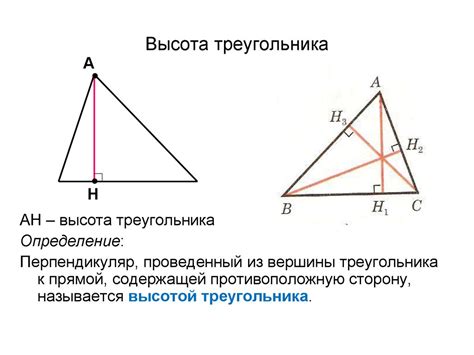
Основание треугольника - это одна из его сторон, на которой лежит высота. Длина основания является важным параметром для расчета площади треугольника или высоты. Чем больше длина основания, тем больше площадь треугольника и высота.
Связь между высотой и основанием треугольника описывается формулой: Площадь треугольника = (основание * высота) / 2. Зная длину основания и площадь треугольника, можно выразить высоту как: Высота = (2 * площадь треугольника) / основание.
Вычисление высоты треугольника по двум сторонам может быть полезно при решении геометрических задач, например, при нахождении площади фигуры или при определении геометрических параметров треугольника.
Построение треугольника по известным сторонам и основанию
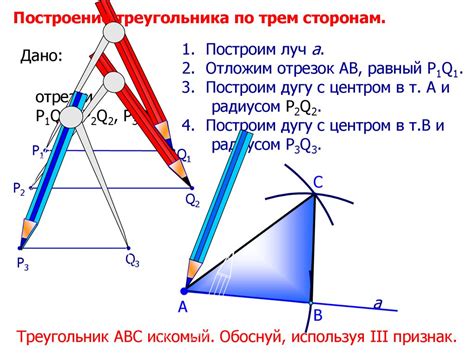
Для построения треугольника по известным сторонам и основанию можно воспользоваться несколькими методами.
- Первый метод основан на использовании теоремы Пифагора. Если известны две стороны треугольника и его основание, то можно найти третью сторону с помощью теоремы Пифагора. Для этого необходимо найти длину боковой стороны, которая будет равна квадратному корню из суммы квадратов длин двух известных сторон.
- Второй метод основан на использовании формулы площади треугольника. Если известны две стороны и высота, опущенная на основание треугольника, то можно вычислить площадь треугольника с помощью формулы: S = (основание * высота) / 2. После этого можно найти третью сторону, зная площадь и длину основания. Для этого необходимо разделить удвоенную площадь на длину основания.
- Третий метод основан на использовании теоремы косинусов. Если известны две стороны и угол между ними, то можно найти третью сторону с помощью теоремы косинусов. Для этого необходимо использовать следующую формулу: c^2 = a^2 + b^2 - 2ab * cos(C), где c - третья сторона, a и b - известные стороны, C - угол между ними.
Эти методы позволяют находить третью сторону треугольника, если известны две стороны и основание. Важно помнить, что в случае, если данные стороны и основание не могут образовать треугольник, построение будет невозможно.
Формула для вычисления основания треугольника
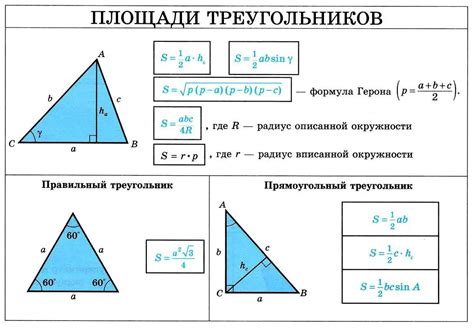
Существует формула, позволяющая вычислить основание треугольника, если известны длины двух его сторон и угол между ними. Для этого можно воспользоваться теоремой косинусов:
| Формула | Примечание |
|---|---|
| a = √((b)2 + (c)2 - 2bccos(α)) | Формула для вычисления основания треугольника |
Где:
- a - основание треугольника
- b и c - длины сторон треугольника
- α - угол между сторонами b и c
Для использования данной формулы необходимо знать длины двух сторон треугольника и значение угла между ними. Зная эти данные, можно рассчитать основание треугольника и использовать его в дальнейших расчетах или решении геометрических задач.
Важно учитывать, что в случае некорректных данных или особых свойств треугольника применение данной формулы может быть ограничено. Поэтому перед использованием формулы необходимо проверить соответствие условиям и особым свойствам треугольника.
Примеры решения задач с поиском основания треугольника

Рассмотрим несколько примеров задач, в которых требуется найти основание треугольника по известным сторонам.
Пример 1:
Дан треугольник ABC, в котором известны длины сторон AB = 5 см и BC = 7 см. Необходимо найти длину основания треугольника AC.
Решение:
Для решения этой задачи можно использовать теорему Пифагора. Сначала найдем длину третьей стороны треугольника. По теореме Пифагора: AB^2 + BC^2 = AC^2. Подставив известные значения, получим: 5^2 + 7^2 = AC^2. Вычислив правую часть уравнения, получаем 74 = AC^2. Извлекая квадратный корень из обеих частей уравнения, получим AC ≈ 8,6 см. Таким образом, длина основания треугольника AC приближенно равна 8,6 см.
Пример 2:
Рассмотрим треугольник XYZ, в котором известны длины сторон XY = 4 см и YZ = 6 см. Найдем длину основания треугольника XZ.
Решение:
Для решения этой задачи можно использовать теорему косинусов. Найдем угол XYZ по формуле: cos(XYZ) = (XY^2 + YZ^2 - XZ^2) / (2 * XY * YZ). Подставив известные значения, получим: cos(XYZ) ≈ (4^2 + 6^2 - XZ^2) / (2 * 4 * 6). Вычислив правую часть уравнения, получаем: XZ^2 ≈ 52 - 48 * cos(XYZ). Зная значение косинуса угла XYZ, можно вычислить значение XZ. Таким образом, длина основания треугольника XZ будет зависеть от значений углов и будет равна примерно 2,8 см.
Таким образом, за счет использования различных геометрических теорем и формул, можно решать задачи с поиском основания треугольника по известным сторонам.
Практическое применение: построение фигур с использованием основания треугольника

Рассмотрим пример. Пусть у нас есть треугольник ABC, где сторона AB = 5 см, сторона AC = 4 см, а угол ABC = 60 градусов. Найдем длину основания BC.
Для нахождения длины основания воспользуемся теоремой косинусов. Она гласит:
c^2 = a^2 + b^2 - 2ab * cos(C), где
c - длина основания (BC)
a, b - длины сторон треугольника (AB, AC)
C - угол при основании треугольника (ABC)
| Дано: | Решение: |
|---|---|
| a = 5 см | c^2 = 5^2 + 4^2 - 2*5*4*cos(60) |
| b = 4 см | c^2 = 25 + 16 - 40 * 0.5 |
| C = 60 градусов | c^2 = 25 + 16 - 20 |
| c^2 = 21 | |
| c = √21 |
Таким образом, длина основания треугольника BC равна корню из 21, что примерно равно 4.58 см. Используя полученное значение, мы можем построить различные фигуры, например, параллелограмм или трапецию.