Квадрат - одна из самых простых и известных геометрических фигур. Его стороны равны друг другу и перпендикулярны. Для нахождения стороны квадрата по диагонали существует специальная формула, которая помогает решить эту задачу.
Прежде чем мы перейдем к формуле, давайте разберемся, что такое диагональ квадрата. Диагональ - это отрезок, соединяющий две противоположные вершины квадрата. Она проходит через его центр и делит его на два равных треугольника.
Для того чтобы найти сторону квадрата по известной длине диагонали, мы можем воспользоваться пифагоровой теоремой. В данном случае, мы знаем длину гипотенузы, которая равна диагонали квадрата, и хотим найти длину катета, который является стороной квадрата.
Формула для нахождения стороны квадрата по диагонали имеет вид: сторона = диагональ / √2. Она основана на применении пифагоровой теоремы и позволяет найти сторону квадрата, если известна его диагональ.
Что такое квадрат и диагональ?

Диагональ - это отрезок, соединяющий две противоположные вершины квадрата. У квадрата есть две диагонали: главная (проходит через центр квадрата) и побочная.
Для квадрата диагональ является одной из наиболее значимых линий, так как она делит квадрат на два равнобедренных прямоугольных треугольника. Диагональ также является главной линией симметрии квадрата.
Формула для нахождения длины диагонали квадрата по заданной стороне:
- Диагональ квадрата равна длине стороны, умноженной на √2.
Таким образом, для нахождения длины диагонали квадрата нужно умножить длину стороны на √2. Формула выглядит следующим образом:
Диагональ = Сторона × √2.
Определение квадрата и диагонали
Для определения длины стороны квадрата по заданной диагонали можно использовать формулу. Пусть "d" - это длина диагонали, а "a" - это длина стороны квадрата:
| Формула | a = d / √2 |
Однако, для определения стороны квадрата по диагонали нам необходимо знать длину диагонали, которую можно измерить или указать в условии задачи. Используя эту формулу, мы можем вычислить сторону квадрата и получить ответ на поставленную задачу.
Таким образом, зная длину диагонали квадрата, мы можем легко определить длину его стороны с помощью простой математической формулы.
Как найти длину диагонали квадрата?
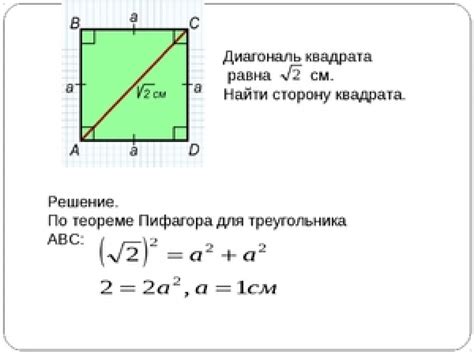
Учитывая, что все стороны квадрата равны между собой, мы можем использовать теорему Пифагора для нахождения длины диагонали. Согласно теореме, квадрат длины диагонали равен сумме квадратов длины двух сторон.
Таким образом, чтобы найти длину диагонали квадрата, мы можем использовать формулу: диагональ = сторона × √2, где √2 – это приближенное значение корня из числа 2.
Например, если известна длина стороны квадрата, мы можем найти длину его диагонали, умножив длину стороны на √2. Обратно, если нам дана длина диагонали, мы можем найти длину стороны, разделив длину диагонали на √2.
Упрощенное объяснение шаг за шагом

Нахождение стороны квадрата по диагонали может показаться сложной задачей, но на самом деле это довольно просто. Давайте рассмотрим шаги по нахождению стороны квадрата по заданной диагонали.
- Возьмите значение диагонали, данной в условии, и запишите его.
- Возведите это значение в квадрат.
- Умножьте полученный результат на 2.
- Извлеките квадратный корень из полученного значения.
Полученный результат будет стороной квадрата по заданной диагонали. Давайте проиллюстрируем это на примере:
- Пусть дана диагональ квадрата, равная 10.
- Возводим это значение в квадрат: 10 * 10 = 100.
- Умножаем полученное значение на 2: 100 * 2 = 200.
- Извлекаем квадратный корень из 200: √200 ≈ 14.14.
Полученный результат 14.14 будет стороной квадрата по заданной диагонали 10.
Таким образом, используя формулу нахождения стороны квадрата по диагонали, можно легко и быстро получить результат. Надеюсь, данное объяснение помогло вам разобраться в этом вопросе!
Формула для нахождения стороны квадрата по диагонали
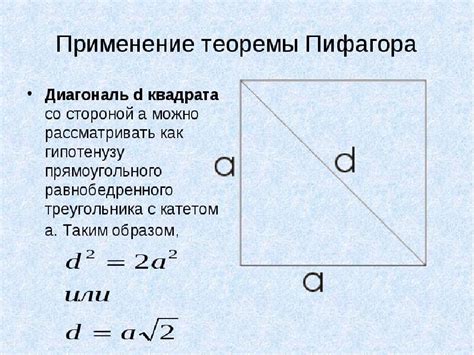
Когда известна диагональ квадрата, есть простая формула, позволяющая найти длину его стороны.
Формула для нахождения стороны квадрата по диагонали выглядит следующим образом:
- Длина стороны квадрата = диагональ / √2
Для использования этой формулы следует знать, что диагональ квадрата - это прямая линия, которая соединяет две противоположные вершины.
По этой простой формуле можно рассчитать сторону квадрата при известной длине диагонали и наоборот.
Теперь мы можем использовать эту формулу для нахождения стороны квадрата, когда нам известна его диагональ.
Математическая формула для решения
Для определения стороны квадрата по известной диагонали можно воспользоваться следующей математической формулой:
Сторона квадрата = Диагональ / √2
Чтобы применить эту формулу, необходимо знать значение диагонали. Подставьте это значение в формулу, затем вычислите результат, и он даст вам длину стороны квадрата.
Например, если известна диагональ квадрата и она равна 10 см:
Сторона квадрата = 10 см / √2 ≈ 7,07 см
Таким образом, сторона квадрата будет примерно равна 7,07 см.