Треугольная призма - это трехмерная геометрическая фигура, состоящая из треугольного основания и трех боковых граней, которые соединяются в вершине. Найти объем такой призмы может показаться сложной задачей, но на самом деле это относительно просто при наличии определенных измерений.
Для того чтобы вычислить объем треугольной призмы, необходимо знать длину основания, высоту призмы и длину бокового ребра. Если вы не знаете эти значения, то перед началом измерений вам понадобится линейка или другие измерительные инструменты.
Первоначально определите длину основания и отметьте ее на листе бумаги или другой поверхности. Затем, используя линейку или измерительную ленту, измерьте высоту призмы - этот параметр является перпендикулярным расстоянием между основанием и вершиной. Наконец, измерьте длину бокового ребра, которое связывает верхнюю вершину с подставкой призмы.
Изучение формулы объема треугольной призмы
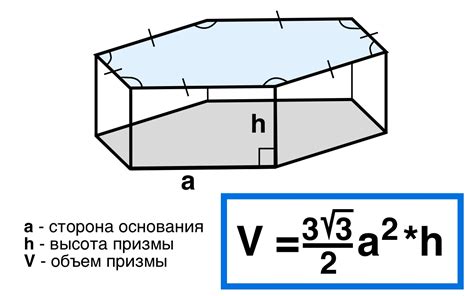
Треугольная призма состоит из трех треугольников вокруг одной общей вершины. Одна из этих трех граней является основанием призмы, а две другие - боковыми гранями. Стороны основания и высота призмы играют ключевую роль в вычислении ее объема.
Формула для вычисления объема треугольной призмы:
V = (площадь основания * высота) / 2
Для вычисления площади основания треугольной призмы необходимо знать длины двух сторон основания и угол между ними. После вычисления площади основания и измерения высоты призмы, мы можем использовать эту формулу для получения объема.
Изучение формулы объема треугольной призмы поможет вам решать различные задачи, связанные с геометрией и пространственным мышлением. Это также может быть полезным при работе с трехмерной графикой, архитектурным проектированием и другими областями, где требуется понимание объема и форм трехмерных объектов.
Необходимо отметить, что формула объема треугольной призмы имеет свои ограничения и может не подходить для некоторых сложных трехмерных фигур. Для этих случаев существуют другие методы вычисления объема.
Определение треугольной призмы и ее особенности
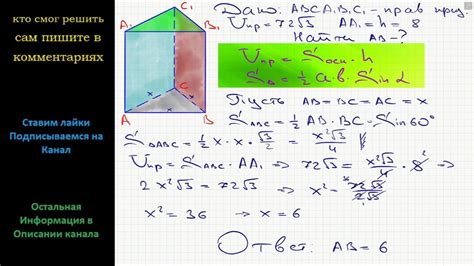
Основной особенностью треугольной призмы является ее форма. Она отличается от других призм, таких как прямоугольная или пятиугольная, тем, что имеет треугольные основания. Это делает треугольную призму особенно полезной в различных математических и инженерных расчетах и приложениях.
Объем треугольной призмы можно вычислить, умножив площадь одного из оснований на высоту призмы. Вычисление площади одного из оснований треугольной призмы может потребовать использования тригонометрии, если основание не является прямоугольным.
Изучение треугольных призм является важным элементом в образовании и практических расчетах. Оно позволяет понять и применять геометрические принципы для решения задач, связанных с объемами и площадями трехмерных фигур.
Перечень необходимых измерений и параметров
При вычислении объема треугольной призмы необходимо знать следующие измерения и параметры:
1. Длина основания треугольника - это одна из сторон треугольной призмы, которая образует основу треугольника.
2. Высота треугольника - это линия, перпендикулярная основанию, соединяющая его с вершиной треугольника.
3. Длина боковой стороны треугольника - это сторона треугольника, которая не является основой и соединяет две вершины.
4. Высота призмы - это расстояние между основанием и верхней плоскостью призмы, перпендикулярное им.
5. Угол между основанием призмы и боковой стороной - это угол, образованный основанием и соответствующей боковой стороной треугольной призмы.
В сочетании этих измерений и параметров вы сможете точно вычислить объем треугольной призмы и использовать его для различных целей.
Подсчет площади основания треугольной призмы

Площадь основания треугольной призмы может быть рассчитана путем умножения длины основания на высоту, а затем делением полученного значения на 2. Формула для расчета площади основания: Площадь = (длина основания * высота) / 2.
Для вычисления площади основания треугольной призмы, необходимо знать длину основания и высоту треугольника.
Пример:
Предположим, у нас есть треугольная призма с основанием длиной 8 см и высотой 6 см. Чтобы найти площадь основания, мы используем формулу: площадь = (8 * 6) / 2 = 24 квадратных см.
Теперь, когда мы знаем, как вычислить площадь основания треугольной призмы, мы можем использовать этот результат для дальнейших расчетов, например, для определения объема треугольной призмы. Площадь основания необходима для формулы: объем = (площадь основания * высота призмы).
Вычисление высоты треугольной призмы

Используя площадь основания и объем призмы:
1. Найдите площадь основания треугольной призмы, используя соответствующую формулу для треугольника.
2. Вычислите объем призмы, используя формулу V = S * h, где V - объем, S - площадь основания и h - высота.
3. Решите уравнение относительно высоты, разрешив его относительно h: h = V / S.
Используя длины сторон треугольника:
1. Найдите площадь основания треугольника, используя формулу для треугольника.
2. Найдите площадь боковой поверхности призмы, используя формулу Sb = (a * h) / 2, где Sb - площадь боковой поверхности, a - длина стороны основания и h - высота.
3. Найдите объем призмы, используя формулу V = S * h, где V - объем, S - площадь основания и h - высота.
4. Решите уравнение относительно высоты, подставив известные значения: h = (2 * V) / Sb.
Используя один из этих методов, вы можете вычислить высоту треугольной призмы и использовать ее в дальнейших расчетах и измерениях.
Применение формулы объема треугольной призмы
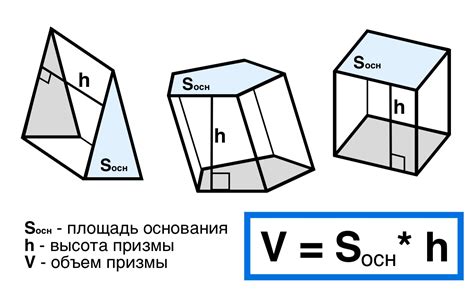
Формула для расчета объема треугольной призмы определена следующим образом:
V = (1/2) * a * b * h
Где:
- V - объем призмы,
- a - длина основания призмы,
- b - ширина основания призмы,
- h - высота призмы.
Для применения этой формулы необходимо знать значения всех параметров призмы. Длина и ширина основания могут быть определены с помощью соответствующих измерений. Высоту можно измерить или получить из других источников данных.
После того как все значения известны, формула позволяет вычислить объем треугольной призмы, который измеряется в кубических единицах, таких как кубический сантиметр (см³) или кубический метр (м³).
Применение формулы поможет вам точно определить объем треугольной призмы и использовать эту информацию в различных областях, таких как строительство, производство и геометрия.
Практическое применение полученных результатов

Знание формулы для вычисления объема треугольной призмы может быть полезным во многих практических ситуациях. Ниже приведены несколько примеров, где вы можете использовать эту формулу:
1. Архитектура и строительство:
При проектировании зданий и сооружений инженеры часто сталкиваются с необходимостью определения объема треугольных призм. Например, при расчете объема треугольной крыши или фасада здания.
2. Дизайн и искусство:
Художники и дизайнеры также могут использовать формулу для определения объема треугольной призмы, чтобы создать уникальные и эстетически привлекательные формы и объекты.
3. Геометрические вычисления:
Понимание формулы позволяет проводить различные геометрические вычисления, например, находить объемы нестандартных трехмерных фигур и тел.
4. Кулинария:
Формула для вычисления объема треугольной призмы может быть полезна в кулинарии, при расчете объема и веса кондитерских изделий с нестандартными формами.
Умение применять формулу для вычисления объема треугольной призмы открывает много возможностей для творческого применения математики в реальной жизни. Независимо от того, в какой области вы работаете или учитесть, эти знания могут быть полезными и способствовать вашему профессиональному росту.