Куб квадрата – это математическое понятие, которое означает возведение числа, представленного квадратом, в третью степень. Это не только интересный математический факт, но и очень полезное знание в повседневной жизни. Узнать куб квадрата несложно, если знать некоторые основные математические операции.
Для начала, необходимо знать, как возвести число в степень. При возведении числа в куб, оно умножается само на себя три раза. Математически это можно записать в виде формулы: а в кубе = а * а * а. Например, если число а = 4, то его куб будет равен 4 * 4 * 4 = 64.
Если у вас нет калькулятора под рукой, есть способ узнать куб квадрата без использования технических средств. Вам просто нужно запомнить первые десять чисел в кубе, а затем умножить число, представленное квадратом, на себя три раза. Например, куб числа 7 будет равен 7 * 7 * 7 = 343.
Что такое куб квадрата?
Для вычисления объема куба квадрата необходимо умножить длину одной из его сторон в квадрате на саму сторону: V = a^3, где V - объем куба квадрата, a - длина стороны.
Куб квадрата является одной из базовых и наиболее простых форм в трехмерной геометрии. У него есть множество применений в различных областях, включая архитектуру, инженерию и математику.
Почему важно узнать куб квадрата?
Когда мы говорим о кубе квадрата, мы относимся к процессу возведения квадрата в третью степень. Возведение в куб квадрата позволяет нам определить его объем и площадь поверхности, а также понять его особенности и свойства.
Знание куба квадрата особенно полезно при решении различных задач, связанных с геометрией и математикой. Например, при вычислении объема кубических объектов, при нахождении длины ребра куба или при изучении свойств кубических уравнений.
Кроме того, понимание куба квадрата помогает нам увидеть его связь с другими геометрическими фигурами, такими как параллелепипеды, призмы и даже окружности. Это позволяет нам лучше анализировать и решать задачи, связанные с этими фигурами.
Наконец, знание куба квадрата дает нам возможность лучше понять пространственные и геометрические концепции, что является важным для нашего интеллектуального развития и познания окружающего мира. Поэтому, узнавая куб квадрата, мы расширяем свои знания в математике и геометрии, что оказывается полезным в различных сферах жизни.
Шаг 1: Изучите задачу внимательно
Перед тем, как решать задачу на нахождение куба квадрата, необходимо внимательно изучить ее условие. Убедитесь, что вы полностью понимаете, что от вас требуется.
В задаче может быть дано число, для которого необходимо найти куб квадрата, или может быть дана некая формула, которую нужно использовать для нахождения результата. Перечитайте условие несколько раз, чтобы избежать путаницы и ошибок в процессе работы.
Если в условии задачи использованы неизвестные термины или формулы, проведите дополнительные исследования и пояснения. Вы можете обратиться к учебнику или преподавателю для уточнения неясностей.
Также обратите внимание на то, какое значение должен иметь результат. Возможно, в задании указаны определенные условия, которые нужно учесть при решении. Подобное понимание поможет вам выбрать правильный подход к решению и получить верный ответ.
Перед тем, как переходить к следующему шагу, удостоверьтесь, что вы полностью разобрались в задаче и уверены в понимании ее условия. Только в таком случае вы сможете приступить к последующим этапам и найти правильное решение.
Шаг 2: Найдите сторону квадрата
Чтобы найти сторону квадрата, нужно извлечь квадратный корень из площади квадрата. Площадь квадрата равна произведению длины его стороны на саму себя.
Если известна площадь квадрата, обозначим ее как S, то сторона квадрата будет равна квадратному корню из S.
Формула для нахождения стороны квадрата выглядит следующим образом:
a = √S
Где a - сторона квадрата, а S - площадь квадрата.
Например, если площадь квадрата равна 25 квадратных сантиметров, то сторона квадрата будет равна 5 сантиметрам, так как квадратный корень из 25 равен 5.
Теперь, когда мы знаем, как найти сторону квадрата, мы можем перейти к следующему шагу - нахождению куба этой стороны.
Шаг 3: Возведите сторону квадрата в куб
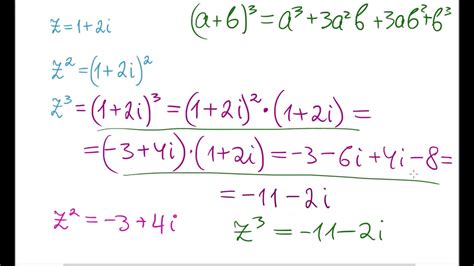
Теперь, когда у вас есть длина стороны квадрата, вы можете возвести ее в куб, чтобы найти объем куба.
Для этого умножьте значение стороны на саму себя два раза:
сторона3
Например, если сторона квадрата равна 4 см:
43 = 4*4*4 = 64
Таким образом, объем куба с стороной 4 см будет равен 64 кубическим сантиметрам.
Шаг 4: Полученный результат - это и есть куб квадрата!
Четвёртый шаг очень простой: нужно возвести полученное значение в квадрат ещё раз.
Если мы изначально нашли квадрат числа, то когда возводим его во вторую степень, полученный результат будет именно кубом этого числа.
Пример:
Допустим, мы посчитали, что квадрат 5 равен 25. Теперь нужно возвести это значение в квадрат ещё раз:
25 * 25 = 625.
Таким образом, куб квадрата числа 5 равен 625.
Подведение итогов и дополнительные советы

Теперь, когда вы овладели навыком нахождения куба квадрата, давайте подведем итоги и дадим несколько дополнительных советов:
- В суть данного метода входит простой и понятный алгоритм. Сначала нужно возвести число в квадрат, а затем полученный результат возвести в куб. Это позволяет ускорить процесс вычисления и избежать ошибок.
- Не забывайте использовать правила алгебры при выполнении вычислений. Например, при перемножении двух одинаковых чисел возводящихся в степень, можно заменить их на число, возведенное в степень суммы их показателей.
- Обратите внимание на порядок операций в формуле. Возвести квадрат в куб - это значит сначала возвести число в квадрат, а затем полученный результат возвести в куб.
- Не забывайте проверять правильность решения с помощью калькулятора или специальных программ для вычисления степеней.
- Практика делает мастера. Чем больше примеров вы решите, тем лучше вы усвоите этот метод и научитесь применять его на практике.
Теперь вы готовы применить полученные знания и находить куб квадрата с легкостью. Этот навык пригодится вам не только в учебе, но и в повседневной жизни.