Вычисление периметра круга - одна из фундаментальных задач в математике. Периметр (или окружность круга) представляет собой длину замкнутой кривой, ограничивающей его площадь. Для вычисления периметра круга по его диаметру необходимо знать несколько основных формул и правил.
Диаметр круга - это прямая линия, проходящая через его центр и две противоположные точки на окружности. Диаметр обозначается символом "d". Перисмя константы "пи" (π) использован в математике для вычисления окружности и других геометрических фигур. Значение "пи" примерно равно 3,14159. В зависимости от точности, которую требуется в вычислениях, можно использовать различное число знаков после запятой для числа "пи".
Формула для вычисления периметра круга по его диаметру выглядит следующим образом: P = π * d. Здесь "P" - это периметр, "π" - число пи, "d" - диаметр круга. Для вычисления периметра круга достаточно знать значение диаметра и умножить его на значение числа "пи". Полученное число будет представлять собой периметр круга в выбранных единицах измерения.
Зачем нужно вычислить периметр круга?

Вычисление периметра круга позволяет:
- Определить длину провода или трубы, необходимую для обведения или оборудования окружности;
- Рассчитать необходимую длину ленты или бордюра для создания круглого цветника или декоративной клумбы;
- Оценить объем нужного материала (например, линолеума или обоев) для покрытия пола или стен в комнате, имеющей форму окружности;
- Избежать излишних затрат, связанных с недостаточным или избыточным количеством материала при строительстве или ремонте;
- Рассчитать пропускную способность канала или трубы для определенного объема жидкости или газа;
- Получить более точные расчёты в различных учебных задачах, связанных с геометрией и физикой.
Точное вычисление периметра круга по его диаметру позволяет решать эти и другие задачи с высокой точностью и эффективностью.
Диаметр круга и его значение
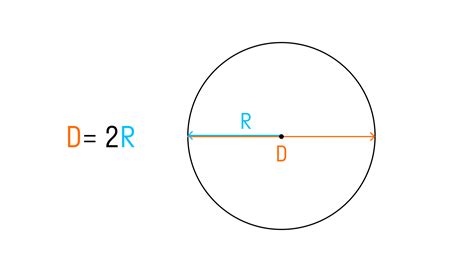
Значение диаметра круга имеет важное значение при вычислении различных параметров круга, таких как площадь, длина окружности и радиус. Диаметр также влияет на периметр круга, который является суммой длин окружностей двух полуокружностей.
Для вычисления периметра круга по его диаметру можно использовать формулу:
Периметр = π * диаметр
Где π (пи) - это математическая константа, равная приблизительно 3,14159.
Что такое периметр круга?

Правило вычисления периметра круга состоит в умножении диаметра окружности на число π (пи). Диаметр окружности равен удвоенному радиусу, который представляет собой расстояние от центра круга до любой его точки на окружности.
Таким образом, формула для вычисления периметра круга выглядит следующим образом:
Периметр круга = диаметр × π
Результат вычисления периметра круга измеряется в тех же единицах длины, что и диаметр. Например, если диаметр указан в сантиметрах, то и периметр будет выражен в сантиметрах.
Формула для вычисления периметра круга
P = π * d
где:
- P - периметр круга;
- π - число пи, которое примерно равно 3.14159 (или можно использовать более точное значение);
- d - диаметр круга, то есть расстояние между двумя точками на его окружности, проходящими через его центр.
Таким образом, чтобы вычислить периметр круга, необходимо умножить диаметр на число пи.
Например, если диаметр круга равен 10 сантиметрам, то его периметр можно вычислить следующим образом:
P = π * 10 = 3.14159 * 10 ≈ 31.4159 см.
Таким образом, периметр этого круга будет примерно равен 31.4159 сантиметра.
Как использовать формулу?
Формула для вычисления периметра круга по его диаметру:
P = π × D
Где P – периметр круга, D – диаметр круга, а π (пи) – математическая константа, примерное значение которой равно 3,14.
Чтобы вычислить периметр круга, необходимо умножить значение диаметра на число π.
Например, если диаметр круга равен 10 сантиметрам, то периметр будет равен:
P = 3,14 × 10 = 31,4 сантиметра
Таким образом, используя простую формулу, можно быстро и легко вычислить периметр круга по его диаметру.
Пример расчета периметра круга

Периметр круга можно найти, зная его диаметр. Для этого нужно воспользоваться формулой:
Периметр круга = π * диаметр
где π (пи) - это математическая константа, которая примерно равна 3.14159...
Для примера, рассмотрим круг с диаметром 10 сантиметров. Чтобы найти периметр, нужно умножить диаметр на π:
Периметр = 3.14159 * 10 см = 31.4159 см
Таким образом, периметр этого круга будет равен примерно 31.4159 сантиметра.
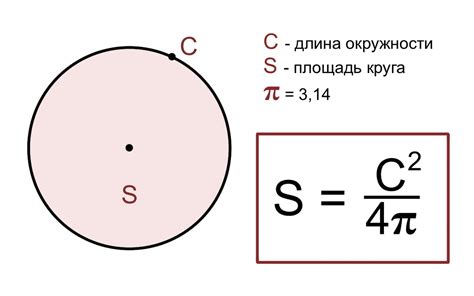
Связь периметра и радиуса круга
Длина окружности вычисляется по формуле: P = 2πr, где P - периметр, π (пи) - математическая постоянная, равная примерно 3.14, r - радиус круга.
Таким образом, периметр круга прямо пропорционален его радиусу. Если увеличить радиус в два раза, периметр также увеличится в два раза. Аналогично, если уменьшить радиус, периметр тоже уменьшится.
Зная диаметр круга, можно легко вычислить радиус, разделив диаметр на 2. Затем, используя формулу, можно вычислить периметр круга.
Например, если диаметр круга равен 10 см, то радиус будет равен 5 см. Подставив значения в формулу P = 2πr, получим P = 2 * 3.14 * 5 = 31.4 см.
Таким образом, периметр круга равен 31.4 см при диаметре 10 см и радиусе 5 см.
Где применяются знания о периметре круга?
Знание о периметре круга находит применение во многих сферах жизни и научных областях. Некоторые из них включают:
- Геометрия и математика: Знание о периметре круга является основополагающим в геометрии и математике. Оно помогает в изучении свойств и формулировании теорий, связанных с кругами и окружностями.
- Архитектура и дизайн: Знание о периметре круга позволяет архитекторам и дизайнерам правильно располагать круглые формы в своих проектах. Также оно используется при расчете длины и ширины окон и дверей.
- Инженерное дело: В инженерных расчетах знание о периметре круга используется для определения длины кабелей, трубопроводов и других объектов, имеющих форму круга.
- Физика и астрономия: При изучении законов физики и астрономии знание о периметре круга позволяет определить длину орбит планет и спутников, а также расстояние между ними.
- Производство и технологии: В процессе производства различных изделий, таких как колеса, диски, крышки и другие предметы с круглой формой, необходимо знание о периметре круга для правильного расчета размеров и материалов.
- Развлечения: Знание о периметре круга может быть использовано в различных играх и головоломках для расчета длины пути или строки, а также для создания графических эффектов.