Куб – это геометрическое тело, состоящее из шести квадратных граней. Он обладает не только объемом и площадью поверхности, но и периметром. Периметр куба можно определить как сумму длин всех его ребер. Знание периметра может быть полезно при решении различных задач, связанных с кубами.
Существует несколько способов вычисления периметра куба. Один из самых простых – это использование формулы, которая связывает периметр куба с длиной его ребра. Для этого нужно знать значение стороны куба, после чего можно просто умножить это значение на 12, так как у куба 12 ребер.
Формула для вычисления периметра куба:
Периметр куба = длина ребра × 12
Например, если длина ребра куба равна 5 см, то периметр можно найти по формуле: 5 см × 12 = 60 см. Таким образом, периметр куба с ребром длиной 5 см будет равен 60 см.
Также можно вычислить периметр куба, зная его площадь поверхности. Для этого нужно воспользоваться формулой, которая связывает площадь поверхности куба с его периметром: Периметр куба = √(Площадь поверхности куба/6).
Используя эти простые формулы, можно легко и быстро узнать периметр куба, что позволит решать задачи, связанные с этим геометрическим телом.
Куб: определение, свойства и простой способ расчета периметра
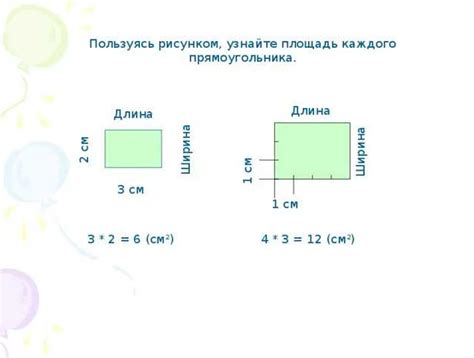
Периметр куба - это сумма длин всех его ребер. Мы можем вычислить периметр куба, используя простой способ. Для этого нужно знать длину одного ребра куба.
| Свойства | Значение |
|---|---|
| Количество граней | 6 |
| Количество ребер | 12 |
| Количество вершин | 8 |
Пусть a - длина ребра куба. Тогда периметр куба равен 12a, так как у куба 12 ребер одинаковой длины.
Пример расчета периметра куба:
Пусть длина ребра куба a = 5 см.
Тогда периметр куба равен 12 * 5 = 60 см.
Таким образом, периметр куба можно легко вычислить, зная длину одного из его ребер. Это простой и быстрый способ определить периметр куба.
Что такое куб и его основные характеристики
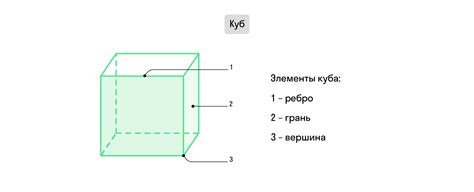
Основные характеристики куба следующие:
- Периметр. Периметр куба - это сумма длин всех его ребер. Для простого куба, где все ребра равны между собой, периметр можно вычислить, умножив длину одного ребра на 12.
- Площадь поверхности. Площадь поверхности куба - это сумма площадей всех его граней. Для простого куба, где все грани квадратные и равны между собой, площадь поверхности можно вычислить, умножив площадь одной грани на 6.
- Объем. Объем куба - это объем пространства, занимаемого им. Для простого куба, объем можно вычислить, возведя длину одного ребра в куб.
Куб - это одна из основных фигур в геометрии, часто используемая в математике, физике и других науках. Его простота и симметричность делают его удобным для изучения и расчетов. Понимание основных характеристик куба позволяет легко рассчитывать его периметр, площадь поверхности и объем, что полезно в различных практических применениях и задачах.
Формула расчета периметра куба
Периметр куба вычисляется по формуле:
| Периметр куба | = | длина ребра | × | количество ребер |
| = | a | × | 12 | |
| = | 12a |
Где а - длина ребра куба.
Таким образом, если известна длина ребра куба, чтобы найти его периметр, нужно умножить длину ребра на 12.
Примеры простого способа определения периметра куба
- Пример 1:
- Пример 2:
- Пример 3:
Допустим, мы знаем длину ребра куба, которая равна 5 см. Чтобы найти периметр куба, мы можем просто умножить длину ребра на 12, так как куб имеет 12 ребер.
Периметр куба = 5 см * 12 = 60 см
Предположим, что мы знаем общую площадь поверхности куба, которая составляет 150 см². Чтобы найти периметр куба, мы можем использовать формулу периметра куба, которая равна 4 * длина ребра куба.
Периметр куба = 4 * длина ребра куба
Так как все стороны куба равны, мы можем найти длину ребра куба, поделив общую площадь поверхности на 6 (площадь каждой грани куба).
150 см² / 6 = 25 см
Периметр куба = 4 * 25 см = 100 см
Допустим, мы знаем объем куба, который составляет 64 см³. Чтобы найти периметр куба, мы можем использовать формулу периметра куба, которая равна 12 * кубический корень из объема.
Периметр куба = 12 * кубический корень из 64 см³
Кубический корень из 64 см³ равен 4 см, поскольку 4 * 4 * 4 = 64.
Периметр куба = 12 * 4 см = 48 см
Это только несколько примеров простого способа определения периметра куба. Зная длину ребра, общую площадь поверхности или объем куба, вы можете легко найти его периметр.
Значение и применение периметра куба в реальной жизни

1. Геометрия: Периметр куба является одной из основных характеристик этой геометрической фигуры. Он позволяет определить общую длину всех его ребер и рассчитать объем куба. Кроме того, периметр используется в задачах на нахождение длины отрезка, проведенного по ребру куба.
2. Строительство: В строительстве концепция периметра куба применяется при проектировании и расчете объемов материалов, таких как бетон, кирпичи или деревянные блоки. Зная периметр куба, можно определить количество материала, необходимое для его построения, и оценить стоимость строительства.
3. Дизайн: В дизайне интерьера и архитектуре периметр куба может использоваться для создания геометрических композиций или планирования пространства. Например, периметр куба может быть использован для определения размера стола или шкафа, чтобы они могли эффективно вписаться в определенное пространство.
4. Техника: Периметр куба также может быть использован в технике и машиностроении. Например, при проектировании корпуса электронной техники или упаковке продуктов необходимо учитывать периметр куба для обеспечения правильной формы и размеров устройства или упаковки.
Все эти примеры демонстрируют, как периметр куба играет важную роль в различных областях нашей жизни. Поэтому понимание и умение рассчитывать периметр куба являются полезными навыками, которые могут быть применены в реальных ситуациях.