Проверка принадлежности точки кругу – одна из основных задач геометрии. Но как это сделать? Существует несколько способов, которые позволяют определить, лежит ли точка внутри круга или снаружи его. Один из самых распространенных методов – использование формулы. Другие способы предлагаются графическим методом или с использованием треугольников.
Формула проверки принадлежности точки кругу основана на вычислении расстояния от данной точки до центра круга. С помощью этой формулы можно определить, находится ли точка внутри круга, на его границе или снаружи. Для этого необходимо знать координаты центра круга и радиус.
Графический метод основан на построении круга и отображении точки на графике. Если точка находится внутри круга или на его границе, то она будет находиться в его пределах. Если же точка находится вне круга, то она будет располагаться за его пределами. Этот метод позволяет быстро и наглядно определить принадлежность точки кругу.
Еще один способ основан на использовании свойств треугольников. Для этого требуется построить треугольник с вершинами в центре круга, точке искомой принадлежности и любой другой точке на границе круга. Затем необходимо вычислить площади треугольников, образованных заданными точками. Если сумма площадей этих треугольников равна площади треугольника, образованного вершинами в центре круга и на границе, то точка принадлежит кругу.
Способы проверки принадлежности точки кругу и формула для этого
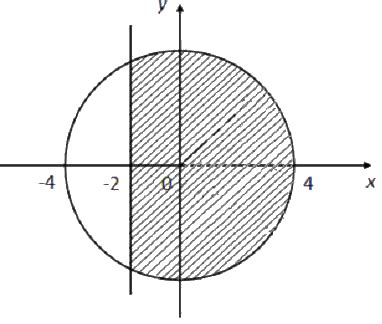
Сравнение расстояния от заданной точки до центра круга с радиусом: если расстояние меньше радиуса, то точка принадлежит кругу, если больше или равно радиусу, то не принадлежит.
Использование уравнения окружности: если уравнение окружности подставленное координаты точки удовлетворяют, то точка принадлежит кругу, в противном случае – нет.
Использование геометрических свойств, таких как теоремы Пифагора или использование определителя. Например, можно построить треугольник между центром круга, точкой и заданной точкой на окружности и проверить, соответствует ли его гипотенуза радиусу круга. Если да, то точка принадлежит кругу, если нет – не принадлежит.
Для проверки принадлежности точки кругу можно также использовать формулу:
Для круга с центром в точке (a, b) и радиусом r:
(x - a)^2 + (y - b)^2 ≤ r^2
Где (x, y) – координаты точки, которую нужно проверить.
Проверка на основе расстояния до центра круга

Другой способ узнать, принадлежит ли точка кругу, основан на анализе расстояния от точки до центра круга. Если расстояние между центром круга и точкой меньше или равно радиусу круга, то точка находится внутри круга.
| Шаги проверки на основе расстояния: |
|---|
| 1. Найдите координаты центра круга и запишите их. |
| 2. Найдите расстояние между центром круга и точкой с помощью формулы для расстояния между двумя точками на плоскости: √((x2 - x1)² + (y2 - y1)²), где (x1, y1) - координаты центра круга, (x2, y2) - координаты проверяемой точки. |
| 3. Сравните полученное расстояние с радиусом круга. |
| 4. Если расстояние меньше или равно радиусу круга, то точка находится внутри круга. Если расстояние больше радиуса круга, то точка находится вне круга. |
Проверка на основе расстояния до центра круга предоставляет удобный и наглядный способ определить, принадлежит ли точка кругу. С помощью данного метода можно проверить любое количество точек на принадлежность кругу.
Проверка на основе уравнения окружности
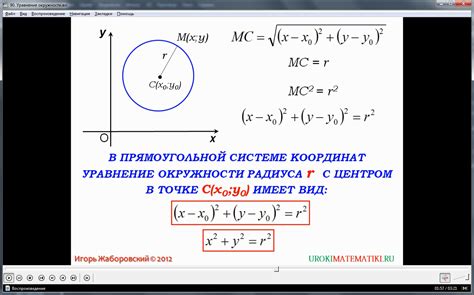
Существует формула, позволяющая проверить принадлежность точки кругу на основе уравнения окружности.
Уравнение окружности задается следующей формулой:
(x - a)² + (y - b)² = r²
Где:
- (x, y) - координаты точки
- (a, b) - координаты центра окружности
- r - радиус окружности
Для проверки принадлежности точки кругу необходимо подставить координаты точки в уравнение окружности. Если полученное значение равно или меньше радиуса окружности в квадрате, то точка принадлежит кругу. В противном случае, точка находится вне круга.
Таким образом, проверка принадлежности точки кругу на основе уравнения окружности – это сравнение значения уравнения окружности с квадратом радиуса окружности.
Геометрическая проверка на основе радиуса и координат точки
Для проверки принадлежности точки кругу можно использовать геометрический подход на основе радиуса и координат точки.
Для начала необходимо определить радиус круга. Радиус представляет собой расстояние от центра круга до любой его точки. Если радиус круга равен r, то уравнение окружности можно записать в виде:
(x - a)^2 + (y - b)^2 = r^2
где (a, b) - координаты центра круга, (x, y) - координаты точки.
Для проверки принадлежности точки кругу необходимо подставить координаты точки в данное уравнение и проверить, выполняется ли оно. Если равенство выполняется, то точка лежит на границе круга, а если неравенство выполняется, то точка находится внутри круга.
В данном методе важно учесть, что если точка находится вне круга, то радиус будет больше расстояния от центра круга до точки, а если точка находится внутри круга, то радиус будет меньше расстояния от центра круга до точки.
Таким образом, геометрическая проверка принадлежности точки кругу на основе радиуса и координат точки является эффективным и простым способом определения расположения точки относительно круга.
Аналитическая проверка с использованием уравнения окружности
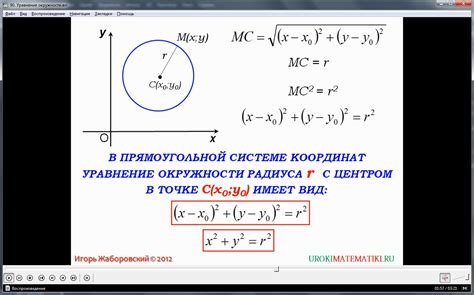
Для определения принадлежности точки кругу можно использовать уравнение окружности. Уравнение окружности удобно в использовании, когда известны координаты центра окружности и ее радиус.
Уравнение окружности имеет следующий вид:
| (x - a)^2 + (y - b)^2 = r^2 |
Где (x, y) - координаты точки, a и b - координаты центра окружности, r - радиус окружности.
Для проверки принадлежности точки кругу необходимо подставить ее координаты в уравнение окружности. Если результат равен нулю, то точка лежит на окружности. Если результат меньше нуля, то точка находится внутри окружности. Если результат больше нуля, то точка находится вне окружности.
Пример проверки принадлежности точки с координатами (3, 4) к окружности с центром в точке (2, 2) и радиусом 5:
| (3 - 2)^2 + (4 - 2)^2 = 1 + 4 = 5 |
Таким образом, точка (3, 4) находится на окружности, так как результат равен нулю.
Таким образом, аналитическая проверка с использованием уравнения окружности позволяет определить принадлежность точки кругу и является одним из эффективных способов для решения данной задачи.
Использование теоремы Пифагора для проверки принадлежности точки кругу

Для проверки принадлежности точки кругу можно использовать теорему Пифагора.
Формула теоремы Пифагора устанавливает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:
a^2 + b^2 = c^2
Когда точка задана своими координатами (x, y), можно вычислить расстояние от этой точки до центра круга (х0, у0) с помощью формулы:
d = sqrt((x - x0)^2 + (y - y0)^2)
где d - расстояние от точки до центра круга.
Если расстояние d меньше радиуса круга r, значит точка (x, y) принадлежит кругу.
Используя теорему Пифагора, можно с легкостью проверить принадлежность точки кругу, зная координаты точки и радиус круга.
Формула проверки принадлежности точки кругу по координатам и радиусу
Для проверки принадлежности точки кругу можно использовать математическую формулу, основанную на координатах точки и радиусе круга.
Формула проверки принадлежности точки к кругу выглядит следующим образом:
Если расстояние от центра круга до точки меньше или равно радиусу круга, то точка принадлежит кругу.
Математически эта формула записывается следующим образом:
√((x - cx)2 + (y - cy)2) ≤ r
Где:
- x - координата точки по оси X
- y - координата точки по оси Y
- cx - координата центра круга по оси X
- cy - координата центра круга по оси Y
- r - радиус круга
- √ - символ корня
Если значение выражения (x - cx)2 + (y - cy)2 больше, чем r2, то точка лежит за пределами круга.
Таким образом, по координатам точки и радиусу круга можно легко проверить принадлежность точки кругу, используя данную формулу.